a) Một phòng họp có tổng số 80 ghế ngồi, được xếp thành từng hàng, mỗi

Câu hỏi
Nhận biếta) Một phòng họp có tổng số 80 ghế ngồi, được xếp thành từng hàng, mỗi hàng có số lượng ghế bằng nhau. Nếu bớt đi 2 hàng mà không làm thay đổi số lượng ghế trong phòng thì mỗi hàng còn lại phải xếp thêm 2 ghế. Hỏi lúc đầu trong phòng có bao nhiêu hàng ghế?
b) Trên mặt phẳng tọa độ Oxy cho paradol (P): \(y=-{{x}^{2}}\)và đường thẳng \((d):y=x-2\) cắt nhau tại hai điểm A, B. Tìm tọa độ các điểm A, B và tính diện tích tam giác AOB (trong đó O là gốc tọa độ, hoành độ của điểm A lớn hơn hoành độ của điểm B).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Gọi số hàng ghế lúc đầu là x (\(x\in {{N}^{*}};x\ge 2;80\vdots x\)).
\(\Rightarrow \) Số ghế ở mỗi hàng lúc đầu là \(\frac{80}{x}\) (chiếc).
Nếu bớt đi 2 hàng thì số hàng còn lại là x – 2.
Khi đó, số ghế ở mỗi hàng là \(\frac{80}{x-2}\) (chiếc).
Vì lúc đó mỗi hàng còn lại phải xếp thêm 2 ghế nên ta có phương trình:
\(\begin{array}{l}
\frac{{80}}{{x - 2}} - \frac{{80}}{x} = 2 \Leftrightarrow 80x - 80\left( {x - 2} \right) = 2x\left( {x - 2} \right)\\
\Leftrightarrow {x^2} - 2x - 80 = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 10(tm)\\
x = - 8(ktm)
\end{array} \right.
\end{array}\)
Vậy lúc đầu có 10 hàng ghế.
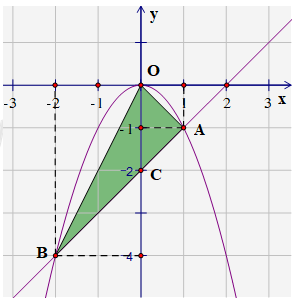
b) Xét phương trình hoành độ giao điểm của (P) và (d): \(-{{x}^{2}}=x-2\Leftrightarrow {{x}^{2}}+x-2=0\)
Vì a + b + c = 1 + 1 – 2 = 0 nên phương trình có hai nghiệm:\({{x}_{1}}=1,\,{{x}_{2}}=-2\)
Với x = 1 ⇒ y = 1 – 2 = – 1\(\Rightarrow \) A(1; – 1)
Với x = – 2 ⇒ y = – 2 – 2 = – 4 ⇒ B(– 2; – 4)
Dễ thấy (d) cắt Oy tại điểm C(0; – 2). Do đó:
\({{S}_{OAB}}={{S}_{OAC}}+{{S}_{OBC}}=\frac{2.1}{2}+\frac{2.2}{2}=3\) (đvdt).

