a) Một khu vườn hình chữ nhật có kích thước là 25m và 40m. Người ta tăng mỗi kích thước của khu
Câu hỏi
Nhận biếta) Một khu vườn hình chữ nhật có kích thước là 25m và 40m. Người ta tăng mỗi kích thước của khu vườn thêm x (mét). Gọi S và P theo thứ tự là diện tích và chu vi của khu vườn mới tính theo x. Hỏi các đại lượng S và P có phải là hàm số bậc nhất của x không? Vì sao? Tính giá trị của x khi biết giá trị tương ứng của P là 144 (tính theo đơn vị mét).
b) Cho hàm số y = -2x + 3 có đồ thị là (d1) và hàm số y = x có đồ thị là (d2). Vẽ (d1) và (d2) trên cùng mặt phẳng tọa độ Oxy. Tìm tọa độ giao điểm của (d1) và (d2) bằng phép tính.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
a)
Chiều rộng của khu vườn sau khi tăng thêm x(m) là: \(25 + x\) (mét)
Chiều dài của khu vườn sau khi tăng thêm x(m) là: \(40 + x\) (mét)
Chu vi của khu vườn mới là: \(P = \left( {25 + x + 40 + x} \right).2 = \left( {65 + 2x} \right).2 = 4x + {130^{}}\left( m \right)\)
Diện tích của khu vườn mới là: \(S = \left( {25 + x} \right).\left( {40 + x} \right) = {x^2} + 65x + {1000^{}}\left( {{m^2}} \right)\)
Do: \(P = 4x + 130\) có dạng \(y = ax + b\) với \(a = 4 \ne 0\), \(b = 130\) nên \(P = 4x + 130\) là hàm số bậc nhất.
Do: \(S = {x^2} + 65x + 1000\) không có dạng \(y = ax + b\) nên không phải là hàm số bậc nhất.
v Với P = 144 (m), thay vào \(P = 4x + 130\), ta được: \(144 = 4x + 130 \Leftrightarrow 4x = 14 \Leftrightarrow x = 3,5\left( m \right)\)
b)
Bảng giá trị:
Đồ thị:
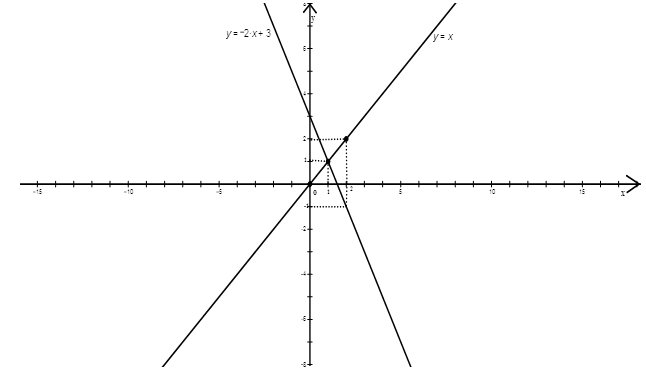
Phương trình hoành độ giao điểm của (d1) và (d2): \( - 2x + 3 = x \Leftrightarrow 3x = 3 \Leftrightarrow x = 1\)
Thay x = 1 vào (d2) \( \Rightarrow y = 1\)
Vậy: Tọa độ giao điểm của (d1) và (d2) là \(\left( {1{;^{}}1} \right)\).
