a) Hai điểm sáng S1 và S2 cùng nằm trên trục chính, nằm về hai phía củ
Câu hỏi
Nhận biếta) Hai điểm sáng S1 và S2 cùng nằm trên trục chính, nằm về hai phía của một thấu kính hội tụ, cách thấu kính lần lượt là 6cm và 12cm. Khi đó ảnh của S1 và ảnh của S2 tạo bởi thấu kính là trùng nhau. Hãy vẽ hình, giải thích sự tạo ảnh qua thấu kính. Từ đó tính tiêu cự của thấu kính (Không dùng công thức thấu kính).
b) Một điểm sáng A và màn ảnh (E) được đặt cách nhau một khoảng cố định a = 100cm.Đặt một thấu kính hội tụ (L) có rìa hình tròn, nằm trong khoảng giữa A và màn (E) sao cho trục chính của thấu kính vuông góc với màn, A nằm trên trục chính (Hình 2). Tịnh tiến thấu kính dọc theo trục chính trong khoảng giữa A và màn (E) người ta thấy trên màn thu được một vệt sáng, vệt sáng này không bao giờ thu lại thành một điểm. Khi thấu kính cách màn một đoạn b = 40cm thì vệt sáng trên màn có bán kính nhỏ nhất. Tính tiêu cự của thấu kính.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
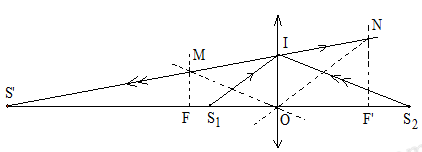
Giải thích sự tạo ảnh qua thấu kính:
+ Hai ảnh của S1 và của S2 tạo bởi thấu kính trùng nhau nên phải có một ảnh thật và một ảnh ảo.
+ Vì S1O < S2O S1 nằm trong khoảng tiêu cự và cho ảnh ảo; S2 nằm ngoài khoảng tiêu cự và cho ảnh thật
Tính tiêu cự của thấu kính:
+ Gọi S’ là ảnh của S1 và S2. Ta có:
\({S_1}I\,\,//\,ON \Rightarrow \Delta S'{S_1}I \sim \Delta S'ON\, \Rightarrow \frac{{S'{S_1}}}{{S'O}} = \frac{{S'I}}{{S'N}} \Rightarrow \frac{{S'O - 6}}{{S'O}} = \frac{{S'I}}{{{\rm{S'N}}}}\)
\(OI\,\,//\,\,NF' \Rightarrow \Delta S'OI \sim \Delta S'F'N \Rightarrow \frac{{S'O}}{{S'{\rm{F'}}}} = \frac{{S'I}}{{{\rm{S'N}}}}\)
\( \Rightarrow \frac{{S'O}}{{S'O + f}} = \frac{{S'I}}{{{\rm{S'N}}}} \Leftrightarrow \frac{{S'O - 6}}{{S'O}} = \frac{{S'O}}{{S'O + f}} \Rightarrow {\rm{f}}{\rm{.S'O = 6(S'O + f)}}\,\,\,\left( 1 \right)\)
\({\rm{FM // OI}} \Rightarrow \Delta S'FM \sim \Delta {S'}OI \Rightarrow \frac{{S'F}}{{S'O}} = \frac{{S'{\rm{M}}}}{{S'{\rm{I}}}}\)
\({{\rm{S}}_{\rm{2}}}{\rm{I // OM}} \Rightarrow \Delta S'OM \sim \Delta {S'}{S_2}I \Rightarrow \frac{{S'M}}{{S'I}} = \frac{{{{\rm{S}}^{\rm{'}}}O}}{{{{\rm{S}}^{\rm{'}}}{S_2}}}\)
Suy ra: \(\frac{{S'F}}{{S'O}} = \frac{{S'O}}{{{\rm{S'}}{{\rm{S}}_{\rm{2}}}}} \Leftrightarrow \frac{{S'O - f}}{{S'O}} = \frac{{S'O}}{{S'O + 12}} \Rightarrow {\rm{f}}{\rm{.S'O = 12(S'O - f)}}\,\,\left( 2 \right)\)
Từ (1) và (2) ta có: f = 8 (cm)
b)
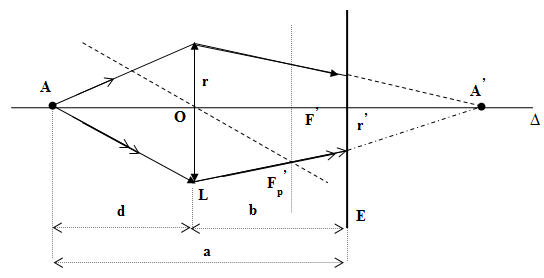
+ Sử dụng tính chất tam giác đồng dạng ta có:
\(\frac{{{r^,}}}{r} = \frac{{d' - b}}{{d'}} = 1 - a\left( {\frac{1}{f} - \frac{1}{d}} \right) + \left( {\frac{d}{f} - 1} \right) = \frac{a}{d} + \frac{d}{f} - \frac{a}{f}\)
với r: là bán kính đường tròn giới hạn thấu kính
r’: là bán kính đường tròn vết sáng
a: là khoảng cách từ điểm sáng A đến màn
b: là khoảng cách từ thấu kính đến màn
Theo bất đẳng thức Cô-si cho hai số:
\(\frac{a}{d} + \frac{d}{f} \ge 2\sqrt {\frac{a}{f}} \)
Vậy \(\frac{r}{{r'}}\) đạt giá trị cực tiểu khi: \(d = \sqrt {{\rm{af}}} = a - b\)
Do đó: \(\sqrt {{\rm{af}}} = a - b \Rightarrow f = \frac{{{{(100 - 40)}^2}}}{{100}} = 36cm\)









