(3,0 điểm) Cho mạch điện như hình vẽ. Hiệu điện thế giữa hai
Câu hỏi
Nhận biết(3,0 điểm)
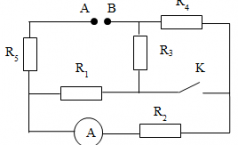
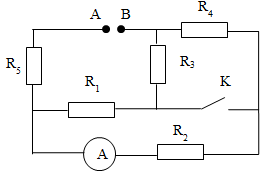
Cho mạch điện như hình vẽ. Hiệu điện thế giữa hai điểm A và B là 20V luôn không đổi. Biết R1 = 3Ω, R2 = R4 = R5 = 2Ω, R3 = 1Ω. Điện trở của ampe kế và dây nối không đáng kể.
1) Khi khoá K mở. Tính:
a) Điện trở tương đương của cả mạch.
b) Số chỉ của ampe kế và nhiệt lượng toả ra trên R3 trong thời gian 10 phút.
2) Thay điện trở R2 và R4 lần lượt bằng điện trở Rx và Ry, khi khoá K đóng và mở ampe kế đều chỉ 1A. Tính giá trị của điện trở Rx và Ry trong trường hợp này.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) Khi K mở ta có mạch sau : {(R1 nt R3) // (R2 nt R4)}
a) Điện trở R13 : R13 = R1 + R3 = 3 + 1 = 4Ω
Điện trở R24: R24 = R2 + R4 = 2 + 2 = 4Ω
Điện trở R1234: \({R_{1234}} = {{{R_{13}}{R_{24}}} \over {{R_{13}} + {R_{24}}}} = {{4.4} \over {4 + 4}} = 2\Omega \)
Điện trở tương đương cả mạch: RAB = R5 + R1234 = 2 + 2 = 4Ω
b) Cường độ dòng điện qua đoạn mạch AB: \(I = {U \over {{R_{AB}}}} = {{20} \over 4} = 5A\)
Vì R5 nt R1234 nên I5 = I1234 = 5A
Hiệu điện thế đoạn mạch mắc song song: U1234 = I.R1234 = 5.2 = 10V
Vì R13 // R24 nên U13 = U24 = U1234 = 10V
Cường độ dòng điện qua R24: I24 = U24/R24 = 10/4 = 2,5A
Số chỉ của ampe kế: IA = I24 = 2,5A
Cường độ dòng điện qua R13: I13 = I – I24 = 2,5A = I3
Nhiệt lượng toả ra trên R3 trong 10 phút = 600s: \({Q_3} = I_3^2.{R_3}.t = {2,5^2}.1.600 = 3750J\)
2) Khi K mở ta có mạch sau: R5 nt [(R1 nt R3) // (Rx nt Ry)]
Cường độ dòng điện qua cả mạch:
\(I = {U \over {{R_5} + {{({R_1} + {R_3}).({R_x} + {R_y})} \over {{R_1} + {R_3} + {R_x} + {R_y}}}}} = {{20} \over {2 + {{4.({R_x} + {R_y})} \over {4 + {R_x} + {R_y}}}}} = {{10.(4 + {R_x} + {R_y})} \over {(4 + {R_x} + {R_y}) + 2.({R_x} + {R_y})}}(1)\)
Vì R13 // Rxy nên: \({{{I_A}} \over I} = {{{R_1} + {R_3}} \over {{R_1} + {R_3} + {R_x} + {R_y}}}\) hay \({1 \over I} = {4 \over {4 + {R_x} + {R_y}}} \Rightarrow I = {{4 + {R_x} + {R_y}} \over 4}(2)\)
Từ (1) và (2) suy ra: \({{4 + {R_x} + {R_y}} \over 4} = {{10.(4 + {R_x} + {R_y})} \over {(4 + {R_x} + {R_y}) + 2.({R_x} + {R_y})}}\)
Biến đổi => Rx + Ry = 12Ω (3)
Từ (3) => 0 < Rx; Ry < 12 (4)
Khi K đóng: R5 nt (R1 // Rx) nt (R3 // Ry)
Cường độ dòng điện trong mạch chính:
\(\eqalign{ & I' = {{20} \over {{R_5} + {{{R_1}.{R_x}} \over {{R_1} + {R_x}}} + {{{R_3}.{R_y}} \over {{R_3} + {R_y}}}}} = {{20} \over {2 + {{3{R_x}} \over {3 + {R_x}}} + {{{R_y}} \over {1 + {R_y}}}}} = {{20} \over {2 + {{3{R_x}} \over {3 + {R_x}}} + {{12 - {R_x}} \over {13 - {R_x}}}}} \cr & I' = {{20.(3 + {R_x})(13 - {R_x})} \over {2.(3 + {R_x})(13 - {R_x}) + 3{R_x}.(13 - {R_x}) + (12 - {R_x})(3 + {R_x})}}(5) \cr} \)
Vì R1 // Rx nên: \({{{I_A}} \over {I'}} = {{{R_1}} \over {{R_1} + {R_x}}}\)
\({1 \over {I'}} = {3 \over {3 + {R_x}}}\)
hay \(I' = {{3 + {R_x}} \over 3}\) (6)
Từ (5) và (6) suy ra:
\(\eqalign{ & {{3 + {R_x}} \over 3} = {{20.(3 + {R_x})(13 - {R_x})} \over {2.(3 + {R_x})(13 - {R_x}) + 3{R_x}(13 - {R_x}) + (12 - {R_x})(3 + {R_x})}} \cr & \Leftrightarrow 2R_x^2 - 128{R_x} + 666 = 0 \cr} \)
Giải phương trình bậc hai ta được hai nghiệm: Rx1 = 12,33; Rx2 = 9
Theo điều kiện (4) ta loại Rx1 nhận Rx2 = 9 Ω
Suy ra Ry = 12 – Rx = 12 – 9 = 3Ω
Vậy Rx = 9Ω; Ry = 3Ω
