(2,0 điểm) Một điểm sáng S nằm trên trục chính của thấu kín
Câu hỏi
Nhận biết(2,0 điểm)
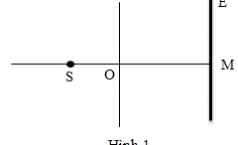
Một điểm sáng S nằm trên trục chính của thấu kính O, màn E đặt vuông góc với trục chính tại M. Thấu kính và màn được giữ cố định với khoảng cách OM = 40cm (hình 1).

1) Khi SO = 20cm thì kích thước vệt sáng trên màn bằng kích thước thấu kính. Tìm tiêu cự của thấu kính.
2) Điều chỉnh SO = 30cm rồi đánh dấu kích thước vệt sáng trên màn. Nếu di chuyển S trên trục chính của thấu kính một đoạn là x thì vệt sáng trên màn lại có kích thước như cũ. Tìm x và chiều di chuyển của S.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
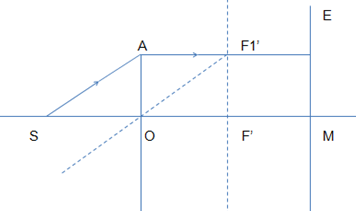
1) Tứ giác SAF1’O là hình bình hành SO = AF1’ (1)
Tứ giác AF1’F’O là hình vuông => AF1’ = OF’ (2)
Từ (1) và (2) suy ra OF’ = SO = 20cm
Vậy tiêu cự của thấu kính là f = 20cm
2) Giả thiết: OS1 = 30 cm; OS2 = 30 + x (cm); MA1 = MA2
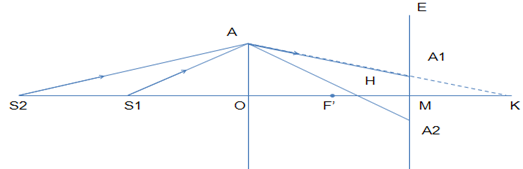
Ta có: \(OK = {{O{S_1}.f} \over {O{S_1} - f}} = 60cm\)
Do A1M là đường trung bình của tam giác KOA nên: \({{{A_1}M} \over {OA}} = {{KM} \over {OK}} = {{OK - OM} \over {OK}} = {{60 - 40} \over {60}} = {2 \over 3}\) (3)
Lại có: \(OH = {{O{S_2}.f} \over {O{S_2} - f}} = {{(30 + x).20} \over {10 + x}} \Rightarrow HM = OM - OH = 40 - {{(30 + x).20} \over {10 + x}} = {{20x - 200} \over {10 + x}}\)
Do: \(\Delta AOH \sim \Delta {A_2}MH \Rightarrow {{M{A_2}} \over {OA}} = {{HM} \over {OH}} = {{20x - 200} \over {(30 + x).20}} = {{x - 10} \over {30 + x}}\) (4)
Từ (3) và (4) ta được: \({{x - 10} \over {30 + x}} = {2 \over 3} \Leftrightarrow x = 90cm\)
Chiều di chuyển của S là chiều ra xa thấu kính đổi









