1. Một con thuyền ở địa điểm D di chuyển từ bờ sông a sang bờ sông b v

Lời giải của Tự Học 365

Giải chi tiết:

1. Tính chiều rộng khúc sông.

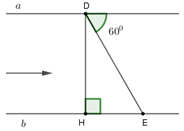
Kẻ \(DH \bot b\) tại \(H.\) Khi đó chiều rộng khúc sông là đoạn \(DH.\)

Đổi \(20\) phút \( = \frac{1}{3}h.\)

Độ dài đường đi của thuyền là \(DE = \frac{1}{3}.2 = \frac{2}{3}km\)

Ta có \(\angle HDE = {90^0} - {60^0} = {30^0}\)

Xét tam giác \(DHE\) vuông tại \(H\), theo định nghĩa tỉ số lượng giác ta có:

 \(\cos \angle HDE = \frac{{DH}}{{DE}} \Rightarrow DH = DE.\cos {30^0} = \frac{2}{3}.\frac{{\sqrt 3 }}{2} = \frac{{\sqrt 3 }}{3}\)

Vậy chiều rộng khúc sông là \(\frac{{\sqrt 3 }}{3}\,km.\)

2. Lấy điểm \(A\) trên \(\left( {O;R} \right),\) vẽ tiếp tuyến \(Ax.\) Trên \(Ax\) lấy điểm \(B,\) trên \(\left( {O;R} \right)\) lấy điểm \(C\) sao cho \(BC = AB.\)  

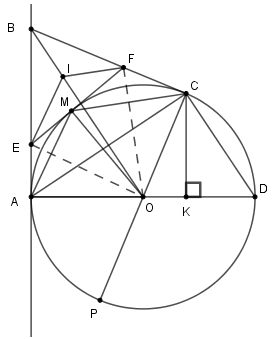
a) Chứng minh rằng : \(CB\) là tiếp tuyến của \(\left( O \right).\)

Xét \(\Delta ABO\) và \(\Delta CBO\) có:

+) \(AB = BC\left( {gt} \right)\)

+) \(BO\) cạnh chung

+) \(OA = OC\left( { = R} \right)\)

Nên \(\Delta ABO = \Delta CBO\left( {c - c - c} \right)\)

Suy ra \(\angle BCO = \angle BAO = {90^0}\), do đó: \(BC \bot OC\) tại \(C\).

Hay \(BC\) là tiếp tuyến của \(\left( {O;R} \right).\)

b) Vẽ đường kính \(AD\) của \(\left( O \right),\) kẻ \(CK\) vuông góc với \(AD.\)

Chứng minh rằng : \(CD//OB\) và \(BC.DC = CK.OB.\)

*) Xét đường tròn \(\left( {O;R} \right)\) có \(\Delta ACD\) nội tiếp đường tròn có cạnh \(AD\) là đường kính nên \(\Delta ACD\) vuông tại \(C.\)

Hay \(AC \bot CD\).

+) Xét đường tròn \(\left( {O;R} \right)\) có \(BA,BC\) là các tiếp tuyến cắt nhau tại \(B\) nên \(BA = BC\) (tính chất hai tiếp tuyến cắt nhau)

Suy ra \(B\) thuộc đường trung trực của đoạn \(AC.\)

Lại có \(OA = OC = R\) nên \(O\) thuộc đường trung trực của đoạn \(AC.\)

Từ đó \(OB\) là đường trung trực của đoạn \(AC \Rightarrow OB \bot AC.\)

Lại có \(AC \bot CD\left( {cmt} \right)\) nên \(OB//CD.\)

*) Xét \(\Delta CKD\) và \(\Delta BAO\) có:

+)  \(\angle K = \angle BAO = {90^0}\)

+) \(\angle CDK = \angle AOB\) (hai góc ở vị trí đồng vị)

Nên \(\Delta CDK\) đồng dạng với \(\Delta BAO\,\,\,\left( {g - g} \right)\)

Suy ra \(\frac{{CK}}{{AB}} = \frac{{DC}}{{OB}} \Leftrightarrow OB.CK = DC.AB\)

Mà \(AB = BC\) (gt) nên \(OB.CK = BC.DC\) (đpcm)

c) Lấy \(M\) trên cung nhỏ \(AC\) của \(\left( O \right),\) vẽ tiếp tuyến tại \(M\)cắt \(AB,\,BC\) lần lượt tại  \(E,\,\,F.\) Vẽ đường tròn tâm \(I\) nội tiếp tam giác \(BFE.\) Chứng minh rằng : \(\Delta MAC \sim \Delta \,IFE.\)

Kẻ đường kính \(CP\) của \(\left( {O;R} \right)\)

Ta có:  \(\angle POA\) là góc ngoài của tam giác \(OAC\) nên \(\angle POA = \angle OCA + \angle OAC\) mà \(\angle OAC = \angle OCA\) (do tam giác \(OCA\) cân tại \(O\)) nên \(\angle POA = 2\angle ACO.\)

Lại có \(\angle POM\) là góc ngoài của tam giác \(OCM\) nên \(\angle POM = \angle OCM + \angle OMC\) mà \(\angle OCM = \angle OMC\) (do tam giác \(OCM\) cân tại \(O\)) nên \(\angle POM = 2\angle MCO.\)

Do đó:  \(\angle POM - \angle POA = 2\left( {\angle MCO - \angle ACO} \right)\) hay \(\angle MOA = 2\angle MCA.\)

Xét tứ giác \(EMOA\) có \(\angle EAO = \angle EMO = {90^0}\) (tính chất tiếp tuyến)

Nên \(\angle MOA + \angle AEM = {360^0} - \left( {\angle EAO + \angle EMO} \right) = {180^0}\)

Mà \(\angle AEM + \angle BEF = {180^0}\) (hai góc kề bù)

Nên \(\angle MOA = \angle BEF\) (cùng bù với \(\angle AEM\))

Lại có \(\angle BEF = 2\angle IEF\) (do \(I\) là tâm đường tròn nội tiếp tam giác \(BEF\))

Và \(\angle MOA = 2\angle MCA\) (cmt)

Suy ra \(\angle IEF = \angle MCA\)

Chứng minh tương tự:

Ta có \(\angle DOM\) là góc ngoài của tam giác cân \(AOM \Rightarrow \angle DOM = 2\angle MAO\)

\(\angle DOC\) là góc ngoài của tam giác cân \(AOC \Rightarrow \angle DOC = 2\angle CAO\)

Trừ vế với vế ta được: \(\angle MOC = 2\angle MAC\)

Lại có \(\angle MFC + \angle MOC = {360^0} - \left( {\angle FMO - \angle CFO} \right) = {180^0}\)

Và \(\angle MFC + \angle BFE = {180^0} \Rightarrow \angle BFE = \angle COM\)

Mà \(\angle COM = 2\angle MAC;\,\,\,\,\angle BFE = 2\angle IFE\) nên \(\angle IFE = \angle MAC\)

Xét tam giác \(IEF\) và tam giác \(MCA\) có:  \(\angle IFE = \angle MAC\) và \(\angle IEF = \angle MCA\) (cmt) nên \(\Delta IEF\) đồng dạng với \(\Delta MCA\)(đpcm).