1. Cho tam giác ABC vuông tại A đường cao AH biết AB=5cm và BC=13cm . Từ H kẻ HK vuông góc với

Câu hỏi
Nhận biết1. Cho tam giác ABC vuông tại A, đường cao AH, biết \( AB=5cm\) và \( BC=13cm\) . Từ H kẻ \( HK\) vuông góc với AB \( \left( K\in AB \right)\) . Tính AC, BH và \( \cos \angle HBK\) .
2. Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn tâm O, các đường cao AD, BE cắt nhau tại H và cắt đường tròn (O) lần lượt tại I và K. (I khác A, K khác B)
a) Chứng minh tứ giác CDHE nội tiếp.
b) Chứng minh tam giác CKI cân.
c) Kẻ đường kính BF của đường tròn (O). Gọi P là trung điểm của AC. Chứng minh ba điểm H, P, F thẳng hàng.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
1.
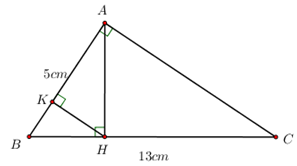
Áp dụng định lí Pitago trong tam giác ABC có: \( A{{B}^{2}}+A{{C}^{2}}=B{{C}^{2}}\Rightarrow {{5}^{2}}+A{{C}^{2}}={{13}^{2}}\Rightarrow A{{C}^{2}}=144\Rightarrow AC=12\,\,\left( cm \right)\) .
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
\( A{{B}^{2}}=BH.BC\Rightarrow BH=\frac{A{{B}^{2}}}{BC}=\frac{{{5}^{2}}}{13}=\frac{25}{13}\,\,\left( cm \right)\)
Xét tam giác vuông ABH có: \( \cos \angle HBK=\cos \angle HBA=\frac{BH}{AB}=\frac{\frac{25}{13}}{5}=\frac{5}{13}\) .
2. a) Chứng minh tứ giác CDHE nội tiếp.
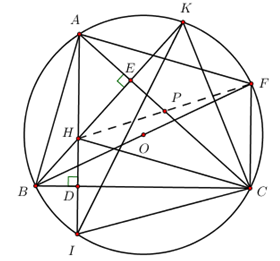
Xét tứ giác CDHE có: \(\angle CDH+\angle CEH={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow \) Tứ giác CDHE nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh tam giác CKI cân.
Ta có \( \Delta ACD\) vuông tại D \( \Rightarrow \angle CAD+\angle ACD={{90}^{0}}\Rightarrow \angle CAD={{90}^{0}}-\angle ACD\Rightarrow \angle CAI={{90}^{0}}-\angle ACB\)
\( \Delta BCE\) vuông tại E \( \Rightarrow \angle EBC+\angle ECB={{90}^{0}}\Rightarrow \angle EBC={{90}^{0}}-\angle ECB\Rightarrow \angle KBC={{90}^{0}}-\angle ACB\)
\( \Rightarrow \angle CAI=\angle KBC\)
Mà \( \angle CAI=\angle CKI\) (hai góc nội tiếp cùng chắn cung CI)
\( \angle KBC=\angle KIC\) (hai góc nội tiếp cùng chắn cung KC)
\( \Rightarrow \angle CKI=\angle KIC\Rightarrow \Delta CKI\) cân tại C.
c) Kẻ đường kính BF của đường tròn (O). Gọi P là trung điểm của AC. Chứng minh ba điểm H, P, F thẳng hàng.
H là trực tâm của tam giác ABC \( \Rightarrow CH\bot AB\) .
Ta có \( \angle BCF={{90}^{0}}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow CF\bot BC\Rightarrow CF//AH\)
Tương tự \( \angle BAF={{90}^{0}}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AF\bot AB\Rightarrow AF//CH\)
\( \Rightarrow \) Tứ giác AFCH là hình bình hành (dhnb)
\( \Rightarrow \) Hai đường chéo AC và HF cắt nhau tại trung điểm mỗi đường (Tính chất hình bình hành).
Mà P là trung điểm của AC (gt) \( \Rightarrow P\) là trung điểm của HF.
Vậy H, P, F thẳng hàng.
Chọn B

