1) Cho parabol ( P ): y=x^2 và đường thẳng ( d ): y=-x+2. a) Vẽ ( d

Câu hỏi
Nhận biết1) Cho parabol \( \left( P \right): \ y={{x}^{2}} \) và đường thẳng \( \left( d \right): \ y=-x+2. \)
a) Vẽ \( \left( d \right) \) và \( \left( P \right) \) trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của parabol \( \left( P \right) \) và đường thẳng \( \left( d \right) \) bằng phép tính.
2) Không sử dụng máy tính, giải hệ phương trình sau: \( \left \{ \begin{align} & 3x+y=5 \ \ & 2x-y=10 \ \ \end{align} \right.. \)
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
1) Cho parabol \(\left( P \right):\ \ y={{x}^{2}}\) và đường thẳng \(\left( d \right):\ \ y=-x+2.\)
a) Vẽ \(\left( d \right)\) và \(\left( P \right)\) trên cùng một mặt phẳng tọa độ Oxy.
+) Vẽ đồ thị hàm số:

+) Vẽ đồ thị hàm số:

Đồ thị hàm số:
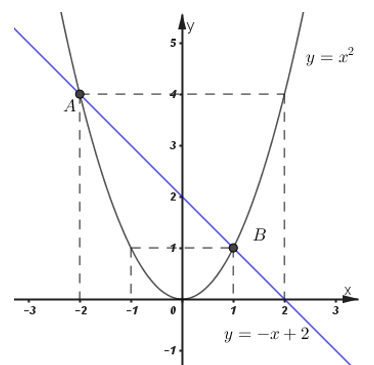
b) Tìm tọa độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \(\left( d \right)\) bằng phép tính.
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình hoành độ giao điểm.
Ta có phương trình hoành độ giao điểm của hai đồ thị là:
\(\begin{array}{l}
\;\;\; - x + 2 = {x^2}\\
\Leftrightarrow {x^2} + x - 2 = 0\\
\Leftrightarrow {x^2} + 2x - x - 2 = 0\\
\Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\
\Leftrightarrow \left( {x + 2} \right)\left( {x - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x + 2 = 0\\
x - 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = - 2 \Rightarrow y = 4\\
x = 1 \Rightarrow y = 1
\end{array} \right..
\end{array}\)
Vậy hai đồ thị cắt nhau tại hai điểm phân biệt \(A\left( -2;\ 4 \right)\) và \(B\left( 1;\ 1 \right).\)
2) Không sử dụng máy tính, giải hệ phương trình sau: \(\left\{ \begin{array}{l}
3x + y = 5\\
2x - y = 10
\end{array} \right..\)
\(\left\{ \begin{array}{l}
3x + y = 5\\
2x - y = 10
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
y = 2x - 10\\
5x = 15
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 3\\
y = 2.3 - 10
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 3\\
y = - 4
\end{array} \right..\)
Vậy hệ phương trình có nghiệm duy nhất: \(\left( x;\ y \right)=\left( 3;-4 \right).\)
Chọn B

