1) Cho nửa đường tròn ( O;R ) đường kính AB. Trên cùng nửa mặt phẳng b

Câu hỏi
Nhận biết1) Cho nửa đường tròn \(\left( {O;R} \right)\) đường kính \(AB\). Trên cùng nửa mặt phẳng bờ \(AB\) chứa nửa đường tròn \(\left( {O;R} \right)\) vẽ các tiếp tuyến \(Ax,\,\,By\) với nửa đường tròn đó. Gọi \(M\) là một điểm bất kì trên nửa đường tròn \(\left( {O;R} \right)\) (với \(M\) khác \(A\), \(M\) khác \(B\)), tiếp tuyến của nửa đường tròn tại \(M\)cắt \(Ax,\,\,By\) lần lượt tại \(C\) và \(D\).
a) Chứng minh tứ giác \(ACMO\) nội tiếp.
b) Chứng minh tam giác \(COD\) vuông tại \(O\).
c) Chứng minh \(AC.BD = {R^2}\).
d) Kẻ \(MN \bot AB\,\,\left( {N \in AB} \right)\); \(BC\) cắt \(MN\) tại \(I\). Chứng minh \(I\) là trung điểm của \(MN\).
2) Tính thể tích của một hình nón có bán kính đáy \(r = 4cm\), độ dài đường sinh \(l = 5cm\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
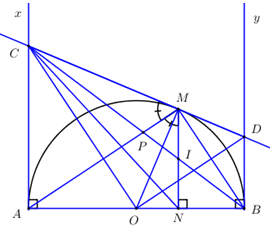
1) a) Chứng minh tứ giác \(ACMO\) nội tiếp.
Do \(AC\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A \Rightarrow \angle OAC = {90^0}\).
\(MC\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(M \Rightarrow \angle OMC = {90^0}\).
Xét tứ giác \(ACMO\) có: \(\angle OAC + \angle OMC = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(ACMO\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Chứng minh tam giác \(COD\) vuông tại \(O\).
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có:
\(OC\) là tia phân giác của \(\angle AOM\);
\(OD\) là tia phân giác của \(\angle BOM\);
Mà \(\angle AOM;\,\,\angle BOM\) là hai góc kề bù \( \Rightarrow OC \bot OD\) (hai tia phân giác của 2 góc kề bù vuông góc với nhau).
\( \Rightarrow \angle COD = {90^0}\) hay tam giác \(COD\) vuông tại \(O\). (đpcm)
c) Chứng minh \(AC.BD = {R^2}\).
Áp dụng hệ thức lượng trong tam giác vuông \(OCD\) vuông tại \(O\) có đường cao \(OM\) ta có: \(O{M^2} = MC.MD\).
Mà \(OM = R \Rightarrow MC.MD = {R^2}\) (1).
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có: \(AC = MC;\,\,BD = MD\) (2).
Từ (1) và (2) suy ra \(AC.BD = {R^2}\). (đpcm)
d) Kẻ \(MN \bot AB\,\,\left( {N \in AB} \right)\); \(BC\) cắt \(MN\) tại \(I\). Chứng minh \(I\) là trung điểm của \(MN\).
Ta có: \(\left\{ \begin{array}{l}AC \bot AB\\BD \bot AB\\MN \bot AB\end{array} \right.\,\,\left( {gt} \right) \Rightarrow AC//BD//MN\) (Từ vuông góc đến song song).
Gọi \(P = AM \cap CN\). Áp dụng định lí Ta-lét ta có : \(\frac{{MI}}{{AC}} = \frac{{PI}}{{PC}};\,\,\frac{{NI}}{{AC}} = \frac{{BI}}{{BC}}\) (3).
Ta có : \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle AMN + \angle NMB = {90^0}\).
Mà trong tam giác vuông \(MNB\) lại có: \(\angle NBM + \angle NMB = {90^0}\)
\( \Rightarrow \angle AMN = \angle NBM = \angle ABM\).
Ta có : \(\angle ABM = \angle AMC\) (góc nội tiếp và tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AM\)) ;
\(\angle ABM = \angle AMN\) (cmt) ;
\( \Rightarrow \angle AMC = \angle AMN \Rightarrow MA\) là tia phân giác trong của góc \(CMN\).
Mà \(MB \bot MA\,\,\left( {\angle AMB = {{90}^0}} \right) \Rightarrow MB\) là tia phân giác ngoài của góc \(CMN\).
Áp dụng tính chất đường phân giác trong tam giác \(CMI\) ta có: \(\frac{{MI}}{{MC}} = \frac{{PI}}{{PC}} = \frac{{BI}}{{BC}}\) (4)
Từ (3) và (4) \( \Rightarrow \frac{{MI}}{{AC}} = \frac{{NI}}{{AC}} \Leftrightarrow MI = NI\).
Vậy \(I\) là trung điểm của \(MN\) (đpcm).
2) Chiều cao của hình nón là: \(h = \sqrt {{l^2} - {r^2}} = \sqrt {{5^2} - {4^2}} = \sqrt 9 = 3\,\,\left( {cm} \right).\)
Thể tích của hình nón đã cho là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.4^2}.3 = 16\pi \,\,\left( {c{m^3}} \right).\)

