1. Cho đường tròn tâm O và một điểm M nằm ngoài đường tròn. Từ M kẻ đư

Câu hỏi
Nhận biết1. Cho đường tròn tâm O và một điểm M nằm ngoài đường tròn. Từ M kẻ đường thẳng đi qua tâm O, cắt đường tròn tại hai điểm A, B (A nằm giữa M và B). Kẻ đường thẳng thứ hai đi qua M, cắt đường tròn tại hai điểm phân biệt C, D (C nằm giữa M và D, C khác A). Đường thẳng vuông góc với MA tại M cắt đường thẳng BC tại N, đường thẳng NA cắt đường tròn tại điểm thứ hai là E.
a) Chứng minh tứ giác AMNC là tứ giác nội tiếp.
b) Chứng minh DE vuông góc với MB.
2. Trên một khúc sông với 2 bờ song song với nhau , có một chiếc đò dự định chèo qua sông từ vị trí A ở bờ bên này sang vị trí B ở bờ bên kia, đường thẳng AB vuông góc với các bờ sông. Do bị dòng nước đẩy xiên nên chiếc đò đã cập bờ bên kia tại vị trí C cách B một khoảng bằng 30m. Biết khúc sông rộng 150m, hỏi dòng nước đã đẩy chiếc đò lệch đi một góc có số đo bằng bao nhiêu? (kết quả làm tròn đến giây)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1) a) Chứng minh tứ giác AMNC là tứ giác nội tiếp.
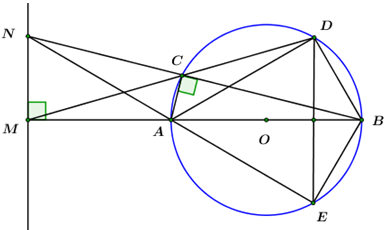
Ta có: \(MN \bot AB \Rightarrow \angle NMA = {90^0}\)
\(\angle ACB\) là góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)
\( \Rightarrow \angle ACB = \angle AMN = {90^0}\)
\( \Rightarrow AMNC\) là tứ giác nội tiếp (tứ giác có góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện).
b) Chứng minh DE vuông góc với MB.
Ta có tứ giác \(AMNC\) là tứ giác nội tiếp (cmt)
\( \Rightarrow \angle CNA = \angle CMA\) (hai góc nội tiếp cùng chắn cung \(AC\)).
Hay \(\angle BNE = \angle BMD.\) (1)
Xét đường tròn \(\left( O \right)\) ta có:
\(\angle BNE\) là góc có đỉnh nằm ngoài đường tròn chắn cung \(AC\) và \(BE.\)
\( \Rightarrow \angle BNE = \frac{1}{2}\left( {sd\,\,cung\,\,BE - sd\,\,cung\,\,\,AC} \right)\) (2)
\(\angle DMB\) là góc có đỉnh nằm ngoài đường tròn chắn cung \(AC\) và \(BD.\)
\( \Rightarrow \angle DMB = \frac{1}{2}\left( {sd\,\,cung\,\,BD - sd\,\,cung\,\,\,AC} \right)\) (3)
Từ (1), (2) và (3) suy ra: \(sd\,\,cung\,\,BD = sd\,\,\,cung\,\,\,BE\)
\( \Rightarrow BD = BE\) (hai cung bằng nhau căng hai dây bằng nhau).
\( \Rightarrow B\) nằm trên đường trung trực của \(DE.\) (4)
Lại có: \(\angle ADB = \angle AEB = {90^0}\) (các góc nội tiếp chắn nửa đường tròn \(\left( O \right)\)
Xét \(\Delta ADB\) và \(\Delta AEB\) ta có:
\(\begin{array}{l}\angle ADB = \angle AEB = {90^0}\,\,\,\,\left( {cmt} \right)\\\,\,AB\,\,\,chung\\\,\,DB = BE\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta ADB = \Delta AEB\,\,\,\left( {ch - cgv} \right)\end{array}\)
\( \Rightarrow AD = AE\) (hai cạnh tương ứng).
\( \Rightarrow A\) nằm trên đường trung trực của \(DE.\) (5)
Từ (4) và (5) \( \Rightarrow AB\) là đường trung trực của \(DE.\)
\( \Rightarrow AB \bot DE\,\,\,hay\,\,\,MB \bot DE\,\,\,\left( {dpcm} \right).\)
2) Ta có hình vẽ:

Ta có: \(AB \bot BC \Rightarrow \Delta ABC\) vuông tại B.
Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông ABC ta có:
\(\tan \,ACB = \frac{{AB}}{{BC}} = \frac{{150}}{{30}} = 5 \Rightarrow \angle ACB = {78^0}41'24''\)
Vậy dòng nước đã đẩy chiếc đò lệch đi một góc có số đo bằng \({90^0} - {78^0}41'24'' = {11^0}18'36''\) .

