Ví dụ minh họa bài toàn về độ lệch pha

VÍ DỤ MINH HỌA
|
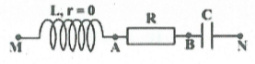
Bài tập minh họa: Cho vào mạch điện hình bên một dòng điện xoay chiều có cường độ $i={{I}_{0}}\cos 100\pi t\left( A \right)$. Khi đó ${{u}_{MB}}$ và ${{u}_{AN}}$ vuông pha nhau, và ${{u}_{MB}}=100\sqrt{2}\cos \left( 100\pi t+\frac{\pi }{3} \right)\left( V \right)$. Hãy viết biểu thức ${{u}_{AN}}$ và tìm hệ số công suất của mạch MN. |
HD giải:
Do pha ban đầu của i bằng 0 nên ${{\varphi }_{MB}}={{\varphi }_{{{u}_{MB}}}}-{{\varphi }_{i}}=\frac{\pi }{3}-0=\frac{\pi }{3}\,rad.$
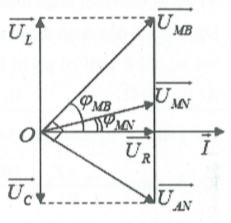
Dựa vào giản đồ vec-tơ, ta có các giá trị hiệu dụng của
${{U}_{L}},{{U}_{R}},{{U}_{C}}$ là:
${{U}_{R}}={{U}_{MB}}\cos {{\varphi }_{MB}}=\cos \frac{\pi }{3}=50\,V.$
${{U}_{L}}={{U}_{R}}\tan {{\varphi }_{MB}}=50\tan \frac{\pi }{3}=50\,\sqrt{3}V.$
Vì ${{u}_{MB}}$ và ${{u}_{AN}}$ vuông pha nhau nên
${{\varphi }_{MB}}-{{\varphi }_{AN}}=\frac{\pi }{2}\Rightarrow {{\varphi }_{AN}}=-\frac{\pi }{6}\,rad\Rightarrow \tan {{\varphi }_{MB}}.\tan {{\varphi }_{AN}}=-1$
$\Rightarrow \frac{{{U}_{L}}}{{{U}_{R}}}.\frac{-{{U}_{C}}}{{{U}_{R}}}=-1\Rightarrow {{U}_{C}}=\frac{U_{R}^{2}}{{{U}_{L}}}=\frac{{{50}^{2}}}{50\sqrt{3}}=\frac{50}{\sqrt{3}}V.$
Ta có: ${{U}_{AN}}=\frac{{{U}_{R}}}{\cos {{\varphi }_{AN}}}=\frac{50}{\cos \left( -\frac{\pi }{6} \right)}=\frac{100}{\sqrt{3}}\Rightarrow {{U}_{0AN}}=100\sqrt{\frac{2}{3}}V.$
Vậy biểu thức ${{u}_{AN}}=100\sqrt{\frac{2}{3}}\cos \left( 100\pi t-\frac{\pi }{6} \right)\left( V \right)$.
Hệ số công suất toàn mạch:
$\cos \varphi =\frac{R}{Z}=\frac{{{U}_{R}}}{U}=\frac{{{U}_{R}}}{\sqrt{U_{R}^{2}+{{\left( {{U}_{L}}-{{U}_{C}} \right)}^{2}}}}=\frac{50}{\sqrt{{{50}^{2}}+{{\left( 50\sqrt{3}-\frac{50}{\sqrt{3}} \right)}^{2}}}}=\sqrt{\frac{3}{7}}.$
VẬT LÝ LỚP 12