Tốc độ lực căng dây và năng lượng con lắc đơn (CLĐ) là gì

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1. Năng lượng của con lắc đơn

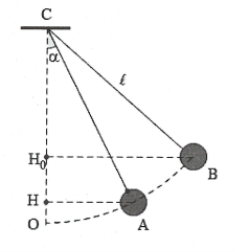
Chọn gốc thế năng ở vị trí cân bằng

Cơ năng:$\text{W}={{\text{W}}_{}}+{{\text{W}}_{t}}$

Thế năng trọng trường: ${{\text{W}}_{t}}=mgh$với $h=\ell \left( 1-c\text{os}\alpha \right).$

Động năng: ${{\text{W}}_{}}=\frac{1}{2}m{{v}^{2}}$

+) Tại vị trí biên B:

Thế năng cực đại: $\text{W}={{\text{W}}_{t\max }}=mg{{h}_{0}}$

$=mg\left( OC-C{{H}_{0}} \right)=mg\left( \ell -\ell \cos {{\alpha }_{0}} \right)$

$=mg\ell \left( 1-c\text{os}{{\alpha }_{0}} \right)$

+) Tại vị trí cân bằng O:

Động Năng cực đại: $\text{W}={{\text{W}}_{\max }}=\frac{mv_{\max }^{2}}{2}$ (${{v}_{\max }}$là vận tốc cực đại của vật).

+) Tại vị trí bất kì A: ${{\text{W}}_{A}}={{\text{W}}_{t}}\text{+}{{\text{W}}_{}}=mgh+\frac{m{{v}^{2}}}{2}$

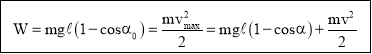Với $h=OC-HC=\ell \left( 1-c\text{os}\alpha \right)$, suy ra ${{\text{W}}_{A}}=mg\ell \left( 1-c\text{os}\alpha \right)+\frac{m{{v}^{2}}}{2}$

Cơ năng bảo toàn: (1)

Như vậy, suy ra ${{\text{W}}_{}}=mg\ell \left( \cos \alpha -\cos {{\alpha }_{0}} \right).$

2. Tốc độ, lực căng dây, gia tốc con lắc đơn

Tốc độ dao động con lắc đơn:

Ta có ${{\text{W}}_{}}=mg\ell \left( \cos \alpha -\cos {{\alpha }_{0}} \right)=\frac{1}{2}m{{v}^{2}}$suy ra

+) ${{v}_{\max }}=\sqrt{2g\ell \left( 1-\cos {{\alpha }_{0}} \right)}$tại VTCB $\left( \alpha =0 \right)$

+) ${{v}_{\min }}=0$tại hai biên $\left( \alpha =\pm {{\alpha }_{0}} \right)$.

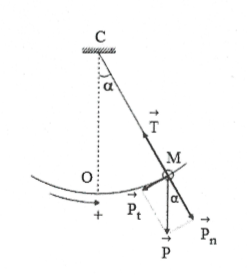
Lực căng dây $\overrightarrow{T}$:

Theo định luật II Niuton ta có:

$\overrightarrow{P}+\overrightarrow{T}=m\overrightarrow{a}$(*)

Chiếu (*) lên phương sợi dây ta có:

$P\cos \alpha +T=m{{a}_{ht}}\Rightarrow T=m\frac{{{v}^{2}}}{\ell }+mg\cos \alpha .$

Do $v=\sqrt{2g\ell \left( \cos \alpha -\cos {{\alpha }_{0}} \right)}$, suy ra

+) ${{T}_{\max }}=mg\left( 3-2\cos {{\alpha }_{0}} \right)$tại VTCB$\left( \alpha =0 \right)$

+) ${{T}_{\min }}=mg\cos {{\alpha }_{0}}$tại 2 biên $\left( \alpha =\pm {{\alpha }_{0}} \right)$

$\Rightarrow \frac{{{T}_{\max }}}{{{T}_{\min }}}=\frac{3-2\cos {{\alpha }_{0}}}{\cos {{\alpha }_{0}}}$

Lực kéo về của con lắc đơn:

$F=-mg\sin \alpha .$

Gia tốc của con lắc đơn:

Gia tốc của con lắc đơn được tính theo công thức: $a=\sqrt{a_{n}^{2}+a_{t}^{2}}$ với:

+) Thành phần pháp tuyến (gia tốc hướng tâm của vật):

${{a}_{n}}=\frac{{{v}^{2}}}{\ell }=2g\left( \cos \alpha -\cos {{\alpha }_{0}} \right).$

+) Thành phần tiếp tuyến của vật: ${{a}_{tt}}=-g\sin \alpha $

Khi vật dao động điều hòa: ${{a}_{tt}}=-g\alpha =-\frac{g}{\ell }.\ell \alpha =-{{\omega }^{2}}s.$

Tại vị trí cân bằng chỉ có gia tốc pháp tuyến, gia tốc tiếp tuyến bằng 0.

Tại vị trí biên vật chỉ có gia tốc tiếp tuyến, gia tốc pháp tuyến bằng 0 (vì vận tốc ở vị trí biên của vật bằng 0).

Trường hợp đặc biệt:

• Khi con lắc đơn dao động điều hòa (tức $sin\alpha \approx \alpha $) ta có:

$\text{W}={{\text{W}}_{t\max }}=mg{{h}_{0}}=mg\ell \left( 1-\cos {{\alpha }_{0}} \right)=mg\ell .2{{\left( \sin \frac{{{\alpha }_{0}}}{2} \right)}^{2}}\approx \frac{1}{2}mg\ell \alpha _{0}^{2}.$

Hoặc $\text{W}=\frac{mv_{\max }^{2}}{2}=\frac{m{{\omega }^{2}}{{s}^{2}}}{2}=\frac{m.\frac{g}{\ell }.{{\left( \ell {{\alpha }_{0}} \right)}^{2}}}{2}=\frac{1}{2}mg\ell \alpha _{0}^{2}$.

Vận tốc cực đại: ${{v}_{\max }}=\sqrt{2g\ell .2{{\sin }^{2}}\frac{{{\alpha }_{0}}}{2}}={{\alpha }_{0}}\sqrt{g\ell }={{\omega }^{2}}s.$

Tốc độc của vật: $v=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=\sqrt{\frac{g}{\ell }}\sqrt{{{\left( \ell {{\alpha }_{0}} \right)}^{2}}-{{\left( \ell \alpha \right)}^{2}}}=\sqrt{g\ell \left( \alpha _{0}^{2}-{{\alpha }^{2}} \right)}.$

Lực kéo về: $F=-mg\sin \alpha \approx -mg\alpha $

Hoặc: $F=-m{{\omega }^{2}}s=-m.\frac{g}{\ell }.s=-mg\alpha .$