Tích có hướng của 2 vecto là gì? Công thức, định nghĩa tính chất, ứng ụng

Tích có hướng của 2 vecto là gì? Công thức, định nghĩa tính chất, ứng ụng
1) Công thức định thức:
$\left| \begin{matrix} a {} b \\ c {} d \\\end{matrix} \right|=ad-bc.$
2) Định nghĩa tích có hướng của 2 vectơ:
Cho 2 vectơ: $\overrightarrow{u}=\left( {{x}_{1}};{{y}_{1}};{{z}_{1}} \right);\,\overrightarrow{v}=\left( {{x}_{2}};{{y}_{2}};{{z}_{2}} \right).$
Khi đó tích có hướng của 2 vectơ $\overrightarrow{u}=\left( {{x}_{1}};{{y}_{1}};{{z}_{1}} \right);\,\overrightarrow{v}=\left( {{x}_{2}};{{y}_{2}};{{z}_{2}} \right)$ký hiệu: $\left[ \overrightarrow{u},\overrightarrow{v} \right]$ là một vectơ và được tính như sau: $\left[ \overrightarrow{u},\overrightarrow{v} \right]=\left( \left| \begin{matrix} {{y}_{1}} {} {{z}_{1}} \\ {{y}_{2}} {} {{z}_{2}} \\\end{matrix} \right|;\left| \begin{matrix} {{z}_{1}} {} {{x}_{1}} \\ {{z}_{2}} {} {{x}_{2}} \\\end{matrix} \right|;\left| \begin{matrix} {{x}_{1}} {} {{y}_{1}} \\ {{x}_{2}} {} {{y}_{2}} \\\end{matrix} \right| \right)=\left( {{y}_{1}}{{z}_{2}}-{{y}_{2}}{{z}_{1}};{{z}_{1}}{{x}_{2}}-{{z}_{2}}{{x}_{1}};{{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}} \right)$
3) Tính chất:
$\left[ \overrightarrow{u},\overrightarrow{v} \right]\bot \overrightarrow{u};\,\,\left[ \overrightarrow{u},\overrightarrow{v} \right]\bot \overrightarrow{v};\,\,\left[ \overrightarrow{u},\overrightarrow{v} \right]=-\left[ \overrightarrow{v},\overrightarrow{u} \right]$
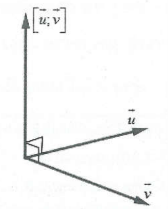
Độ dài của vectơ tích có hướng $\left| \left[ \overrightarrow{u},\overrightarrow{v} \right] \right|=\left| \overrightarrow{u} \right|.\left| \overrightarrow{v} \right|.\sin (\overrightarrow{u},\overrightarrow{v}).$
Hai vectơ $\overrightarrow{u};\,\,\overrightarrow{v}$ cùng phương $\Leftrightarrow \left[ \overrightarrow{u},\overrightarrow{v} \right]=\overrightarrow{0}\,\,(0;0;0).$
Ba vectơ $\overrightarrow{a};\,\,\overrightarrow{b};\,\,\overrightarrow{c}$ đồng phẳng khi $\left[ \overrightarrow{a},\overrightarrow{b} \right].\overrightarrow{c}=0.$
Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ $\overrightarrow{AB};\overrightarrow{\,AC};\overrightarrow{\,AD}$ không đồng phẳng hay $\left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD}\ne 0$ và 4 điểm A, B, C, D đồng phẳng khi $\left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD}=0.$
4) Ứng dụng:
- Diện tích hình bình hành $ABCD:\,\,\,{{S}_{ABCD}}=\left| \left[ \overrightarrow{AB},\overrightarrow{AD} \right] \right|.$
- Diện tích tam giác $ABC:\,\,\,{{S}_{ABC}}=\frac{1}{2}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right] \right|.$
- Thể tích khối hộp $ABCD.A'B'C'D':\,\,\,{{V}_{ABCD.A'B'C'D'}}=\left| \left[ \overrightarrow{AB},\overrightarrow{AD} \right].\overrightarrow{AA'} \right|.$
- Thể tích tứ diện ABCD: ${{V}_{ABCD}}=\frac{1}{6}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD} \right|.$
TOÁN LỚP 12
