Công Thức Tính Thể tích khối chỏm cầu - Ứng dụng tích phân

- Thể tích khối chỏm cầu
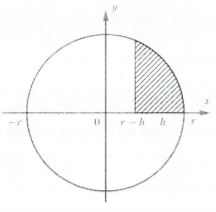
Khi quay hình phẳng tô đậm quanh trục $Ox$ ta được khối 3 chỏm cầu bán kính $r$ và chiều cao $h.$
Khi đó: ${{V}_{C}}=\pi \int\limits_{r-h}^{r}{{{\left( \sqrt{{{r}^{2}}-{{x}^{2}}} \right)}^{2}}dx}=\pi \int\limits_{r-h}^{r}{\left( {{r}^{2}}-{{x}^{2}} \right)dx}$
$\left. =\pi \left( \frac{{{r}^{2}}x}{3}-{{x}^{3}} \right) \right|_{r-h}^{r}=\pi {{h}^{2}}\left( r-\frac{h}{3} \right).$
- Thể tích khối nêm (xem hình vẽ)
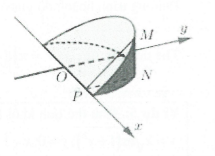
Đặt $OP=x;\,\,h=MN;\,\,\varphi =\widehat{MPN}\Rightarrow \tan \varphi =\frac{h}{R}\Rightarrow \left\{ \begin{matrix} NP=\sqrt{{{R}^{2}}-{{x}^{2}}} \\ MN=NP\tan \varphi \\\end{matrix} \right.$
$V=\int\limits_{-R}^{R}{S\left( x \right)dx}$ trong đó $S\left( x \right)=\frac{1}{2}MN.NP=\frac{1}{2}\left( {{R}^{2}}-{{x}^{2}} \right).\frac{h}{R}.$
$\Rightarrow V=\frac{1}{2}\int\limits_{-R}^{R}{\left( {{R}^{2}}-{{x}^{2}} \right).\frac{h}{R}}\,dx=\frac{1}{2}\frac{h}{R}.\left( 2{{R}^{3}}-\frac{2{{R}^{3}}}{3} \right)=\frac{2{{R}^{2}}h}{3}=\frac{2{{R}^{3}}\tan \varphi }{3}$
TOÁN LỚP 12
