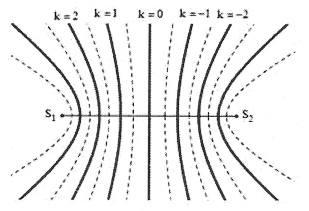
Quỹ tích cực đại cực tiểu giao thoa ánh sáng là gì?

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1) Hai nguồn cùng pha:

Cực đại: ${{d}_{2}}-{{d}_{1}}=k\lambda $.

+) Với $k=0\Rightarrow {{d}_{1}}={{d}_{2}}$: Quỹ tích các điểm cực đại trong trường hợp này là đường trung trực của AB.

+) Với $k=\pm 1\Rightarrow {{d}_{2}}-{{d}_{1}}=\pm \lambda $: Quỹ tích các điểm cực đại trong trường hợp này là đường cong Hypebol bậc 1, nhận A, B làm các tiêu điểm.

+) Với $k=\pm 2\Rightarrow {{d}_{2}}-{{d}_{1}}=\pm 2\lambda $: Quỹ tích các điểm cực đại trong trường hợp này là đường cong Hypebol bậc 2, nhận A, B làm các tiêu điểm… Tương tự với $k=3,4...$

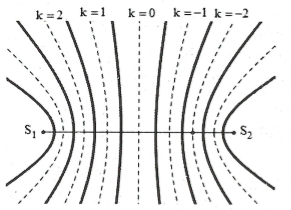Cực tiểu: ${{d}_{2}}-{{d}_{1}}=\left( k+0,5 \right)\lambda $

+) Với $k=0;k=-1\Rightarrow {{d}_{2}}-{{d}_{1}}=\pm \frac{\lambda }{2}$: Quỹ tích các điểm cực tiểu trong trường hợp này là đường cong Hypebol nhận A, B làm tiêu điểm, và nằm giữa đường trung trực của AB với đường cong Hypebol cực đại bậc 1.

+) Với $k=1;k=-2\Rightarrow {{d}_{2}}-{{d}_{1}}=\pm \frac{3\lambda }{2}$: Quỹ tích các điểm cực tiểu trong trường hợp này là đường cong Hypebol nhận A, B làm tiêu điểm, và nằm giữa đường Hypebol cực đại bậc 1 và cực đại bậc 2.

2) Hai nguồn ngược pha:

Các cực đại và cực tiểu ngược lại với trường hợp của hai nguồn cùng pha.

3) Hai nguồn lệch pha bất kỳ:

Ta có $\Delta \varphi ={{\varphi }_{1}}-{{\varphi }_{2}}+\frac{2\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }\xrightarrow{{}}\left\{ \begin{array}{} CD\text{:}{{\varphi }_{1}}-{{\varphi }_{2}}+\frac{2\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }=k2\pi \\ {} CT:{{\varphi }_{1}}-{{\varphi }_{2}}+\frac{2\pi \left( {{d}_{2}}-{{d}_{1}} \right)}{\lambda }=\left( 2k+1 \right)\pi \\ \end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}{} C\text{D}:{{d}_{2}}-{{d}_{1}}=k\lambda +\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{2\pi }\lambda \\ {} CT:{{d}_{2}}-{{d}_{1}}=\left( k+0,5 \right)\lambda +\frac{{{\varphi }_{2}}-{{\varphi }_{1}}}{2\pi }\lambda \\ \end{array} \right.$