Ôn tập định luật ôm cho toàn mạch - các loại đoạn mạch

VÁN ĐÈ 2: ĐỊNH LUẬT ÔM CHO TOÀN MẠCH. CÁC LOẠI ĐOẠN MẠCH.
DẠNG 1: ĐỊNH LUẬT ÔM CHO TOÀN MẠCH.
PHƯƠNG PHÁP GIẢI
1. Định luật Ôm toàn mạch: Cường độ dòng điện chạy trong mạch kín tỉ lệ thuận với suất điện động của nguồn điện và tỉ lệ nghịch với điện trở toàn phần của mạch đó:
$I=\frac{\xi }{{{R}_{N}}+r}$
Trong đó: $\xi $ (V) là suất điện động của nguồn
I (A) là cường độ dòng điện chạy trong mạch chính
r ($\Omega $ ) là điện trở trong của nguồn
${{R}_{N}}$ ($\Omega $ ) là tổng trở của mạch ngoài.
- Độ giảm thế: Tích của cường độ dòng điện chạy qua một đoạn mạch và điện trở của nó được gọi là độ giảm thế trên đoạn mạch đó. Suất điện động của nguồn điện có giá trị bằng tổng các độ giảm điện thế ở mạch ngoài và mạch trong:
$\xi =I.{{R}_{N}}+I.r=U+I.R$
$\Rightarrow {{U}_{AB}}=U=I{{R}_{N}}=\xi -I.r$ là độ giảm thế mạch ngoài (hay hiệu điện thế mạch ngoài).
- Hiện tượng đoản mạch là hiện tượng khi điện trở ngoài ${{R}_{N}}=0$ hay nối hai cực của một nguồn điện chỉ bằng dây dẫn có điện trở rất nhỏ thì cường độ dòng điện lớn nhất: $I=\frac{\xi }{r}$
- Hiệu suất của nguồn điện: $H=\frac{{{P}_{ich}}}{{{P}_{nguon}}}=\frac{U}{\xi }=\frac{I.{{R}_{N}}}{I.{{R}_{N}}+I.r}=\frac{{{R}_{N}}}{{{R}_{N}}+r}$
BÀI TẬP LUYỆN TẬP DẠNG 1
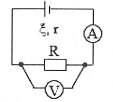
| Bài tập 1: Cho mạch điện như hình vẽ, với ampe-kế có điện trở không đáng kể, còn vôn-kế có điện trở vô cùng lớn. Biết nguồn điện có $\xi =9 V$; $r=0,5 A$ và điện trở $R=4 \Omega $. Số chỉ của vôn kế và ampe kế lần lượt bằng bao nhiêu?
|
Lời giải chi tiết
Ampe kế chỉ cường độ dòng điện chạy trong mạch chính: $I=\frac{\xi }{R+r}=\frac{9}{4+0,5}=2 A$
Vôn kế chỉ hiệu điện thế hai đầu điện trở chính là hiệu điện thế hai đầu mạch ngoài:
$U=\xi -I.r=9-2.0,5=8 V$.
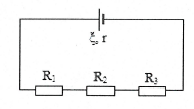
| Bài tập 2: Cho mạch điện như hình. Biết nguồn điện có suất điện động $\xi =12 V$ và có điện trở trong $r=1 \Omega $, các điện trở ${{R}_{1}}=10 \Omega $, ${{R}_{2}}=5 \Omega $ và ${{R}_{3}}=8 \Omega $.
a) Tính tổng trở ${{R}_{N}}$ của mạch ngoài. b) Tính cường độ dòng điện I chạy qua nguồn điện và hiệu điện thế mạch ngoài U. c) Tính hiệu điện thế ${{U}_{1}}$ giữa hai đầu điện trở ${{R}_{1}}$. d) Tính hiệu suất H của nguồn điện. e) Tính nhiệt lượng tỏa ra ở mạch ngoài trong thời gian 10 phút.
|
Lời giải chi tiết
a) Tổng trở mạch ngoài: ${{R}_{N}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}=23 \Omega $
b) Cường độ dòng điện chạy qua nguồn: $I=\frac{\xi }{{{R}_{N}}+r}=\frac{12}{23+1}=0,5 A$
Hiệu điện thế mạch ngoài U: $U=I.{{R}_{N}}=0,5.23=11,5 V$
c) Hiệu điện thế giữa hai đầu điện trở ${{R}_{1}}$: ${{U}_{1}}=I.{{R}_{1}}=0,5.10=5 V$
d) Hiệu suất của nguồn điện: $H=\frac{U}{\xi }.100%=\frac{11,5}{12}.100%=95,83%$
e) Nhiệt lượng tỏa ra trong 10 phút ở mạch ngoài:
$Q={{I}^{2}}{{R}_{N}}t=0,{{5}^{2}}.23.(10.60)=3450 J=3,45 kJ$.
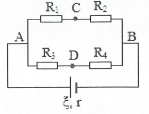
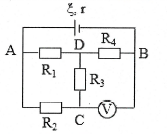
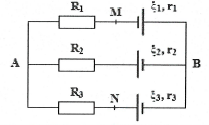
| Bài tập 3: Cho mạch điện như hình: $\xi =12 V$,$r=1 \Omega $, ${{R}_{1}}={{R}_{2}}=4 \Omega $, ${{R}_{3}}=3 \Omega $, ${{R}_{4}}=5 \Omega $.
a) Tìm điện trở tương đương mạch ngoài. b) Tìm cường độ dòng điện mạch chính và ${{U}_{AB}}$. Tìm cường độ dòng điện trong mỗi nhánh và ${{U}_{CD}}$.
|
Lời giải chi tiết
a) Ta có: $\left\{ \begin{array}{} {{R}_{12}}={{R}_{1}}+{{R}_{2}}=8 \Omega \\ {} {{R}_{34}}={{R}_{3}}+{{R}_{4}}=8 \Omega \\ \end{array} \right.$
Điện trở tương đương của mạch ngoài: ${{R}_{ng}}=\frac{{{R}_{12}}{{R}_{34}}}{{{R}_{12}}+{{R}_{34}}}=4 \Omega $
b) Cường độ dòng điện trong mạch chính: $I=\frac{\xi }{{{R}_{N}}+r}=2,4 A$
Hiệu điện thế giữa hai điểm A, B: ${{U}_{AB}}=I.{{R}_{N}}=9,6 V$
c) Do ${{R}_{12}}$ và ${{R}_{34}}$ bằng nhau, mà chúng mắc song song nên: ${{I}_{12}}={{I}_{34}}=\frac{{{U}_{AB}}}{{{R}_{12}}}=1,2 A$.
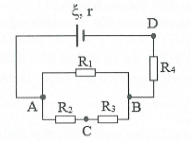
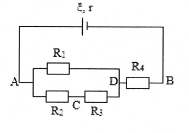
| Bài tập 4: Cho mạch điện như hình vẽ. Nguồn điện có suất điện động $\xi =9 V$ và điện trở trong $r=1 \Omega $. Các điện trở mạch ngoài ${{R}_{1}}={{R}_{2}}={{R}_{3}}=3 \Omega $, ${{R}_{4}}=6 \Omega $
a) Tính cường độ dòng điện chạy qua các điện trở và hiệu điện thế hai đầu mỗi điện trở. b) Tính hiệu điện thế giữa hai điểm C và D. c) Tính hiệu điện thế hai đầu nguồn điện và hiệu suất của nguồn điện.
|
Lời giải chi tiết
a) ${{R}_{23}}={{R}_{2}}+{{R}_{3}}=6 \Omega \Rightarrow {{R}_{AB}}=\frac{{{R}_{1}}.{{R}_{23}}}{{{R}_{1}}+{{R}_{23}}}=2 \Omega \Rightarrow {{R}_{N}}={{R}_{AB}}+{{R}_{4}}=8 \Omega $
Cường độ dòng điện trong mạch chính: $I=\frac{\xi }{{{R}_{N}}+r}=1 A\Rightarrow {{I}_{4}}=1 A$
Hiệu điện thế giữa hai đầu ${{R}_{4}}$: ${{U}_{4}}={{I}_{4}}{{R}_{4}}=6 V$
Hiệu điện thế giữa hai điểm A, B: ${{U}_{AB}}=I.{{R}_{AB}}=2 V\Rightarrow {{U}_{1}}={{U}_{23}}=2 V$
Dòng điện qua ${{R}_{1}}$: ${{I}_{1}}=\frac{{{U}_{1}}}{{{R}_{1}}}=\frac{2}{3} A$
Dòng điện qua ${{R}_{2}}$ và ${{R}_{3}}$ là: ${{I}_{23}}={{I}_{2}}={{I}_{3}}=I-{{I}_{1}}=1-\frac{2}{3}=\frac{1}{3} A$
Hiệu điện thế giữa hai đầu mỗi điện trở ${{R}_{2}}$ và ${{R}_{3}}$ là: $\left\{ \begin{array}{} {{U}_{2}}={{I}_{2}}{{R}_{2}}=1 V \\ {} {{U}_{3}}={{I}_{3}}{{R}_{3}}=1 V \\ \end{array} \right.$
b) Hiệu điện thế giữa hai điểm C và D: ${{U}_{CD}}={{U}_{3}}+{{U}_{4}}=1+6=7 V$
c) Hiệu điện thế hai đầu nguồn: $U=\xi -Ir=9-1=8 V$
Hiệu suất của nguồn: $H=\frac{U}{\xi }=\frac{8}{9}=88,89%$.
| Bài tập 5: Hai điện trở ${{R}_{1}}=2 \Omega $, ${{R}_{2}}=6 \Omega $ mắc vào nguồn $\left( \xi , r \right)$. Khi ${{R}_{1}}$, ${{R}_{2}}$ nối tiếp, cường độ trong mạch ${{I}_{N}}=0,5 A$. Khi ${{R}_{1}}$, ${{R}_{2}}$ song song, cường độ mạch chính ${{I}_{S}}=1,8 A$. Tìm $\xi , r$ |
Lời giải chi tiết
Khi $\left[ {{R}_{1}} nt {{R}_{2}} \right]\Rightarrow {{R}_{N}}={{R}_{1}}+{{R}_{2}}=2+6=8 \Omega $
$\Rightarrow {{I}_{N}}=\frac{\xi }{{{R}_{N}}+r}\Leftrightarrow 0,5=\frac{\xi }{8+r}$ (1)
Khi $\left[ {{R}_{1}}// {{R}_{2}} \right]\Rightarrow {{R}_{N}}=\frac{{{R}_{1}} {{R}_{2}}}{{{R}_{1}}+ {{R}_{2}}}=\frac{2.6}{2+6}=1,5 \Omega $
$\Rightarrow {{I}_{S}}=\frac{\xi }{{{R}_{N}}+r}\Leftrightarrow 1,8=\frac{\xi }{1,5+r}$ (2)
Từ (1) và (2), suy ra: $\left\{ \begin{array}{} 4+0,5r=\xi \\ {} 2,7+1,8r=\xi \\ \end{array} \right.\Rightarrow r=1 \Omega ; \xi =4,5 V$
| Bài tập 6: Acquy có $r=0,08 \Omega $. Khi dòng điện qua acquy là 4 A, nó cung cấp cho mạch ngoài một công suất bằng 8 W. Hỏi khi dòng điện qua acquy là 6 A, nó cung cấp cho mạch ngoài công suất bao nhiêu? |
Lời giải chi tiết
Hiệu điện thế mạch ngoài: $U=\xi -rI$.
Công suất cung cấp cho mạch ngoài: $P=UI=\left( \xi -rI \right)I$.
Với $I=4 A\Rightarrow P=\left( \xi -0,08.4 \right).4=8\Rightarrow \xi =2,32 V$.
Với ${I}'=6 A\Rightarrow {P}'=\left( 2,32=0,08.6 \right).6=11,04 W$.
Vậy khi dòng điện qua acquy là 6A, nó cung cấp cho mạch ngoài công suất là ${P}'=11,04 W$.
| Bài tập 7: Cho mạch điện như hình vẽ:$\xi =4,8 V$, $r=1 \Omega $, ${{R}_{1}}={{R}_{2}}={{R}_{3}}=3 \Omega $, ${{R}_{4}}=1 \Omega $, ${{R}_{V}}$ rất lớn.
a) Tìm số chỉ của vôn kế. b) Thay vôn kế bằng ampe kế có RA = 0. Tìm số chỉ của ampe kế. |
Lời giải chi tiết
a) Vì ${{R}_{V}}$ rất lớn nên bỏ đoạn CB đi mạch được vẽ lại như hình bên.
Tổng trở của mạch: ${{R}_{N}}={{R}_{4}}+\frac{{{R}_{1}}\left( {{R}_{2}}+{{R}_{3}} \right)}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}}=1+\frac{3.(3+3)}{3+3+3}=3 \Omega $
Cường độ dòng điện qua mạch chính: $I=\frac{\xi }{{{R}_{N}}+r}=\frac{4,8}{3+1}=1,2 A$
$\Rightarrow {{U}_{4}}={{I}_{4}}{{R}_{4}}=1,2.1=1,2 V$
${{U}_{3}}={{I}_{3}}{{R}_{3}}=\frac{{{U}_{AD}}}{{{R}_{23}}}.{{R}_{3}}=\frac{I{{R}_{AD}}}{{{R}_{23}}}.{{R}_{3}}$
Với ${{R}_{23}}={{R}_{2}}+{{R}_{3}}=3+3=6 \Omega $
$\Rightarrow {{R}_{AD}}\frac{{{R}_{1}}{{R}_{23}}}{{{R}_{1}}+{{R}_{23}}}=\frac{3.6}{3+6}=2 \Omega \Rightarrow {{U}_{3}}=\frac{1,2.2}{6}.3=1,2 V$
Vậy số chỉ của vôn kế là ${{U}_{CB}}={{U}_{CD}}+{{U}_{DB}}={{U}_{3}}+{{U}_{4}}=1,2+1,2=2,4 V$
b) Khi thay vôn kế bằng ampe kế có ${{R}_{A}}=0$ nên chập C với B, mạch được vẽ lại như hình bên. Xét tại nút C, số chỉ của ampe kế bằng: ${{I}_{A}}={{I}_{2}}+{{I}_{3}}$
Ta có: ${{R}_{134}}={{R}_{1}}+\frac{{{R}_{3}}{{R}_{4}}}{{{R}_{3}}+{{R}_{4}}}=3+\frac{3.1}{3+1}=3,75 \Omega $
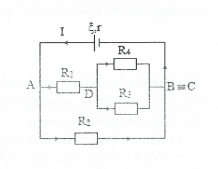
Điện trở mạch ngoài: ${{R}_{N}}=\frac{{{R}_{134}}.{{R}_{2}}}{{{R}_{134}}+{{R}_{2}}}=\frac{3,75.3}{3,75+3}=\frac{5}{3} \Omega $
Cường độ dòng điện qua mạch chính:
$I=\frac{\xi }{{{R}_{N}}+r}=\frac{4,8}{\frac{5}{3}+1}=1,8 A$ Và ${{I}_{2}}=\frac{{{U}_{AB}}}{{{R}_{2}}}=\frac{I.{{R}_{N}}}{{{R}_{2}}}=\frac{1,8.\frac{5}{3}}{3}=1 A$
${{I}_{1}}=I-{{I}_{2}}=1,8-1=0,8 A$
${{I}_{3}}=\frac{{{U}_{DB}}}{{{R}_{3}}}=\frac{{{I}_{1}}.{{R}_{DB}}}{{{R}_{3}}}=\frac{{{I}_{1}}.{{R}_{3}}.{{R}_{4}}}{{{R}_{3}}\left( {{R}_{3}}+{{R}_{4}} \right)}=\frac{{{I}_{1}}{{R}_{4}}}{{{R}_{3}}+{{R}_{4}}}=\frac{0,8.1}{3+1}=0,2 A$
Số chỉ của ampe kế: ${{I}_{A}}={{I}_{2}}+{{I}_{3}}=1+0,2=1,2 A$
DẠNG 2: ĐỊNH LUẬT ÔM CHO MẠCH CHỨA NGUỒN VÀ MÁY THU (Tham khảo)
PHƯƠNG PHÁP GIẢI

- Định luật Ohm chứa nguồn (máy phát):
Ta có: ${{U}_{AB}}={{U}_{AM}}+{{U}_{MB}}=-{{\xi }_{p}}+I.{{r}_{p}}+I.R\Rightarrow $
Đối với nguồn điện (máy phát): dòng điện đi vào cực âm và đi ra từ cực dương.
${{U}_{AB}}$: tính theo chiều dòng điện đi từ A đến B qua mạch $\left( {{U}_{AB}}=-{{U}_{BA}} \right)$
- Định luật Ohm cho đoạn mạch chứa máy thu điện:
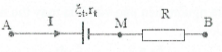
Ta có: ${{U}_{AB}}={{U}_{AM}}+{{U}_{MB}}={{\xi }_{t}}+I.{{r}_{t}}+I.R\Rightarrow $
Đối với máy thu ${{E}_{t}}$: dòng điện đi vào cực dương và đi ra từ cực âm.
${{U}_{AB}}$: tính theo chiều dòng điện đi từ A đến B qua mạch.
- Định luật Ohm cho đoạn mạch chứa cả nguồn và máy thu:
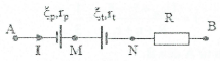
Ta có: ${{U}_{AB}}={{U}_{AM}}+{{U}_{MN}}+{{U}_{MB}}=-{{\xi }_{p}}+I.{{r}_{p}}+{{\xi }_{t}}+I.{{r}_{t}}+I.R\Rightarrow $
Phương pháp giải:
- ${{B}_{1}}$: Dòng I có chiều AB, nếu chưa có chiều I thì ta giả sử dòng I theo chiều $A\to B$ . Tại một điểm nút ta luôn có: $\sum{{{I}_{\tilde{n}e\acute{a}n}}=}\sum{{{I}_{\tilde{n}i}}}$ (nút là nơi giao nhau của ít nhất 3 nhánh).
- ${{B}_{2}}$: Dùng công thức định luật Ôm cho các đoạn mạch (công thức I) đề viết I qua các đoạn mạch
Hiệu điện thế giữa hai điểm A, B: $$
+) Lấy dấu “+” trước I khi dòng I có chiều AB
+) Lấy dấu “-” trước I khi dòng I ngược chiều AB
+) Khi đi từ A đến B gặp nguồn nào lấy nguồn đó, gặp cực nào trước lấy dấu cực đó.
Khi mạch kín thì ${{U}_{AB}}=0$, định luật Ohm cho đoạn mạch chứa cả nguồn và máy thu:
$$
- ${{B}_{3}}$: Thế các I ở bước 2 vào bước 1 $\Rightarrow {{U}_{AB}}$
- ${{B}_{4}}$: Thế ${{U}_{AB}}$ vào các phương trình ở bước 2 $\Rightarrow I$
- ${{B}_{5}}$: Nhận xét chiều của các I:
+) Nếu $I>0$ thì chiều dòng điện đã giả sử đúng
+) Nếu $I<0$ thì chiều dòng điện đã giả sử sai, chiều đúng là chiều ngược chiều đã giả sử.
BÀI TẬP LUYỆN TẬP DẠNG 2
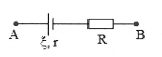 Bài tập 1: Cho đoạn mạch điện gồm một nguồn điện $\xi =12 V$, $r=0,5 \Omega $ nối tiếp với một điện trở $R=5,5 \Omega $. Hiệu điện thế hai đầu đoạn mạch AB là 6V. Cường độ dòng điện chạy qua mạch là I bằng bao nhiêu? Bài tập 1: Cho đoạn mạch điện gồm một nguồn điện $\xi =12 V$, $r=0,5 \Omega $ nối tiếp với một điện trở $R=5,5 \Omega $. Hiệu điện thế hai đầu đoạn mạch AB là 6V. Cường độ dòng điện chạy qua mạch là I bằng bao nhiêu?
|
Lời giải chi tiết
Giả sử chiều dòng điện đi từ A đến B.
Ta có: ${{U}_{AB}}=-\xi +I\left( r+R \right)\Rightarrow I=\frac{{{U}_{AB}}+\xi }{r+R}=\frac{-6+12}{0,5+5,5}=1 A$.
Vậy dòng điện có chiều từ A đến B và ${{I}_{AB}}=1 A$.
Lời giải chi tiết
a) Giả sử dòng điện trong đoạn mạch có chiều từ A đến B. Khi đó ${{\xi }_{1}}$ là máy phát, ${{\xi }_{2}}$ là máy thu. Áp dụng định luật ôm cho đoạn mạch AB, ta có:
${{U}_{AB}}=-{{\xi }_{1}}+I{{r}_{1}}+{{\xi }_{2}}+I{{r}_{2}}+IR\Rightarrow I=\frac{{{U}_{AB}}+{{\xi }_{1}}-{{\xi }_{2}}}{R+{{r}_{1}}+{{r}_{2}}}=\frac{1}{3} A$
Vì $I>0$ nên dòng điện có chiều từ A đến B.
b) ${{\xi }_{1}}$ là máy phát vì dòng điện đi ra từ cực dương. Còn ${{\xi }_{2}}$ là máy thu vì dòng điện đi vào từ cực dương.
c) Hiệu điện thế giữa hai điểm A và C: ${{U}_{AC}}=-{{\xi }_{1}}+I.{{r}_{1}}=-7,6 V$
Hiệu điện thế giữa hai điểm C và B: ${{U}_{CB}}={{\xi }_{2}}+I.\left( {{r}_{1}}+R \right)=13,6 V$.
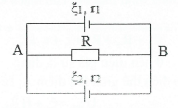
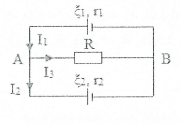
| Bài tập 3: Cho mạch điện như hình vẽ: ${{\xi }_{1}}=8 V$, ${{\xi }_{2}}=7 V$, ${{r}_{1}}=1 \Omega $, $R=1 \Omega $, ${{r}_{2}}=1 \Omega $.
a) Tìm ${{U}_{AB}}$. b) Cường độ dòng điện qua các nhánh. |
Lời giải chi tiết
Giả sử chiều dòng điện như hình vẽ.
Tại nút A: ${{I}_{1}}={{I}_{2}}+{{I}_{3}}$ (*)
${{I}_{1}}=\frac{{{U}_{BA}}+{{\xi }_{1}}}{{{r}_{1}}}=-{{U}_{AB}}+8$ (1)
${{I}_{2}}=\frac{{{U}_{AB}}-{{\xi }_{2}}}{{{r}_{2}}}={{U}_{AB}}-7$ (2)
${{I}_{3}}=\frac{{{U}_{AB}}}{R}={{U}_{AB}}$ (3)
Thế ${{I}_{1}}$, ${{I}_{2}}$, ${{I}_{3}}$ vào (*), suy ra: $-{{U}_{AB}}+8={{U}_{AB}}-7+{{U}_{AB}}\Rightarrow {{U}_{AB}}=5 V$
b) Thay ${{U}_{AB}}$ vào các phương trình trên ta được:
${{I}_{1}}=-{{U}_{AB}}+8=-5+8=3 A$; ${{I}_{2}}={{U}_{AB}}-7=5-7=2 A$; ${{I}_{3}}={{U}_{AB}}=5 A$
Do ${{I}_{1}}, {{I}_{3}}>0\Rightarrow $ Chiều dòng điện ${{I}_{1}}$, ${{I}_{3}}$ là đã giả sử đúng
${{I}_{2}}<0\Rightarrow $ Chiều dòng điện đã giả sử là sai. chiều ${{I}_{2}}$ đúng phải ngược chiều đã giả sử.
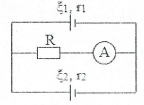
| Bài tập 4: Cho mạch điện như hình vẽ: ${{\xi }_{1}}=6 V$, ${{\xi }_{2}}=4,5 V$, ${{r}_{1}}=2 \Omega $, $R=2 \Omega $, ${{R}_{A}}=0$. Ampe kế chỉ 2A. Tính ${{r}_{2}}$.
|
Lời giải chi tiết
Giả sử dòng điện có chiều như hình vẽ, ta có:
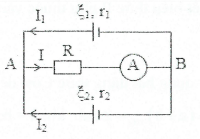
${{U}_{AB}}=IR=2.2=4 V$
Xét nhánh trên: ${{I}_{1}}=\frac{{{U}_{BA}}+{{\xi }_{1}}}{{{r}_{1}}}=\frac{-{{U}_{AB}}+{{\xi }_{1}}}{{{r}_{1}}}=\frac{6-4}{2}=1 A$ (1)
Xét nhánh dưới:
$-{{U}_{AB}}=-{{\xi }_{2}}+{{I}_{2}}.{{r}_{2}}\Leftrightarrow {{r}_{2}}=\frac{{{\xi }_{2}}-{{U}_{AB}}}{{{I}_{2}}}=\frac{4,5-4}{{{I}_{2}}}=\frac{0,5}{{{I}_{2}}}$ (2)
Tại nút A: $I={{I}_{1}}+{{I}_{2}}\Rightarrow {{I}_{2}}=I-{{I}_{1}}=2-1=1 A$
Thay vào (2) ta được: ${{r}_{2}}=0,5 \Omega $.
| Bài tập 5: Cho mạch điện như hình vẽ: ${{\xi }_{1}}=12 V$, ${{r}_{1}}=1 \Omega $, ${{\xi }_{2}}=6 V$, ${{r}_{2}}=2 \Omega $, ${{E}_{3}}=9 V$, ${{r}_{3}}=3 \Omega $, ${{R}_{1}}=4 \Omega $,${{R}_{2}}=2 \Omega $ , ${{R}_{3}}=3 \Omega $. Tính ${{U}_{AB}}$ và cường độ dòng điện qua mỗi điện trở.
|
Lời giải chi tiết
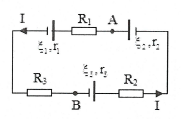
Giả sử chiều dòng điện trong mạch như hình
Áp dụng định luật ôm cho mạch kín, ta có:
$I=\frac{{{\xi }_{2}}+{{\xi }_{3}}-{{\xi }_{1}}}{{{R}_{1}}+{{R}_{2}}+{{R}_{3}}+{{r}_{1}}+{{r}_{2}}+{{r}_{3}}}=0,2 A$
Vì $I>0$ nên điều giả sử là đúng
Hiệu điện thế giữa hai điểm A, B:
${{U}_{AB}}={{\xi }_{1}}+I\left( {{R}_{1}}+{{R}_{3}}+{{r}_{1}} \right)=13,6 V$.
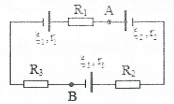
| Bài tập 6: Cho mạch điện như hình vẽ, trong đó ${{\xi }_{1}}=3 V$, ${{r}_{1}}=0,5 \Omega $, ${{\xi }_{2}}=6 V$, ${{r}_{2}}=1 \Omega $, ${{\xi }_{3}}=9 V$, ${{r}_{3}}=2\Omega $, ${{R}_{1}}=2,5 \Omega $, ${{R}_{2}}=3 \Omega $, ${{R}_{3}}=4 \Omega $. Tìm ${{U}_{MN}}$.
|
Lời giải chi tiết
Chọn chiều dòng điện như hình.
Xét vòng mạch có: $\left\{ \begin{array}{} -{{\xi }_{2}}-{{\xi }_{1}}={{I}_{2}}\left( {{R}_{2}}+{{r}_{2}} \right)+{{I}_{1}}\left( {{R}_{1}}+{{r}_{1}} \right) \\ {} {{\xi }_{2}}-{{\xi }_{3}}={{I}_{3}}\left( {{R}_{3}}+{{r}_{3}} \right)-{{I}_{2}}\left( {{R}_{2}}+{{r}_{2}} \right) \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} -9=4{{I}_{2}}+3{{I}_{3}} \\ {} -3=6{{I}_{3}}-4{{I}_{2}} \\ \end{array} \right.$ (1)
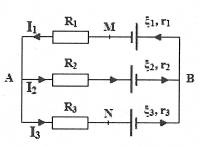
Tại nút A: ${{I}_{1}}-{{I}_{2}}-{{I}_{3}}=0$ (2)
Từ (1) và (2)$\Rightarrow {{I}_{1}}=\frac{-17}{9} A$; ${{I}_{2}}=\frac{-5}{6} A$; ${{I}_{3}}=\frac{-19}{18} A$
Ta có: ${{U}_{MA}}=\frac{-17}{9}.2,5=\frac{-85}{18} V$; ${{U}_{AN}}=\frac{-19}{18}.4=\frac{-38}{9} V$
$\Rightarrow {{U}_{MN}}={{U}_{MA}}+{{U}_{AN}}=\frac{-85}{18}+\frac{-38}{9}=-8,9 V$.
DẠNG 3: CÔNG SUẤT. CÔNG SUẤT CỰC ĐẠI.
PHƯƠNG PHÁP GIẢI
- Tìm R để công suất là hằng số: $P={{I}^{2}}R$
- Tìm R đề công suất cực đại:
Viết biểu thức P phụ thuộc vào R, biến đổi sao cho:
$P=\frac{\text{ha }\!\!\grave{\mathrm{e}}\!\!\text{ ng} \text{so }\!\!\acute{\mathrm{a}}\!\!\text{ }}{ch\ddot{o}\grave{u}a R}$
Sử dụng bất đẳng thức Côsi để đánh giá: $\left( a+b \right)\ge 2\sqrt{ab}$
$\Rightarrow {{\left( a+b \right)}_{\min }}=2\sqrt{ab}$ khi $a=b$.
BÀI TẬP LUYỆN TẬP DẠNG 3
| Bài tập 1: Điện trở $R=8 \Omega $ mắc vào 2 cực một acquy có điện trở trong $r=1 \Omega $. Sau đó người ta mắc thêm điện trở R nối tiếp với điện trở cũ. Hỏi công suất mạch ngoài tăng hay giảm bao nhiêu lần? |
Lời giải chi tiết
Cường độ dòng điện ban đầu trong mạch: ${{I}_{1}}=\frac{\xi }{R+r}$
Công suất mạch ngoài: ${{P}_{1}}=I_{1}^{2}R=\frac{R{{\xi }^{2}}}{{{\left( R+r \right)}^{2}}}$
Cường độ dòng điện sau khi mắc thêm R: ${{I}_{2}}=\frac{\xi }{2R+r}$
Công suất mạch ngoài: ${{P}_{2}}=\left( 2R \right)I_{2}^{2}=2R\frac{{{\xi }^{2}}}{{{\left( 2R+r \right)}^{2}}}$
$\Rightarrow \frac{{{P}_{2}}}{{{P}_{1}}}=\frac{2R{{\xi }^{2}}}{{{\left( 2R+r \right)}^{2}}}.\frac{{{\left( R+r \right)}^{2}}}{R{{\xi }^{2}}}=\frac{2{{\left( R+r \right)}^{2}}}{{{\left( 2R+r \right)}^{2}}}=\frac{2{{\left( 8+1 \right)}^{2}}}{{{\left( 2.8+1 \right)}^{2}}}=0,56$: công suất mạch ngoài giảm.
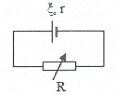
| Bài tập 2: Cho sơ đồ mạch điện như hình vẽ $\xi =12 V$, $r=2 \Omega $.
Cho $R=10 \Omega $. Tính công suất tỏa nhiệt trên R, công suất của nguồn; hiệu suất của nguồn.
a) Tìm R để công suất trên R là lớn nhất? Tính công suất đó ? b) Tính R để công suất tỏa nhiệt trên R là 16 W. |
Lời giải chi tiết
a) Ta có: $I=\frac{\xi }{R+r}=1 A$
Công suất tỏa nhiệt trên R: ${{P}_{R}}={{I}^{2}}R={{\left( \frac{\xi }{R+r} \right)}^{2}}R=10 W$
Công suất của nguồn: ${{P}_{nguon}}=\xi .I=12 W$
Hiệu suất của nguồn: $H=\frac{U}{\xi }=\frac{R}{R+r}=83,33%$.
b) Ta có: $I=\frac{\xi }{R+r}\Rightarrow P={{I}^{2}}R={{\left( \frac{\xi }{R+r} \right)}^{2}}R={{\left( \frac{\xi }{\sqrt{R}+\frac{r}{\sqrt{R}}} \right)}^{2}}$
Theo cô-si ta có: $\left( \sqrt{R}+\frac{r}{\sqrt{R}} \right)\ge 2\sqrt{r}\Rightarrow {{\left( \sqrt{R}+\frac{r}{\sqrt{R}} \right)}_{\min }}=2\sqrt{r}$
${{P}_{R\max }}=\frac{{{\xi }^{2}}}{4r}=18 W\Rightarrow R=r= 2 \Omega $.
d) Ta có: $I=\frac{\xi }{R+r}\Rightarrow P={{I}^{2}}R={{\left( \frac{\xi }{R+r} \right)}^{2}}R\Leftrightarrow 16={{\left( \frac{12}{R+r} \right)}^{2}}R\Rightarrow \left\{ \begin{array}{} R=4 \Omega \\ {} R=1 \Omega \\ \end{array} \right.$.
VẬT LÝ LỚP 12