Mặt trụ tròn xoay là gì? Lý thuyết và tính chất

Mặt trụ tròn xoay là gì? Lý thuyết và tính chất

1. Định nghĩa mặt tròn xoay

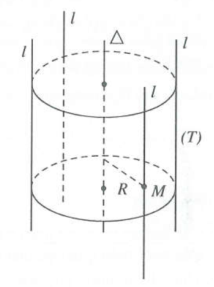
Cho hai đường thẳng l và Δ sao cho l song song Δ; $d\left( l;\Delta  \right)=R.$

Khi ta quay l quanh trục Δ một góc 360⁰ thì l tạo thành một mặt trụ tròn xoay (T) (mặt trụ).

• Δ gọi là trục của mặt trụ (T).

• l gọi là đường sinh của mặt trụ (T).

• R gọi là bán kính của mặt trụ (T).

2. Tính chất

a. Mặt trụ (T) là tập hợp các điểm M cách đường thẳng cố định Δ một khoảng R không đổi.

b. Nếu M₁ là một điểm bất kì trên mặt trụ thì đường thẳng l₁ đi qua M₁ và song song với Δ cũng nằm trên mặt trục đó

c. Nếu một mặt phẳng (P) vuông góc với trục Δ của mặt trụ (T) thì (P) cắt (T) theo giao tuyến đường tròn tâm I, bán kính R (I là giao điểm của Δ với (P))

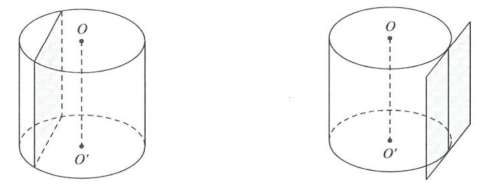
d. Cho một mặt phẳng (P) song song với trục Δ của một mặt trụ (T).

Khi đó

• (P) cắt (T) theo hai đường sinh $\Leftrightarrow d\left( \left( P \right);\Delta  \right)<R.$

• (P) tiếp xúc với (T) $\Leftrightarrow d\left( \left( P \right);\Delta  \right)=R.$

• $\left( P \right)\cap \left( T \right)=\varnothing \Leftrightarrow d\left( \left( P \right);\Delta  \right)>R.$