Mặt nón Hình nón Khối nón là gì? Định nghĩa

Mặt nón Hình nón Khối nón là gì? Định nghĩa

Định nghĩa mặt nón

Cho đường thẳng ∆. Xét một đường thẳng d cắt ∆ tại S tạo thành một góc α với $0<\alpha <\frac{\pi }{2}$. Mặt tròn xoay sinh bởi đường thẳng d như thế khi quay quanh ∆ gọi là mặt nón tròn xoay (hay đơn giản hơn là mặt nón)

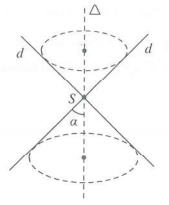
l ∆ gọi là trục của mặt nón

l D gọi là đường sinh của mặt nón

l S gọi là đỉnh của mặt nón

l Góc 2α gọi là góc ở đỉnh của mặt nón (hình vẽ bên)

Hình nón và khối nón

Cho mặt nón (N) với trục ∆ , đỉnh S, góc ở đỉnh 2α

Gọi (P) là mặt phẳng vuông góc với A tại điểm I khác S. Mặt phẳng (P) cắt mặt nón theo một đường tròn (C) có tâm I. Lại gọi (P’) là mặt phẳng vuông góc với A tại S.

Khi đó: Phần của mặt nón (N) giới hạn bởi hai mặt phẳng (P) và (P’) cùng với hình tròn xác định bởi (C) được gọi là hình nón:

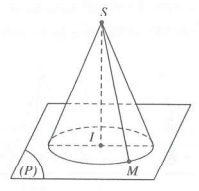
l S gọi là đỉnh của hình nón

l Đường tròn (C) gọi là đường tròn đáy của hình nón

l Với mỗi điểm M nằm trên đường tròn (C), đoạn thẳng SM gọi là đường sinh của hình nón

l Đoạn thẳng SI gọi là trục của hình nón (đó chính là khoảng cách từ đỉnh S đến mặt đáy)

l Một hình nón chia không gian thành hai phần: phần bên trong và phần bên ngoài của nó. Hình nón cùng với phần bên trong của nó gọi là khối nón