Mạch dao động LC là gì? Lý thuyết tóm tắt ngắn gọn

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1. Khái niệm mạch dao động LC

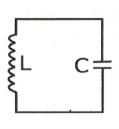
+) Mạch dao động là một mạch điện kín gồm một tụ điện có điện dung C và một cuộn dây có độ tự cảm L, có điện trở thuần không đáng kể nối với nhau.

+) Khi $r=0$ ta có mạch dao động lý tưởng.

+) Khi $r>0$ ta có mạch dao động tắt dần.

2. Hoạt động của mạch LC

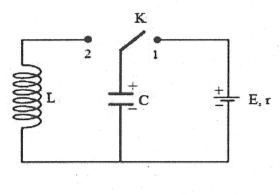
Ban đầu: Khoá K ở vị trí (1) tụ được nạp điện đến điện tích cực đại ${{Q}_{0}}$

Chuyển khoá K từ (1) sang (2) khi đó tụ bắt đầu phóng điện và qua cuộn cảm có dòng điện tự cảm.

Khi $q=0\Rightarrow $ dòng điện nạp ngược trở lại cho tụ điện quá trình đó cứ tiếp diễn tạo ra mạch dao động điện từ LC.

3. Khảo sát dao động điện từ tự do trong mạch dao động

+) Khi khoá K chuyền từ (1) sang (2) khi đó qua L xuất hiện suất điện động tự cảm: $e=-L\frac{di}{dt}$.

Khi $r=0\Rightarrow u=e=-Li$ mà $q=Cu\Rightarrow u=\frac{q}{C}\Rightarrow \frac{q}{C}+L{i}'=0$.

Lại có: $i=\frac{dq}{dt}={q}'(t)\Rightarrow {i}'={q}''(t)\Rightarrow \frac{q}{C}+L.{q}''=0\Rightarrow {q}''+\frac{1}{LC}q=0$.

Đặt $\frac{1}{LC}={{\omega }^{2}}\Rightarrow {q}''+{{\omega }^{2}}q=0$

Phương trình có nghiệm là: $q={{Q}_{0}}\cos (\omega t+\varphi )$.

Vậy trong mạch dao động LC thì điện tích dao động điều hòa với phương trình: $q={{Q}_{0}}\cos (\omega t+\varphi )$.

Trong đó tần số góc riêng $\omega =\frac{1}{\sqrt{LC}}$.

Khi đó:

1. Dòng điện: $i={q}'(t)=-\omega {{Q}_{0}}\sin (\omega t+\varphi )=\omega {{Q}_{0}}\cos \left( \omega t+\varphi +\frac{\pi }{2} \right)$.

Suy ra i sớm pha hơn q góc $\frac{\pi }{2}$ và ${{I}_{0}}=\omega {{Q}_{0}}$.

2. Do $q=Cu\Rightarrow u=\frac{{{Q}_{0}}}{C}\cos (\omega t+\varphi )={{U}_{0}}\cos (\omega t+\varphi )$.

Kết luận: Nếu $$ (Đơn vị Cu-lông C) thì $$ và $$ trong đó $$.

4. Phương pháp giải

Tần số góc riêng $\omega =\frac{1}{\sqrt{LC}}$, chu kì dao động riêng $T=2\pi \sqrt{LC}$, tần số riêng $f=\frac{1}{2\pi \sqrt{LC}}$.

Do $q\bot i$ nên ta có ${{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{q}{{{Q}_{0}}} \right)}^{2}}=1, i\bot u\Rightarrow {{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}+{{\left( \frac{u}{{{U}_{0}}} \right)}^{2}}=1$.