Khúc xạ ánh sáng phản xạ toàn phần là gì?

LÝ THUYẾT TRỌNG TÂM

1. Phản xạ, khúc xạ ánh sáng

Tia sáng SI khi đi từ môi trường trong suốt này sang môi trường trong suốt khác, tại điểm tới I bị tách thành hai phần, rnột phần phản xạ trở lại môi trường tới, một phần khúc xạ sang môi trường thứ hai.

Ðịnh luật phản xạ ánh sáng:

Tia khúc xạ nằm trong mặt phẳng chứa tia tới và đường pháp tuyến của mặt phân cách giữa hai môi trường. Góc tới bằng góc phản xạ: i = i'.

Ðịnh luật khúc xạ ánh sáng:

Tia khúc xạ nằm trong mặt phẳng tới, ở phía bên kia pháp tuyến so với tia tới. Tỉ số giữa sin góc tới i và sin góc khúc xạ r luôn luôn không đổi:

$\frac{\sin i}{\sin r}={{n}_{21}}=\frac{{{n}_{2}}}{{{n}_{1}}}\Rightarrow \left\{ \begin{matrix}{{n}_{1}}<{{n}_{2}}\Rightarrow r<i  \\{{n}_{1}}>{{n}_{2}}\Rightarrow r>i  \\\end{matrix} \right.$

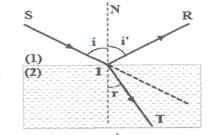
${{n}_{1}}<{{n}_{2}}\Rightarrow r<i$    ${{n}_{1}}>{{n}_{2}}\Rightarrow r>i$

Chú ý:

+) Nếu i = 0 thì r = 0: tia sáng truyền vuông góc với mặt phân cách thì truyền thẳng.

+) Nếu tia phản xạ vuông góc với tia khúc xạ $\text{(i + r = 9}{{\text{0}}^{\text{o}}}\text{ ) }\Rightarrow \text{sin r = cos}\,\,\text{i }\Rightarrow \text{tan i =}\frac{{{\text{n}}_{\text{2}}}}{{{\text{n}}_{\text{1}}}}\text{ }$

Chiết suất của môi trường:

+) n₁, n₂ được gọi là chiết suất tuyệt đối của môi trường 1 và 2 đối với chân không. Chiết suất tuyệt đối cho biết vận tốc truyền ánh sáng trong môi trường đó nhỏ hơn vận tốc truyền ánh sáng trong chân không bao nhiêu lần: ${{n}_{1}}=\frac{c}{{{v}_{1}}};{{n}_{2}}=\frac{c}{v2}$ với c = 3.10⁸ m/s là vận tốc ánh sáng truyền trong chân không.

Do $v\le c\Rightarrow n$ luôn $\ge 1,\,\,\,{{n}_{kh\hat{o}ngkh\acute{i}}}\approx {{n}_{ch\hat{a}nkh\hat{o}ng}}=1$

+) n₂₁ là là chiết suất tỉ đối giữa hai môi trường: ${{n}_{21}}=\frac{{{n}_{2}}}{{{n}_{1}}}=\frac{{{v}_{1}}}{{{v}_{2}}}.$

2. Phản xạ toàn phần

-  

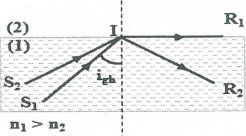
-  Phản xạ toàn phần là hiện tượng phản xạ toàn bộ ánh sáng tới, xảy ra ở mặt phân cách giữa hai môi trường trong suốt.

-  Ðiều kiện để có hiện tượng phản xạ toàn phần:

+) Tia sáng truyền từ môi trường có chiết suất lớn sang môi trường có chiết suất nhỏ hơn: n₂< n₁

+) Góc tới lớn hơn hoặc bằng góc giới hạn phản xạ toàn phần: $i\ge {{i}_{gh}}$

Với i_gh là góc tới giới hạn phản xạ toàn phần:

$\sin {{i}_{gh}}=\frac{{{n}_{2}}}{{{n}_{1}}}(r={{90}^{o}})$

3. Lăng kính

Khái niệm:

Lăng kính là một khối chất trong suốt hình lăng trụ có tiết diện là một tam giác. Đường đi của tia sáng qua lăng kính sau hai lần khúc xạ và không bị phản xạ toàn phần như sau:

Trong hình vẽ :

i_l là góc tới

r₁ là góc khúc xạ củaa tia sáng ở lần khúc xạ thứ nhất

r₂ là góc tới của tia sáng ở lần khúc xạ thứ hai

i₂ là góc ló, cũng là góc khúc xạ ở lần khúc xạ thứ hai

D là góc lệch của tia ló so vói tia tới (xét về phương diện hướng truyền)

A là góc chiết quang, là góc hợp bởi hai mặt bên. Tia sáng ló JR qua lăng kính bị lệch về phía đáy của lăng kính so với phương của tia sáng tới.

Các công thức của lăng kính :

$\left\{ \begin{matrix}\sin {{i}_{1}}=n.{{\sin }_{1}}  \\\sin {{i}_{2}}=n.{{\sin }_{2}}  \\A={{r}_{1}}+{{r}_{2}}  \\D={{i}_{1}}+{{i}_{2}}-A  \\\end{matrix} \right.$

Khi góc i_l và A < 10⁰  thì $\left\{ \begin{array}{} {{i}_{1}}=n\,{{r}_{1}}\, ;\,\,{{i}_{2}}=n\,{{r}_{2}} \\ {} A={{r}_{1}}+{{r}_{2}} \\ {} D=(n-1)A \\ \end{array} \right.$

Góc lệch cực tiểu :

Khi tia sáng có góc lệch cực tiểu thì đường đi của tia sáng đối xứng qua mặt phân giác của góc chiết quang của lăng kính :${{r}_{1}}={{r}_{2}}=\frac{A}{2} ;{{i}_{1}}={{i}_{2}}=i=\frac{{{D}_{\min }}+A}{2} ;{{D}_{\min }}=2i-A$

Góc lệch đạt cực tiểu ${{D}_{\min }} :\sin \frac{{{D}_{\min }}+A}{2}=n.\sin \frac{A}{2}$

Khi tăng dần góc tới i_l từ 0^o  lên thì góc lệch D giảm dần xuống giá trị cực tiểu  D_min  rồi lại tăng lên.

Điều kiện để có tia ló ra ở mặt bên thứ 2 :

$\left\{ \begin{array}{} A\le 2{{r}_{2gh}} \\ {} i\ge {{i}_{o}} \\ {} \sin {{i}_{o}}=n.\sin (A-{{r}_{2gh}}) \\ \end{array} \right.$