Hàm số mũ là gì? Lý thuyết và công thức tóm tắt ngắn gọn

Hàm số mũ là gì? Định nghĩa, tập xác định, đạo hàm và đồ thị

1. Định nghĩa hàm số mũ cơ số a là gì?

Cho số thực $\left\{ \begin{align}  & a>0 \\  & a\ne 1 \\ \end{align} \right..$ Hàm số $y={{a}^{x}}$ được gọi là hàm số mũ cơ số $a.$

2. Tập xác định của hàm số mũ

Tập xác định của hàm số $y={{a}^{x}}$ là : $D=\mathbb{R}$

Do $y={{a}^{x}}>0;\forall x\in \mathbb{R}$ suy ra tập giá trị của hàm số $y={{a}^{x}}$ là $T=\left( 0;+\infty  \right)$

3. Đạo hàm của hàm số mũ

Đạo hàm: ${{\left( {{a}^{u}} \right)}^{\prime }}={{a}^{u}}\ln a.u'\Rightarrow \left| \begin{align}  & {{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln a \\  & {{\left( {{e}^{x}} \right)}^{\prime }}={{e}^{x}} \\  & {{\left( {{e}^{u}} \right)}^{\prime }}={{e}^{u}}.u' \\ \end{align} \right..$ Công thức giới hạn: $\underset{t\to 0}{\mathop{\lim }}\,\frac{{{e}^{t}}-1}{t}=1.$

Với hàm số $y={{a}^{x}}$ ta có: $y'={{a}^{x}}\ln a$

• Với $a>1$ khi đó $y'={{a}^{x}}\ln a>0.$ Hàm số luôn đồng biến

Trong trường hợp $a>1$ ta có $\underset{x\to -\infty }{\mathop{\lim }}\,y=\underset{x\to -\infty }{\mathop{\lim }}\,{{a}^{x}}=0$ do đó đồ thị hàm số nhận trục hoành là tiệm cận ngang

• Với $0<a<1$ khi đó $y'={{a}^{x}}\ln a<0.$ Hàm số luôn nghịch biến

Trong trường hợp $a<1$ ta có $\underset{x\to +\infty }{\mathop{\lim }}\,y=\underset{x\to +\infty }{\mathop{\lim }}\,{{a}^{x}}=0$ do đó đồ thị hàm số nhận trục hoành là tiệm cân ngang

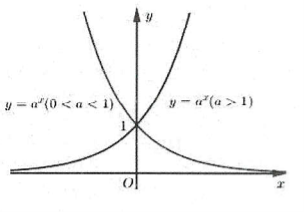
4. Đồ thị hàm số mũ $y={{a}^{x}}$

Đồ thị hàm số $y={{a}^{x}}$ nhận trục $Ox$ là tiệm cận ngang và luôn đi qua các điểm $\left( 0;1 \right)$ và $\left( 1;a \right)$

Đồ thị hàm số $y={{a}^{x}}$ nằm phía trên trục hoành $\left( y={{a}^{x}}>0\forall x\in \mathbb{R} \right)$