Hai mặt phẳng vuông góc với nhau khi nào ? Góc giữa hai mặt phẳng

Hai mặt phẳng vuông góc với nhau khi nào ? Góc giữa hai mặt phẳng

I. Góc giữa hai mặt phẳng

– Định nghĩa: 

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

– Cách xác định góc giữa hai mặt phẳng:

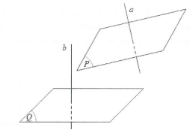
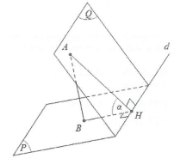
Tìm giao tuyến d của hai mặt phẳng (P) ; (Q).

Lấy A $\in $mp(Q), dựng $AB\bot mp(P)(B\in (P)).$

Vẽ BH vuông góc với d thì AH vuông góc d.

Vậy $\widehat{AHB}=\alpha $ (0 < α ≤ 90°) là góc giữa hai mặt phẳng (P) và (Q).

– Định lý : 

Gọi S là diện tích của đa giác H trong mặt phẳng (P) và S’ là diện tích hình chiếu H’ của H trên mặt phẳng (P’) thì S’ = S cosφ, trong đó φ là góc giữa hai mặt phẳng (P) và (P’).

II. Hai mặt phẳng vuông góc

– Định nghĩa: 

Hai mặt phẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng 90°.

– Định lý 1:

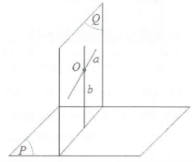
Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác thì hai mặt phẳng đó vuông góc với nhau.

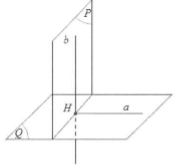
– Định lý 2:

Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau thì bất cứ đường thẳng a nào nằm trong (P), vuông góc với giao tuyến của (P) và (Q) đều vuông góc với mặt phẳng (Q).

- Hệ quả 1: 

Nếu hai mặt phẳng (P) và (Q) vuông góc với nhau và A là một điểm nẳm trong (P) thì đường thẳng a đi qua điểm A và vuông góc với (Q) sẽ nằm trong (P).

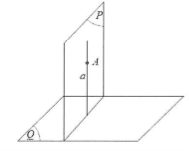
Hệ quả 1 được viết gọn là: $\left\{ \begin{array}  {} (P)\bot (Q) \\  {} A\in (P) \\  {} a\bot (Q) \\  {} A\in a \\ \end{array} \right.\Rightarrow a\subset (P)$

- Hệ quả 2: 

Nếu hai mặt phẳng cắt nhau và vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.

Hệ quả 2 được viết gọn là: $\left\{ \begin{array}  {} (P)\cap (Q)=a \\ {} (P)\bot (R) \\  {} (Q)\bot (R) \\ \end{array} \right.\Rightarrow a\bot (R)$

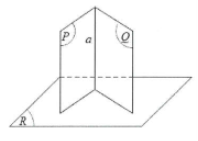
- Hệ quả 3: 

Qua đường thẳng a không vuông góc với mặt phẳng (P) có duy nhất mặt phẳng (Q) vuông góc với mặt  phẳng (P).

þ Hình lăng trụ đứng: Là hình lăng trụ có tất cả các cạnh bên vuông góc với mặt đáy.

þ Hình lăng trụ đều: Là hình lăng trụ đứng có đáy là đa giác đều.

þ Hình hộp đứng: Là hình lăng trụ đứng có đáy là hình bình hành.

þ Hình hộp chữ nhật: Là hình lăng trụ đứng có đáy là hình chữ nhật.

þ Hình lập phương: Là hình lăng trụ đứng có đáy là hình vuông và các mặt bên đều là hình vuông.

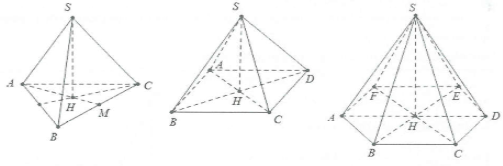
þ Hình chóp đều: Một hình chóp được gọi là hình chóp đều nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau.

Dưới đây là hình vẽ của hình chóp tam giác đều, tứ giác đều và hình chóp lục giác đều.