Giá trị lớn nhất (Max), giá trị nhỏ nhất (Min) của hàm số là gì?

Giá trị lớn nhất, giá trị nhỏ nhất – Lý thuyết phương pháp giải chung

1. Định nghĩa GTLN GTNN

Cho hàm số xác định trên D

•    Số M được gọi là giá trị lớn nhất (GTLN) của hàm số 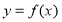  trên D nếu

$\left\{ \begin{array}  {} f(x)\le M;\forall x\in D \\  {} \exists {{x}_{o}}\in D:f({{x}_{o}})=M \\ \end{array} \right.,$ ta kí hiệu $M=\underset{x\in D}{\mathop{\max }}\,f(x)$

Chú ý: Nếu $f(x)\le M;\forall x\in D$ thì ta chưa thể suy ra $M=\underset{x\in D}{\mathop{\max }}\,f(x)$

•    Số m được gọi là giá trị nhỏ nhất (GTNN) của hàm số $y=f(x)$ trên D nếu

$\left\{ \begin{array}  {} f(x)\ge M;\forall x\in D \\  {} \exists {{x}_{o}}\in D:f({{x}_{o}})=M \\ \end{array} \right.,$ ta kí hiệu$M=\underset{x\in D}{\mathop{\min }}\,f(x)$

Chú ý: Nếu $f(x)\ge M;\forall x\in D$ thì ta chưa thể suy ra $M=\underset{x\in D}{\mathop{\min }}\,f(x)$

.2. Các phương pháp tìm GTLN, GTNN của hàm số

Phương pháp chung:

Để tìm GTLN, GTNN của hàm số $y=f(x)$ trên D, ta tính y’, tìm các điểm mà tại đó đạo hàm triệt tiêu hoặc không tồn tại và lập bảng biến thiên. Từ bảng biến thiên ta suy ta GTLN, GTNN của hàm số.

v  Chú ý:

•    Nếu hàm số $y=f(x)$ luôn tăng hoặc giảm trên [a;b].

Thì ta có $\underset{\text{ }\!\![\!\!\text{ }a;b\text{ }\!\!]\!\!\text{ }}{\mathop{\max }}\,f(x)=\left\{ f(a);f(b) \right\}$ và $\underset{\text{ }\!\![\!\!\text{ }a;b\text{ }\!\!]\!\!\text{ }}{\mathop{\min }}\,f(x)=\left\{ f(a);f(b) \right\}$

•    Nếu hàm số $y=f(x)$ liên tục trên [a;b] thì luôn có GTLN, GTNN trên đoạn đó và để tìm GTLN, GTNN ta làm như sau:

-       Tính y’ và tìm các điểm ${{x}_{1}},{{x}_{2}},...,{{x}_{n}}$ mà tại đó y’ triệt tiêu hoặc không tồn tại.

-       Tính các giá trị $f({{x}_{1}}),f({{x}_{2}}),f({{x}_{3}}),...,f({{x}_{n}}).$ Khi đó

+) $\underset{\text{ }\!\![\!\!\text{ }a;b\text{ }\!\!]\!\!\text{ }}{\mathop{\max }}\,f(x)=\left\{ f({{x}_{1}});f({{x}_{2}});....f({{x}_{n}});f(a);f(b) \right\}$

+) $\underset{\text{ }\!\![\!\!\text{ }a;b\text{ }\!\!]\!\!\text{ }}{\mathop{\min }}\,f(x)=\left\{ f({{x}_{1}});f({{x}_{2}});....f({{x}_{n}});f(a);f(b) \right\}$

•    Nếu hàm số $y=f(x)$ tuần hoàn trên chu kỳ T để tìm GTLN, GTNN của nó trên D ta chỉ cần tìm GTLN, GTNN trên một đoạn thuộc D có độ dài bằng T.
•    Cho hàm số $y=f(x)$ xác định trên D. Khi đặt ẩn phụ $t=u(x),$ ta tìm được $t\in E$ với $\forall x\in D$, ta có $y=g(t)$ thì Max, Min của hàm  f  trên D chính là Max, Min của hàm g trên E.
•    Khi bài toán yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất mà không nói trên tập nào thì ta hiểu là tìm GTLN, GTNN trên tập xác định của hàm số.
•    Ngoài phương pháp khảo sát để tìm Max, Min ta có thể dùng phương pháp miền giá trị hoặc bất đẳng thức để tìm Max, Min

Ta cần phân biệt hai khái niệm cơ bản

-       Giá trị lớn nhất của hàm số $y=f(x)$ trên D với cực đại của hàm số.

-       Giá trị nhỏ nhất của hàm số $y=f(x)$ trên D với cực tiểu của hàm số.

3. Tìm tập giá trị của hàm số

Phương pháp chung:

Việc tìm tập giá trị của hàm số chính là việc đi tìm giá trị nhỏ nhất, kí hiệu là m và giá trị lớn nhất, kí hiệu là M. Khi đó, tập giá trị của hàm số là $T=\text{ }\!\![\!\!\text{ }m;M\text{ }\!\!]\!\!\text{ }.$

4. Phương pháp tìm GTLN, GTNN của hàm số hai biến (bài toán cực trị)

• Các bài toán hai biến (yêu cầu: tìm GTLN, GTNN hoặc tìm tập giá trị).

•    Sử dụng phương pháp thế $y=h(x)$ từ giả thiết vào biểu thức P cần tìm cực trị, khi đó $P=f(x)$ với $x\in \text{ }\!\![\!\!\text{ }a;b\text{ }\!\!]\!\!\text{ }\to $ đưa về tìm GTLN, GTNN của bài toán một biến.
•    Sử dụng các bất đẳng thức cơ bản (có thể dùng để giải quyết các bài toán một biến)
•    Bất đẳng thức AM – GM cho hai số thực không âm

$a+b\ge 2\sqrt{ab}\Leftrightarrow 4ab\le {{(a+b)}^{2}}\Leftrightarrow {{(a-b)}^{2}}\ge 0$

•    Bất đẳng thức Bunhiacopxki cho các số thực a, b, c, d

${{\left( ax+by \right)}^{2}}\le \left( {{a}^{2}}+{{b}^{2}} \right)\left( {{x}^{2}}+{{y}^{2}} \right).$ Dấu “=” xảy ra khi $\frac{a}{x}=\frac{b}{y}$

• Một số bổ đề cơ bản dùng trong các bài toán hai biến

•    $xy\le \frac{{{\left( x+y \right)}^{2}}}{4}\le \frac{\left( {{x}^{2}}+{{y}^{2}} \right)}{2}$ và ${{x}^{2}}+xy+{{y}^{2}}\ge \frac{3}{4}{{(x+y)}^{2}}$
•    ${{x}^{3}}+{{y}^{3}}\ge \frac{\left( x+y \right)\left( {{x}^{2}}+{{y}^{2}} \right)}{2}\ge \frac{{{(x+y)}^{3}}}{4}\ge xy(x+y)$
•    Bất đẳng thức Cauchy – Schwarz dạng phân số $\frac{1}{x}+\frac{1}{y}\ge \frac{4}{x+y}$