Đường thẳng vuông góc với mặt phẳng khi nào? Bài tập và cách chứng minh

Đường thẳng vuông góc với mặt phẳng khi nào? Bài tập và cách chứng minh

Phương pháp chứng minh đường thẳng vuông góc với mặt phẳng

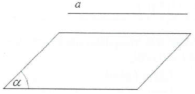
■ Định nghĩa: Một đường thẳng được gọi là song song với một mặt phẳng nếu chúng không có điểm chung.

Hình bên ta có: $a//\left( \alpha  \right).$

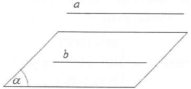
■ Định lý 1 : Nếu một đường thẳng a không nằm trong mặt phẳng $\left( \alpha  \right)$ và song song với một đường thẳng b nằm trên $\left( \alpha  \right)$ thì a song song với $\left( \alpha  \right)$.

■ Định lý 2: Cho đường thẳng a song song với mặt phẳng $\left( \alpha  \right)$. Khi đó nếu một mặt phẳng $\left( \beta  \right)$ chứa a và cắt $\left( \alpha  \right)$ theo giao tuyến b thì a song song với b.

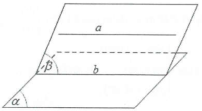
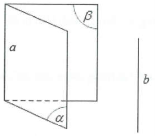
$\Rightarrow$Hệ quả: Nếu hai mặt phẳng $\left( \alpha  \right)$ và $\left( \beta  \right)$ cùng song song với một đường thẳng b thì giao tuyến (nếu có) của chúng cũng song song với b.

■ Định lý 3: Với hai đường thẳng a và b chéo nhau cho trước, có duy nhất một mặt phẳng $\left( \alpha  \right)$ chứa a và song song với b.

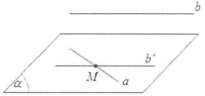
Với hai đường thẳng phân biệt a và b không song song với nhau, và một điểm O cho trước, có duy nhất một mặt phẳng $\left( \alpha  \right)$ qua O và song song với (hoặc chứa) a và b.

Phương pháp giải toán:

Để chứng minh đường thẳng d song song với mặt phẳng (P) ta sẽ chứng minh đường thẳng d không nằm trong (P) đồng thời song song với một đtrờng thẳng nằm trong mặt phẳng (P).

Bài tập trắc nghiệm chứng minh vuông góc giữa đường thẳng với mặt phẳng có đáp án chi tiết

Lời giải chi tiết

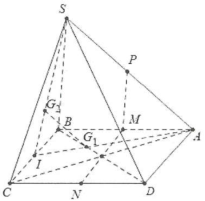
a) Vì M, N là trung điểm của AB, CD nên $MN//AD//BC$

Ta có: $\left\{ \begin{array}  {} AD\in \left( SAD \right) \\  {} MN//AD \\  {} \text{MN}\notin \left( SAD \right)\text{ } \\ \end{array} \right.\Rightarrow MN//\left( SAD \right).$

Tương tự ta có: $\left\{ \begin{array}  {} BC\in \left( SBC \right) \\  {} MN//BC \\  {} \text{MN}\notin \left( SBC \right)\text{ } \\ \end{array} \right.\Rightarrow MN//\left( SBC \right).$

b) Vì P là trung điểm của SA nên $\left\{ \begin{array}  {} MP//SB \\  {} NP//SC \\ \end{array} \right.$

Ta có: $\left\{ \begin{array}  {} MP\in \left( MNP \right) \\  {} SB//MP \\  {} \text{SB}\notin \left( MNP \right)\text{ } \\ \end{array} \right.\Rightarrow SB//\left( MNP \right).$

Tương tự chứng minh trên ta có: $\left\{ \begin{array}  {} NP\in \left( MNP \right) \\  {} SC//NP \\  {} \text{SC}\notin \left( MNP \right)\text{ } \\ \end{array} \right.\Rightarrow SC//\left( MNP \right).$

c) Gọi I là trung điểm của BC $\Rightarrow \left\{ \begin{array}  {} {{G}_{1}}\in AI \\  {} {{G}_{2}}\in BC \\ \end{array} \right.$ và $\frac{I{{G}_{1}}}{IA}=\frac{I{{G}_{2}}}{IS}=\frac{1}{3}\Rightarrow {{G}_{1}}{{G}_{2}}//SA\Rightarrow {{G}_{1}}{{G}_{2}}//\left( SAC \right).$

Lời giải chi tiết

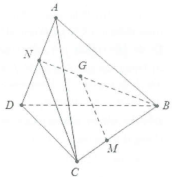
Gọi N là trung điểm của AD

Vì G là trọng tâm của tam giác ABC nên $BG=2GN$

Mà $MB=2MC$ nên $\frac{BG}{GN}=\frac{MB}{MB}\Rightarrow MG//NC.$

Ta có: $\left\{ \begin{array}  {} NC\in \left( ACD \right) \\  {} MG//NC \\  {} \text{MG}\notin \left( ACD \right)\text{ } \\ \end{array} \right.\Rightarrow MG//\left( ACD \right).$

Lời giải chi tiết

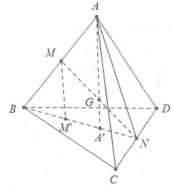
a)Trong mp(ABN): Gọi ${A}'=AG\cap BN$

$\Rightarrow {A}'=AG\cap \left( BCD \right).$

b) Xét trong mp(ABN): Kẻ $M{M}'//A{A}'$ cắt BN tại ${M}'\Rightarrow {M}'\in BN.$

Do M là trung điểm của AB nên $M{M}'$ là đường trung bình trong $\Delta AB{A}'\Rightarrow {M}'B={M}'A.$

Do G là trung điểm của MN mà $G{A}'//M{M}'$ nên $G{A}'$ là đường trung bình trong $\Delta MN{M}'$ suy ra ${A}'$ là trung điểm của ${M}'N$ hay ${M}'{A}'=N{A}'.$

Suy ra $B{M}'={M}'{A}'={A}'N.$

c) Ta có: $\left\{ \begin{array}  {} \frac{M{M}'}{{A}'A}=\frac{BM}{BA}=\frac{1}{2} \\  {} \frac{G{A}'}{M{M}'}=\frac{{A}'N}{{M}'N}=\frac{1}{2} \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} A{A}'=2M{M}' \\  {} M{M}'=2G{A}' \\ \end{array} \right.$

$\Rightarrow {A}'A=2M{M}'=4G{A}'\Leftrightarrow AG=3G{A}'.$

Lời giải chi tiết

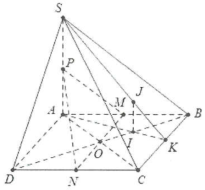
a) Ta có: ABCD là hình bình hành và M, N lần lượt là trung điểm của AB và CD nên $MN//AD//BC.$

Do đó $MN//\left( SBC \right)$ và $MN//\left( SAD \right).$

b) Trong tam giác SAB có M, P lần lượt là trung điểm của AB và SA nên MP là đường trung bình suy ra

$MP//SP\Rightarrow SP//\left( MNP \right).$

Dễ thấy AMCN là hình bình hành nên giao điểm O của chúng là trung điểm của AC và $MN\Rightarrow O\in \left( MNP \right).$

Trong mặt phẳng (SAC) có PO là đường trung bình của $\Delta SAC$ nên $PO//SC\Rightarrow SC//\left( MNP \right).$

c) Gọi K trung điểm của BC $\Rightarrow \left\{ \begin{array}  {} \frac{AI}{AK}=\frac{2}{3} \\  {} \frac{SJ}{SK}=\frac{2}{3} \\ \end{array} \right.$ (tính chất trọng tâm tam giác)

Do đó $\text{IJ}//SA\Rightarrow \text{IJ}//\left( SAB \right),\text{IJ}//\left( SAD \right)$ và $\text{IJ}//\left( SAC \right)$.

Lời giải chi tiết

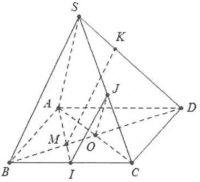
a) Do ABCD là hình bình hành nên O là trung điểm của AC và BD.

Ta có: OJ là đường trung bình trong tam giác SAC nên $OJ//SA$ suy ra $OJ//\left( SAC \right)$ và $OJ//\left( SAB \right)$.

b) OI là đường trung bình trong tam giác ABC nên $OI//AB\Rightarrow OI//CD\Rightarrow OI//\left( SCD \right).$

Tương tự IJ là đường trung bình trong tam giác SBC nên $IJ//SB\Rightarrow IJ//\left( SBD \right).$

c) Do $M=AI\cap BO$ nên M là trọng tâm $\Delta ABC$

$\Rightarrow BM=\frac{2}{3}BO=\frac{BD}{3}$

Lại có: $SK=\frac{1}{2}KD\Leftrightarrow SK=\frac{1}{2}SD$ hay $\frac{SK}{SD}=\frac{1}{3}.$

Do đó $\frac{SK}{SD}=\frac{BM}{BD}=\frac{1}{3}\Rightarrow MK//SB\Rightarrow MK//\left( SBC \right).$

Lời giải chi tiết

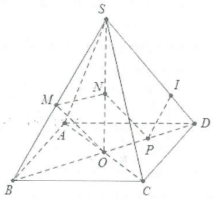
a) Do M, N lần lượt là trung điểm của SB,SO.

Do đó MN là đường trung bình của tam giác SBO nên

$MN//BO\Rightarrow MN//\left( ABCD \right).$

Tương tự MO là đường trung bình của tam giác SBD nên $MO//SD\Rightarrow MO//\left( SCD \right).$

b) NP là đường trung bình của tam giác SOD nên $NP//SD\Rightarrow NP//\left( SAD \right).$

Tứ giác NPOM là hình bình hành vì $MN//OP$ và $MN=OP=\frac{1}{2}OB.$

c) Ta có $\frac{SD}{ID}=\frac{BD}{PD}=4\Rightarrow IP//SB\Rightarrow IP//\left( SBC \right).$

Lời giải chi tiết

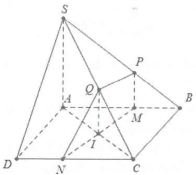
a) Trong mặt phẳng (SAB), qua M kẻ đường thẳng song song với SA, cắt SB tại P.

Trong mặt phẳng (ABCD) gọi $I=MN\cap AC.$

Trong mặt phẳng (SAC) kẻ đường thẳng song song với SA, cắt SC tại Q, ta có $\left( SAC \right)\cap \left( P \right)=IQ$

$\left( SAB \right)\cap \left( Q \right)=MP.$

b) Thiết diện là tứ giác MNQP.

c) Thiết diện là hình thang khi $QP//MN.$

Mặt khác ba mặt phẳng (SBC); (ABCD); (MNP) cắt nhau theo 3 giao tuyến là PQ, MN và BC nên chúng song song hoặc đồng quy.

Để $QP//MN\Rightarrow MN//BC//PQ$. Vậy $MN//BC$ thì thiết diện là hình thang.

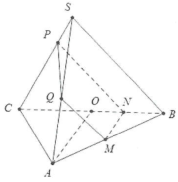
Lời giải chi tiết

a) Trong mặt phẳng (SAB), từ M kẻ đường thẳng song song với SB, cắt SB tại Q.

Trong mặt (ABC), từ M kẻ đường thẳng song song với AO, cắt BC tại N.

Trong mặt phẳng (SBC), từ N kẻ đường thẳng song song với SB, cắt SC tại P.

Thiết diện là tứ giác MNPQ.

Ta có: $\left\{ \begin{array}  {} MN//AO \\  {} MQ//SB \\  {} SB\bot OA\text{ } \\ \end{array} \right.\Rightarrow MN\bot MQ\Rightarrow$ thiết diện là hình thang vuông tại M và N.

b) Áp dụng định lý Talet ta có: $BM=x\Rightarrow MA=a-x\Rightarrow \frac{MQ}{SB}=\frac{MQ}{a}=\frac{MA}{AB}=\frac{a-x}{a}\Rightarrow MQ=a-x$

$BC=2a\Rightarrow OA=\frac{1}{2}BC=a\Rightarrow \frac{MN}{OA}=\frac{MN}{a}=\frac{BM}{AB}=\frac{x}{a}\Rightarrow MN=x$

$\frac{BN}{BO}=\frac{MN}{OA}\Rightarrow BN=MN=x\Rightarrow NC=2a-x\Rightarrow \frac{NP}{SB}=\frac{NP}{a}=\frac{NC}{BC}=\frac{2a-x}{2a}\Rightarrow NP=\frac{2a-x}{2}$

${{S}_{MNPQ}}=\frac{1}{2}MN\left( MQ+NP \right)=\frac{1}{2}x.\left( a-x+\frac{2a-x}{2} \right)=\frac{x\left( 4a-3x \right)}{4}$

Do đó áp dụng bất đẳng thức $uv\le {{\left( \frac{u+v}{2} \right)}^{2}}$ ta có:

${{S}_{MNPQ}}=\frac{x\left( 4a-3x \right)}{4}=\frac{3x\left( 4a-3x \right)}{12}\le \frac{{{\left( 3x+4a-3x \right)}^{2}}}{12.4}=\frac{1}{3}{{a}^{2}}.$

Dấu đẳng thức xảy ra khi và chỉ khi $3x=4a-3x\Leftrightarrow 6x=4a\Leftrightarrow x=\frac{2a}{3}.$

Lời giải chi tiết

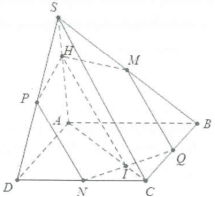
a) Trong mặt phẳng (SBC), từ M kẻ đường thẳng song song với SC cắt BC tại Q.

Trong mặt phẳng (SCD), từ N kẻ đường thẳng song song với SC cắt SD tại P.

Khi đó giao tuyến của (P) với (SBC) và (SCD) lần lượt là MQ và NP.

Gọi $I=AC\cap NQ$. Từ I kẻ đường thẳng song song với SC cắt SA tại H.

Khi đó $\left( P \right)\cap \left( SAC \right)=IH.$

b) Thiết diện của mặt phẳng (P) với khối chóp là ngũ giác MQNPH.

Lời giải chi tiết

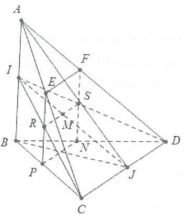
a) Mặt phẳng (P) qua M và song song với CD nên giao tuyến của (P) và (ICD) cũng song song với CD.

Trong mặt phẳng (ICD), qua M kẻ đường thẳng $d//CD$ cắt IC và ID lần lượt tại R và S khi đó giao tuyến của (P) với (ICD) là RS.

b) Qua R và (S) lần lượt kẻ các đường thẳng song song với SA cắt các cạnh bên AC, BC, BD, AD lần lượt tại E, P, N, F khi đó thiết diện của tứ diện ABCD với (P) là tứ giác EFNP.