Đồ thị dao động điều hòa là gì?

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

Lý thuyết trọng tâm:

- Phương trình dao động điều hòa có dạng theo hàm cosin: $x=A\cos \left( \omega t+\varphi \right)$

- Khi đó phương trình vận tốc của vật: $v=\omega A\cos \left( \omega t+\varphi +\frac{\pi }{2} \right)$

- Phương trình gia tốc của vật: $a={{\omega }^{2}}A\cos \left( \omega t+\varphi +\pi \right)$

Phương pháp giải:

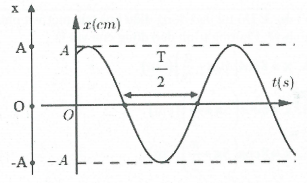
+) Xác định biên độ dao động.

+) Dựa vào giao điểm của đồ thị với trục đứng Ox để tìm trạng thái ban đầu của vật $\left\{ \begin{array}{} x? \\ {} v? \\ \end{array} \right.\Rightarrow {{\varphi }_{0}}$

(Nếu dựa vào đường tròn để tìm pha ban đầu ${{\varphi }_{0}}$)

+) Dựa vào giao điểm của đồ thị với trục ngang Ot để xác định chu kì T và tần số góc $\omega $