Điện xoay chiều có 1 phần tử là gì?

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI
1. Mạch điện xoay chiều chỉ có điện trở
Tổng quát:
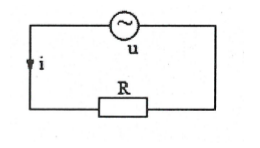 Đặt điện áp xoay chiều $u={{\mathsf{U}}_{0}}\cos (\omega t+\varphi )$ vào hai đầu đoạn mạch chỉ có R
Đặt điện áp xoay chiều $u={{\mathsf{U}}_{0}}\cos (\omega t+\varphi )$ vào hai đầu đoạn mạch chỉ có R
Theo định luật Ôm ta có: $i=\frac{u}{R}=\frac{U}{R}\sqrt{2}\cos (\omega t+\varphi )$
Đặt $I=\frac{U}{R}$ suy ra$i=I\sqrt{2}\cos \left( \omega t+\varphi \right)={{I}_{0}}\cos \left( \omega t+\varphi \right)$
Đặc điểm :
+) Trong mạch điện xoay chiều chỉ có điện trở ta có: u và i cùng pha $({{\varphi }_{u}}={{\varphi }_{i}})$
+) Cường độ dòng điện: $I=\frac{U}{R};{{I}_{0}}=\frac{{{U}_{0}}}{R}$
 +) Giản đồ vecto:
+) Giản đồ vecto:
2. Mạch điện xoay chiều chỉ có tụ điện.
Tổng quát:
Đặt điện áp xoay chiều $u={{U}_{0}}\cos \left( \omega t+\varphi \right)$ vào hai đầu đoạn mạch chỉ có tụ điện C
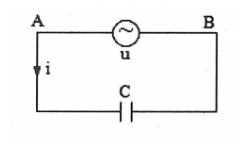 Điện tích trên bản tụ điện: $q=Cu=CU\sqrt{2}\cos \left( \omega t+\varphi \right)$
Điện tích trên bản tụ điện: $q=Cu=CU\sqrt{2}\cos \left( \omega t+\varphi \right)$
Lại có: $i=\frac{dq}{dt}=q'\left( t \right)=-\omega CU\sqrt{2}\sin \left( \omega t+\varphi \right)$
Hay $i=\omega CU\sqrt{2}\cos \left( \omega t+\varphi +\frac{\pi }{2} \right)$
Đặt $I=\omega CU$ ta có: $i=I\sqrt{2}\cos \left( \omega t+\varphi +\frac{\pi }{2} \right)$ và $u=U\sqrt{2}\cos \left( \omega t+\varphi \right)$
Đặc điểm:
+) Trong mạch điện xoay chiều chỉ có tụ điện thì: u chậm pha hơn i góc$\frac{\pi }{2}$ hay ${{\varphi }_{i}}={{\varphi }_{u}}+\frac{\pi }{2}$
+) Định luật Ôm. Ta có: $U\omega C=I\Leftrightarrow \frac{U}{I}=\frac{1}{C\omega }={{Z}_{C}}$
$Z_{C}^{{}}$ được gọi là dung kháng của tụ điện, đơn vị tính:Ôm $\left( \Omega \right)$ .
Suy ra: ${{Z}_{C}}=\frac{1}{C\omega }=\frac{1}{C2\pi f},{{Z}_{C}}=\frac{{{U}_{C}}}{I}=\frac{{{U}_{0C}}}{{{I}_{0}}}$
Ý nghĩa của dung kháng
-$Z_{C}^{{}}$ là đại lượng biểu hiện sự cản trở dòng điện xoay chiều của tụ điện
-Dòng điện xoay chiều có tần số cao (cao tần) chuyển qua tụ điện dễ dàng hơn dòng điện xoay chiều tần số thấp
-${{Z}_{C}}$ cũng có tác dụng làm cho i sớm pha $\frac{\pi }{2}$ so với u
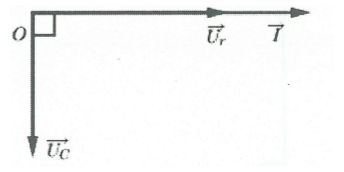 +) Giản đồ vecto
+) Giản đồ vecto
Chú ý: Do ${{u}_{C}}\bot i$ nên ta có:${{\left( \frac{u}{{{U}_{0}}} \right)}^{2}}+{{\left( \frac{i}{{{I}_{0}}} \right)}^{2}}=1\Rightarrow {{\left( \frac{u}{U} \right)}^{2}}+{{\left( \frac{i}{I} \right)}^{2}}=2$
Tại hai thời điểm ${{t}_{1}}$ và ${{t}_{2}}$ ta có: $\frac{{{u}_{1}}^{2}}{{{U}_{0}}^{2}}+\frac{{{i}_{1}}^{2}}{{{I}_{0}}^{2}}=\frac{{{u}_{2}}^{2}}{{{U}_{0}}^{2}}+\frac{{{i}_{2}}^{2}}{{{I}_{0}}^{2}}\Rightarrow \frac{{{U}_{0}}}{{{I}_{0}}}=\sqrt{\frac{{{u}_{1}}^{2}-{{u}_{2}}^{2}}{{{i}_{2}}^{2}-{{i}_{1}}^{2}}}={{Z}_{C}}$
Công thức tính điện dung của tụ phẳng:
$C=\frac{\varepsilon S}{{{9.10}^{9}}.4\pi d}$
$\varepsilon $ : Hằng số điện môi
S : Phần thể tích giữa 2 bản tụ $\left( {{m}^{3}} \right)$
d : Khoảng cách giữa hai bản tụ (m)
-Điện môi bị đánh thủng là hiện tượng khi điện trường tăng vượt qua một giá trị giới hạn nào đó sẽ làm cho điện môi mất tính cách điện
-Điện áp giới hạn là điện áp lớn nhất mà điện môi không bị đánh thủng
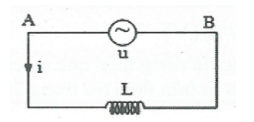 3. Mạch điện xoay chiều chỉ có cuộn cảm thuần
3. Mạch điện xoay chiều chỉ có cuộn cảm thuần
Tổng quát:
Đặt điện áp xoay chiều $u={{U}_{0}}\cos \left( \omega t+\varphi \right)$ vào
hai đầu đoạn mạch chỉ có cuộn thuần cảm L
Tương tự như trên ta suy ra một số đặc điểm của mạch
Đặc điểm:
+) Trong mạch điện xoay chiều chỉ có cuộn thuần cảm thì: u nhanh pha hơn i góc$\frac{\pi }{2}$ hay ${{\varphi }_{u}}={{\varphi }_{i}}+\frac{\pi }{2}$
+) Định luật Ôm. Ta có: $U=I.L.\omega \Leftrightarrow \frac{U}{I}=L\omega ={{Z}_{L}}$
${{Z}_{L}}$ được gọi là cảm kháng của cảm kháng, đơn vị tính: Ôm $\left( \Omega \right)$
Suy ra ${{Z}_{L}}=L.\omega =L.2\pi .f,{{Z}_{L}}=\frac{{{U}_{L}}}{I}=\frac{{{U}_{0L}}}{{{I}_{0}}}$
Ý nghĩa của cảm kháng
-${{Z}_{L}}$ là đại lượng biểu hiện sự cản trở dòng điện xoay chiều của cuộn cảm
- Cuộn cảm có L lớn sẽ cản trở nhiều đối với dòng điện xoay chiều, nhất là dòng điện xoay chiều cao tần
-${{Z}_{L}}$ cũng có tác dụng làm cho i trễ pha $\frac{\pi }{2}$ so với u
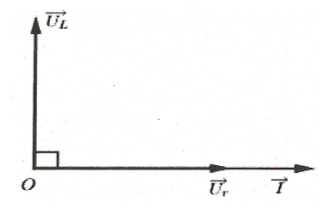 +) Giản đồ vecto
+) Giản đồ vecto
Chú ý: Do ${{u}_{L}}\bot i$ nên ta có:x 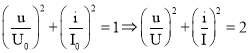
Tại hai thời điểm ![]() và
và ![]() ta có:
ta có: 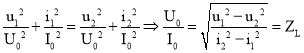
Lưu ý các trường hợp mạch ghép R hoặc L hoặc C:
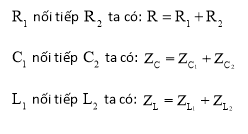
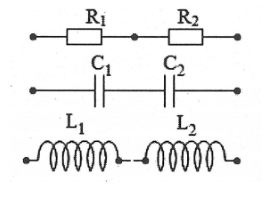
Bài tập minh họa:
|
Bài tập minh họa 1: Mắc điện trở thuần a) Viết biểu thức cường độ dòng điện qua mạch b) Tính nhiệt lượng tỏa ra trên điện trở trong 20 phút |
Lời giải chi tiết
a) Ta có ![]()
Do mạch chỉ có R nên u và i cùng pha. Khi đó ![]()
b) Nhiệt lượng tỏa ra trên điện trở R trong 10 phút là:
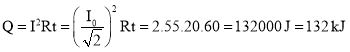
|
Bài tập minh họa 2: Đặt điện áp |
Lời giải chi tiết
Mạch chỉ có tụ điện nên điện áp chậm pha hơn dòng điện góc ![]() , khi đó
, khi đó ![]()
Dung kháng của mạch là ![]()
Áp dụng hệ thức liên hệ ta được 
Vậy cường độ dòng điện chạy qua bản tụ điện có biểu thức ![]()
VẬT LÝ LỚP 12
