Dao động cùng pha ngược pha là gì?

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

Phương pháp chung:

Phương trình sóng tại 2 nguồn cùng biên độ A:

(Điểm M cách hai nguồn lần lượt là ${{d}_{1}};{{d}_{2}}$):

${{u}_{1}}=A\cos \left( 2\pi ft+{{\varphi }_{1}} \right)$ và ${{u}_{2}}=A\cos \left( 2\pi ft+{{\varphi }_{2}} \right)$

Phương trình sóng tại M do hai sóng từ nguồn truyền tới: ${{u}_{1M}}=A\cos \left( 2\pi ft-2\pi \frac{{{d}_{1}}}{\lambda }+{{\varphi }_{1}} \right)$ và ${{u}_{2M}}=A\cos \left( 2\pi ft-2\pi \frac{{{d}_{2}}}{\lambda }+{{\varphi }_{2}} \right)$

Phương tình giao thoa sóng tại M: ${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}$

${{u}_{M}}=2A\cos \left[ \pi \frac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\frac{\Delta \varphi }{2} \right]\cos \left[ 2\pi ft-\pi \frac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\frac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right]$

Từ đó suy ra pha dao động của điểm M.

Điểm M dao động cùng pha với nguồn 1 khi ${{\varphi }_{M}}-{{\varphi }_{1}}=k2\pi $.

Điểm M dao động ngược pha với nguồn 1 khi ${{\varphi }_{M}}-{{\varphi }_{1}}=\left( 2k+1 \right)\pi $.

Với dạng toán này ta xét một số trường hợp sau:

Dạng 1: Các điểm dao động cùng pha, ngược pha trên đường trung trực.

Bài toán:

Tìm điểm M thuộc đường trung trực của AB, dao động cùng pha, ngược pha so với điểm A (B, trung điểm của AB ....).

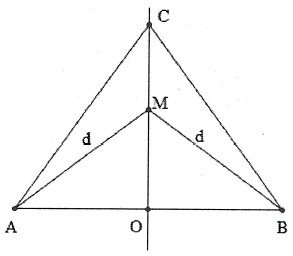
Phương pháp giải:

TH1: Hai nguồn A, B dao động cùng pha với nhau

Giả sử ${{u}_{A}}=a\cos \left( \omega t \right),{{u}_{B}}=b\cos \left( \omega t \right)$

Khi đó: ${{u}_{AM}}=a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right);$

${{u}_{BM}}=b\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)$

$\Rightarrow {{u}_{M}}=\left( a+b \right)\cos \left( \omega t-\frac{2\pi .d}{\lambda } \right)$

PT tại O: ${{u}_{O}}=\left( a+b \right)\cos \left( \omega t-\frac{2\pi .OA}{2} \right)$.

Suy ra: Độ lệch pha giữa M và A và B là: $\Delta {{\varphi }_{M/A,B}}=\frac{2\pi d}{\lambda }.$

Độ lệch pha giữa M so với O là: $\Delta {{\varphi }_{M/O}}=\frac{2\pi \left( d-OM \right)}{\lambda }.$

Như vậy:

+) Điểm M dao động cùng pha với A (hoặc B) khi: $\frac{2\pi d}{\lambda }=k2\pi \Leftrightarrow d=k\lambda $.

+) Điểm M dao động cùng pha với điểm O khi: $d-OM=k\lambda \Rightarrow d=OM+k\lambda $.

+) Điểm M dao động ngược pha với A khi: $d=\left( k+0,5 \right)\lambda $.

+) Điểm M dao động ngược pha với O khi: $d-OM=\left( k+0,5 \right)\lambda \Rightarrow d=OM+\left( k+0,5 \right)\lambda $.

TH2: Hai nguồn A, B dao động ngược pha: Giả sử: ${{u}_{A}}=a\cos \left( \omega t+\pi \right),{{u}_{B}}=b\cos \left( \omega t \right)$

Khi đó: ${{u}_{AM}}=a\cos \left( \omega t+\pi -\frac{2\pi d}{\lambda } \right)$ và ${{u}_{BM}}=b\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)$

Suy ra ${{u}_{M}}={{u}_{AM}}+{{u}_{BM}}=-a\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)+b\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)=\left( b-a \right)\cos \left( \omega t-\frac{2\pi d}{\lambda } \right)$.

Với $b=a$ thì điểm M không dao động (ta không xét).

Với $b>a$ thì ${{\varphi }_{M}}=-\frac{2\pi d}{\lambda }$.

Với $b<a$ thì ${{\varphi }_{M}}=\pi -\frac{2\pi d}{\lambda }$.

Dạng 2: Các điểm dao động CĐ, CT đồng thời cùng pha, ngược pha với nguồn trên AB.

Cách 1:

Xét 2 nguồn: ${{u}_{A}}={{u}_{B}}=a\cos \left( \omega t \right)\Rightarrow \left\{ \begin{array}{} {{u}_{AM}}=a\cos \left( \omega t-\frac{2\pi AM}{\lambda } \right) \\ {} {{u}_{BM}}=a\cos \left( \omega t-\frac{2\pi BM}{\lambda } \right) \\ \end{array} \right.$

Do đó ${{u}_{M}}={{u}_{AM}}+{{u}_{BM}}=2a\cos \left( \omega t-\frac{\pi .AB}{\lambda } \right)\cos \frac{\pi \left( MA-MB \right)}{\lambda }$.

Để tồn tại cực đại, cực tiểu đồng thời cùng pha, ngược pha với nguồn thì $AB=n\lambda $.

Khi đó: ${{u}_{M}}=2a\cos \left( \omega t-n\pi \right)\cos \frac{\pi \left( MA-MB \right)}{\lambda }$.

Nếu n chẵn thì cực đại cùng pha với nguồn khi $MA-MB=2k\lambda $.

Nếu n lẻ thì cực đại cùng pha với nguồn khi: $MA-MB=\left( 2k+1 \right)\lambda $.

Cách 2:

Vẽ hình và đếm

þ Cực đại cùng pha (ngược pha) với nguồn.

Để tồn tại cực đại, cực tiểu đồng thời cùng pha, ngược pha với nguồn thì $AB=n\lambda $.

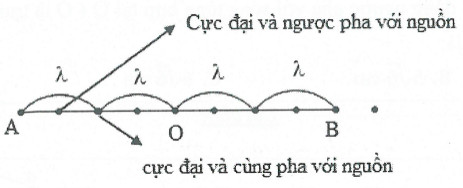
þ Cực đại cùng pha (ngược pha) với trung điểm của AB.

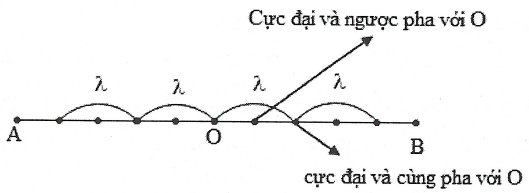
+) Các điểm dao động cùng pha cách nhau $k\lambda .$.

+) Các điểm dao động ngược pha cách nhau $\left( k+0,5 \right)\lambda $.

+) Các điểm cực đại cách nhau $d=\frac{\lambda }{2}$, các điểm cực tiểu cách nhau $d=\frac{\lambda }{2}$.