Cưc đại và cực tiểu là gì? Cách xác định điểm cực trị của hàm số

Cưc đại và cực tiểu là gì? Cách xác định điểm cực trị của hàm số

 Định nghĩa điểm cực đại cực tiểu

Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên khoảng $\left( a;b \right)$ (có thể $a$ là $-\infty $; $b$ là $+\infty $) và điểm ${{x}_{0}}\in \left( a;b \right)$

a) Nếu tồn tại số $h>0$ sao cho $f\left( x \right)<f\left( {{x}_{0}} \right)$ với mọi $x\in \left( {{x}_{0}}-h;{{x}_{0}}+h \right)$ và $x\ne {{x}_{0}}$ thì ta nói hàm số $f\left( x \right)$ đạt cực đại tại ${{x}_{0}}$.

b) Nếu tồn tại số $h>0$ sao cho $f\left( x \right)>f\left( {{x}_{0}} \right)$ với mọi $x\in \left( {{x}_{0}}-h;{{x}_{0}}+h \right)$ và $x\ne {{x}_{0}}$ thì ta nói hàm số $f\left( x \right)$ đạt cực tiểu tại ${{x}_{0}}$.

Chú ý về điểm cực trị

- Nếu hàm số $f\left( x \right)$đạt cực đại (cực tiểu) tại điểm ${{x}_{0}}$ thì ${{x}_{0}}$được gọi là điểm cực đại (điểm cực tiểu) của hàm số; $f\left( {{x}_{0}} \right)$ được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, ký hiệu là ${{f}_{CD}}\left( {{f}_{CT}} \right)$, còn điểm $M\left( {{x}_{0}};f\left( {{x}_{0}} \right) \right)$ được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.

- Các điểm cực đại cực tiểu được gọi chung là điểm cực trị.

- Dễ dàng chứng minh được rằng, nếu hàm số $y=f\left( x \right)$ có đạo hàm trên khoảng $\left( a;b \right)$ và đạt cực đại hoặc cực tiểu tại ${{x}_{0}}$ thì $f'\left( {{x}_{0}} \right)=0.$

 Định lý 1: Giả sử hàm số $y=f\left( x \right)$liên tục trên khoảng $K=\left( {{x}_{0}}-h;{{x}_{0}}+h \right)$ và có đạo hàm trên $K$ hoặc trên $K\backslash \left\{ {{x}_{0}} \right\},$ với $h>0$.

- Nếu $f'\left( {{x}_{0}} \right)>0$ trên khoảng $\left( {{x}_{0}}-h;{{x}_{0}} \right)$và $f'\left( {{x}_{0}} \right)<0$ trên khoảng $\left( {{x}_{0}};{{x}_{0}}+h \right)$ thì ${{x}_{0}}$ là điểm cực đại của hàm số $f\left( x \right).$

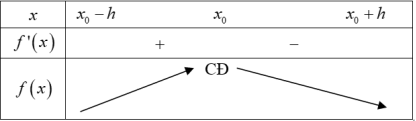
- Nếu $f'\left( {{x}_{0}} \right)<0$ trên khoảng $\left( {{x}_{0}}-h;{{x}_{0}} \right)$và $f'\left( {{x}_{0}} \right)>0$ trên khoảng $\left( {{x}_{0}};{{x}_{0}}+h \right)$ thì ${{x}_{0}}$ là điểm cực tiểu của hàm số $f\left( x \right).$

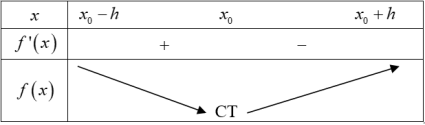
Nhận xét: Xét hàm số $y=f\left( x \right)$ liên tục và xác định trên $\left( a;b \right)$ và ${{x}_{0}}\in \left( a;b \right).$

- Nếu $f'\left( x \right)$ đổi dấu khi qua điểm ${{x}_{0}}$ thì ${{x}_{0}}$ là điểm cực trị của hàm số.

- Nếu $f'\left( x \right)$ đổi dấu từ dương sang âm khi qua điểm ${{x}_{0}}$ thì ${{x}_{0}}$ là điểm cực đại của hàm số.

- Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương khi qua điểm ${{x}_{0}}$ thì ${{x}_{0}}$ là điểm cực tiểu của hàm số.

Chú ý: Hàm số $y=\sqrt{{{x}^{2}}}=\left| x \right|$ có đạo hàm là $y'=\frac{2x}{2\sqrt{{{x}^{2}}}}$ không có đạo hàm tại điểm $x=0$ tuy nhiên $y'$ vẫn đổi dấu từ âm sang dương khi qua điểm $x=0$ nên hàm số đạt cực tiểu tại điểm $x=0$.

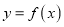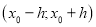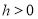 Định lý 2: Giả sử hàm số  có đạo hàm cấp hai trong khoảng   với  . Khi đó:

- Nếu $\left\{ \begin{matrix}   f'\left( {{x}_{0}} \right)=0  \\   f''\left( {{x}_{0}} \right)>0  \\\end{matrix} \right.\Rightarrow {{x}_{0}}$ là điểm cực tiểu.

- Nếu $\left\{ \begin{matrix}   f'\left( {{x}_{0}} \right)=0  \\   f''\left( {{x}_{0}} \right)<0  \\\end{matrix} \right.\Rightarrow {{x}_{0}}$ là điểm cực đại.

Chú ý: Nếu $f'\left( {{x}_{0}} \right)=0$ và $f''\left( {{x}_{0}} \right)=0$ thì chưa thể khẳng định được ${{x}_{0}}$ là điểm cực đại hay điểm cực tiểu hay cực trị của hàm số.

Bài tập: Hàm số $y={{x}^{3}}$ có $\left\{ \begin{matrix}   f'\left( 0 \right)=0  \\   f''\left( 0 \right)=0  \\\end{matrix} \right.$ tuy nhiên hàm số này không đạt cực trị tại điểm $x=0$.

Hàm số $y={{x}^{4}}$ có $\left\{ \begin{matrix}   f'\left( 0 \right)=0  \\   f''\left( 0 \right)=0  \\\end{matrix} \right.$ tuy nhiên hàm số này đạt cực tiểu tại điểm  .

Do vậy ta chú ý định lý 2 chỉ đúng theo một chiều (không có chiều ngược lại).