Công thức diện tích hình nón và thể tích khối nón

Công thức diện tích hình nón và thể tích khối nón

Một hình chóp gọi là nội tiếp hình nón nếu:

- Đáy của hình chóp là đa giác nội tiếp đáy của hình nón

- Đỉnh của hình chóp là đỉnh của hình nón

Định nghĩa.

Diện tích xung quanh của hình nón là giới hạn của diện tích xung quanh của một hình chóp đều nội tiếp hình nón đó khi số cạnh đáy tăng lên vô hạn

Thể tích của khối nón là giới hạn của thể tích khối chóp đều nội tiếp khối nón đó khi số cạnh tăng lên vô hạn

Diện tích xung quanh, diện tích toàn phần của hình nón

Diện tích xung quanh: ${{S}_{xq}}=\pi Rl$

Diện tích toàn phần: ${{S}_{tp}}={{S}_{xq}}+{{S}_{}}=\pi Rl+\pi {{R}^{2}}$

Trong đó , R, l lần lượt là bán kính đáy và đường sinh của hình nón

Thể tích của khối nón

Thể tích của khối nón có bán kính đáy R và chiều cao h là $V=\frac{1}{3}\pi {{R}^{2}}h$

Mối liên hệ giữa chiều cao, đường sinh và bán kính đáy

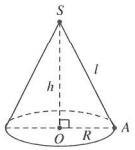
Tam giác SAO vuông tại A, có $S{{A}^{2}}=S{{O}^{2}}+O{{A}^{2}}$

Do đó (tham khảo hình vẽ bên)

Vị trí tương đối của hình nón với một mặt phẳng qua đỉnh của nó

Cho một hình nón (N) và một mặt phẳng (P) đi qua đỉnh S của hình nón.

Có ba vị trí tương đối giữa (P) và (N)

l (P) và (N) có một điểm chung duy nhất

l (P) và (N) có chung một đường sinh duy nhất. Khi đó (P) tiếp xúc với (N) và (P) gọi là tiếp diện của (N)

l (P) và (N) có chung hai đường sinh (Hình 1). Nếu (P) chứa trục của hình nón thì thiết diện của (P) và hình nón gọi là thiết diện qua trục (Hình 2)

l Thiết diện qua trục của hình nón là tam giác cân có cạnh bên SA = l, cạnh đáy AB = 2R