Công thức cắt ghép lò xo

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

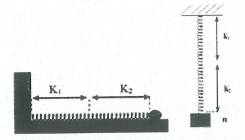
1. Cắt, ghép lò xo

Thay đổi độ cứng của con lắc lò xo.

Độ cứng của lò xo phụ thuộc vào chất liệu cấu tạo nên lò xo, chiều dài và tiết diện của lò xo.

Ta có: $k=\frac{ES}{\ell }$ trong đó E là suất Y-âng đặc trưng cho vật liệu cấu tạo nên lò xo, S là tiết diện lò xo và $\ell $ là chiều dài lò xo.

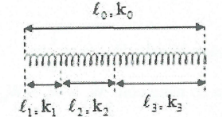
Suy ra $k.\ell =E.S=const$ như vậy với một lò xo xác định thì $k.\ell $ là một hằng số.

Cắt lò xo:

Khi cắt một lò xo thành các phần có chiều dài

${{\ell }_{1}};{{\ell }_{2}}...;{{\ell }_{n}}$ ta có:

$k\ell ={{k}_{1}}{{\ell }_{1}}={{k}_{2}}{{\ell }_{2}}...={{k}_{n}}{{\ell }_{n}}$ (lò xo càng ngắn càng cứng).

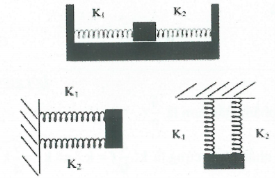
Ghép lò xo

Con lắc lò xo ghép nối tiếp:

$\frac{1}{k}=\frac{1}{{{k}_{1}}}+\frac{1}{{{k}_{2}}}+...\frac{1}{{{k}_{n}}}\Rightarrow {{T}^{2}}=T_{1}^{2}+T_{2}^{2}+...+T_{n}^{2}$

Con lắc lò xo ghép song song:

$k={{k}_{1}}+{{k}_{2}}+...{{k}_{n}}\Rightarrow \frac{1}{{{T}^{2}}}=\frac{1}{T_{1}^{2}}+\frac{1}{T_{2}^{2}}+...+\frac{1}{T_{n}^{2}}$.

2. Giữ lò xo

a. ĐẶT VẤN ĐỀ:

Xét bài toán: Một con lắc lò xo nằm ngang có độ cứng k, vật nặng m, dao động với biên độ A.

Tại VTCB lò xo dài $\ell $. Khi vật ở li độ x, người ta giữ chặt lò xo tại vị trí cách điểm cố định một đoạn bằng n lần chiều dài lò xo hiện tại. Hỏi biên độ mới của con lắc là bao nhiêu?

b. Phương pháp giải:

Do phần còn lại của lò xo dài chỉ còn $\left( 1-n \right)\left( \ell +x \right)$.

Độ cứng mới của lò xo: $\frac{k}{1-n}$

Chiều dài tự nhiên mới của lò xo: $\left( 1-n \right)\ell $.

Suy ra li độ của vật so với hệ mới: ${x}'=\left( 1-n \right)x$

Cách 1:

Áp dụng công thức liên hệ để ý vận tốc 2 trường hợp là bằng nhau và ${\omega }'=\sqrt{\frac{{{k}'}}{m}}$ ta có:

$\left\{ \begin{array}{} {{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}={{A}^{2}} \\ {} {{{{x}'}}^{2}}+\frac{{{v}^{2}}}{{{{{\omega }'}}^{2}}}={{{{A}'}}^{2}} \\ \end{array} \right.$. Từ đó giải hệ suy ra ${A}'$.

Cách 2:

Sử dụng định luật bảo toàn cơ năng:

Cơ năng ban đầu: ${{\text{W}}_{0}}=\frac{1}{2}k{{A}^{2}}$.

Do thế năng của lò xo phân bố đều trên cả lò xo nên ta giữ n lần chiều dài lò xo thế năng sẽ mất đi n lần.

Thế năng bị mất: ${{\text{W}}_{loss}}=n.\frac{1}{2}k{{x}^{2}}$

Suy ra cơ năng còn:${{\text{W}}_{c}}={{\text{W}}_{0}}-{{\text{W}}_{loss}}$ đây sẽ là cơ năng toàn phần của con lắc mới.

Cơ năng của con lắc mới: ${{\text{W}}_{2}}=\frac{1}{2}.{k}'{{{A}'}^{2}}$.

Ta có ${{\text{W}}_{c}}={{\text{W}}_{2}}$ giải phương trình này ta tìm được ${A}'$.

Đặc biệt: Khi giữ lò xo lúc vật đang ở vị trí cân bằng thì thế năng bị mất:

${{\text{W}}_{loss}}=n.\frac{1}{2}k{{x}^{2}}=0\Rightarrow \frac{1}{2}k{{A}^{2}}=\frac{1}{2}{k}'{{{A}'}^{2}}\Rightarrow {A}'=A\sqrt{\frac{k}{{{k}'}}}$.