Công suất và hệ số công suất là gì?

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI.

1. Công suất của mạch điện xoay chiều

Biểu thức của công suất:

Xét mạch điện xoay chiều hình sin.

Điện áp tức thời hai đầu mạch: $u=U\sqrt{2}\cos \omega t$.

Cường độ dòng điện tức thời trong mạch: $i=I\sqrt{2}\cos (\omega t+\varphi )$

Công suất tiêu thụ trong mạch tại thời điểm t là: p=ui.

Đại lượng p được gọi là công suất tức thời của mạch điện xoay chiều:

$p=ui=2UI\cos \omega t.\cos (\omega t+\varphi )=UI.\left[ cos\varphi +\cos (2\omega t+\varphi ) \right]$,

Khi đó công suất điện tiêu thụ trong một chu kì T là:

$P=\overline{p}=UI\left[ \overline{cos\varphi }+\overline{\cos (2\omega t+\varphi )} \right]$.

Do giá trị trung bình của $\cos (2\omega t+\varphi )$ bằng không trong khoảng thời gian T.

Ta được giá trị trung bình của công suất điện tiêu thụ trong một chu kì là:

$$.

Nếu thời gian dùng điện t rất lớn so với $T(t\gg T)$ thì P cũng là công suất điện tiêu thụ trung bình của mạch điện trong thời gian đó (nếu U và I không thay đổi).

Điện năng tiêu thụ của mạch điện:

Điện năng tiêu thụ của mạch điện trong thời gian t là: W=Pt.

2. Hệ số công suất.

Định nghĩa: Ta có: $P=UI\cos \varphi $, khi đó $\cos \varphi $ được gọi là hệ số công suất.

Khi đó: $\cos \varphi =\frac{P}{UI}$.

3. Tính hệ số công suất của mạch điện.

+) Mạch chỉ có điện trở: $\cos \varphi =\frac{R}{Z}=\cos 0=1$.

+) Mạch chỉ có tụ điện hoặc chỉ có cuộn dây thuần cảm: $\cos \varphi =0.$

(Mạch không tiêu thụ công suất)

+) Mạch R - L gồm điện trở thuần và cuộn thuần cảm: $\cos \varphi =\frac{R}{\sqrt{{{R}^{2}}+Z_{L}^{2}}}=\frac{R}{\sqrt{{{R}^{2}}+{{(L\omega )}^{2}}}}.$

+) Mạch R – C gồm điện trở thuần và tụ điện: $\cos \varphi =\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}}=\frac{R}{\sqrt{{{R}^{2}}+\frac{1}{{{C}^{2}}{{\omega }^{2}}}}}.$

+) Với mạch tổng quát R-L-C nối tiếp ta có:

$\cos \varphi =\frac{{{U}_{R}}}{U}=\frac{R}{Z}=\frac{R}{\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}}.$

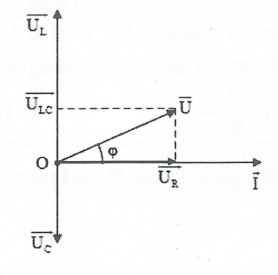
Công suất trung bình tiêu thụ trong một mạch điện xoay chiều bất kỳ được tính bời:

$P=UI\cos \varphi =U.\frac{U}{Z}.\frac{R}{Z}=R{{\left( \frac{U}{Z} \right)}^{2}}=R{{I}^{2}}$

$=RI.I={{U}_{R}}.I.$

Vậy, Công suất tiêu thụ trong mạch điện có R,L,C mắc nối tiếp bằng công suất tỏa nhiệt trên R.

4. Bài tập minh họa:

HD giải:

a) Tổng trở và độ lệch pha của u, i trong mạch là

$\left\{ \begin{array}{*{35}{l}}Z=60\Omega \\\varphi =\frac{\pi }{6}-\frac{\pi }{3}=-\frac{\pi }{6} \\\end{array} \right.\Rightarrow \left\{ \begin{array}{*{35}{l}}{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}={{60}^{2}} \\\tan \left( -\frac{\pi }{6} \right)=\frac{{{Z}_{L}}-{{Z}_{C}}}{R}=-\frac{1}{\sqrt{3}} \\\end{array} \right.$

Giải hệ trên ta được $R=30\sqrt{3}\Omega $

b) Công suất tiêu thụ của đoạn mạch là $P=UI.\cos \varphi =120.2.\cos \left( -\frac{\pi }{6} \right)=120\sqrt{3}$W.

c) Điện năng tiêu thụ trong 1 giờ (hay 3600s) là $W=P.t=120\sqrt{3}.3600=432\sqrt{3}$kJ.