Chứng minh các đằng thức vectơ, chứng minh 3 vectơ đồng phẳng – Bài tập có đáp án chi tiết

Chứng minh các đằng thức vectơ, chứng minh 3 vectơ đồng phẳng – Bài tập có đáp án
Phương pháp giải chứng minh các đẳng thức vecto đồng phẳng
Để chứng minh ba vectơ đồng phẳng, ta có thể chứng mình bằng một trong các cách:
| – Chứng minh các giá của ba vectơ cùng song song với một mặt phẳng.
– Dựa vào điều kiện để ba vectơ đồng phẳng: tồn tai các số m. n duy nhất sao cho $\overrightarrow{c}=m.\overrightarrow{a}+n.\overrightarrow{b}$ thì 3 vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ đồng phẳng. Để biểu diễn vectơ $\overrightarrow{x}$ theo 3 vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ không đồng phẳng ta tìm được các số m, n, p duy nhất sao cho $\overrightarrow{x}=m.\overrightarrow{a}+n.\overrightarrow{b}+p.\overrightarrow{c}$ |
Bài tập chứng minh các đẳng thức vecto, chứng minh 3 vecto đồng phẳng có đáp án chi tiết
| Bài tập 1: Cho tứ diện ABCD. Gọi I và J là trung điểm của AB và CD.
a) Hãy biểu diễn vectơ $\overrightarrow{IJ}$ theo 3 vectơ $\overrightarrow{AB}$, $\overrightarrow{AC}$, $\overrightarrow{AD}$ b) Gọi G là trọng tâm tam giác BCD. Hãy biểu diễn vectơ $\overrightarrow{AG}$ theo 3 vectơ $\overrightarrow{AB}$, $\overrightarrow{AC}$, $\overrightarrow{AD}$ |
Lời giải chi tiết
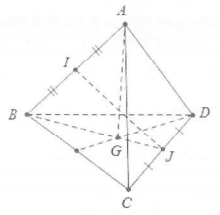
a) Ta có: $\overrightarrow{IJ}=\left( \overrightarrow{IA}+\overrightarrow{AJ} \right)$, mặt khác $\overrightarrow{IA}=-\overrightarrow{AI}=-\frac{1}{2}\overrightarrow{AB}$
$\overrightarrow{AJ}=\frac{1}{2}\left( \overrightarrow{AC}+\overrightarrow{AD} \right)$(tính chất trung điểm)
Do đó $\overrightarrow{IJ}=-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{AD}$
b) Ta có: $\left\{ \begin{array} {} \overrightarrow{AB}=\overrightarrow{AG}+\overrightarrow{GB} \\ {} \overrightarrow{AC}=\overrightarrow{AG}+\overrightarrow{GC} \\ {} \overrightarrow{AD}=\overrightarrow{AG}+\overrightarrow{GD} \\ \end{array} \right.$ cộng vế theo vế ta được:
$3\overrightarrow{AG}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}$
Mặt khác $\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$ (do G là trọng tâm tam giác BCD). Do vậy $\overrightarrow{AG}=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD}}{3}$
| Bài tập 2: Cho tứ diện ABCD. Lấy các điểm M và N lần lượt thuộc AD và BC sao cho $\overrightarrow{AM}=3\overrightarrow{MD}$, $\overrightarrow{NB}=-3\overrightarrow{NC}$. Biết $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{CD}=\overrightarrow{b}$.
a) Hãy biểu diễn vectơ $\overrightarrow{MN}$theo $\overrightarrow{a}$ và $\overrightarrow{b}$ b) Gọi P và Q lần lượt là trun điểm của AD và BC. Chứng minh rằng ba vectơ $\overrightarrow{MN}$, $\overrightarrow{DC}$, $\overrightarrow{PQ}$ đồng phẳng. c) Gọi G là trung điểm của PQ, chứng minh rằng G là trọng tâm tứ diện ABCD. |
Lời giải chi tiết
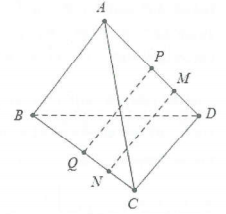
a) Ta có: $\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DC}+\overrightarrow{CN}\left( 1 \right)$
Lại có: $\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN}\left( 2 \right)$
Lấy $\left( 2 \right)+3.\left( 1 \right)$ ta được $4\overrightarrow{MN}=\overrightarrow{AB}+3\overrightarrow{DC}$
Do đó $\overrightarrow{MN}=\frac{1}{4}\overrightarrow{a}-\frac{3}{4}\overrightarrow{b}$
b) Ta có: $\left\{ \begin{array} {} \overrightarrow{MN}=\overrightarrow{MP}+\overrightarrow{PQ}+\overrightarrow{QN} \\ {} \overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{DC}+\overrightarrow{CN} \\ \end{array} \right.\Rightarrow 2\overrightarrow{MN}=\overrightarrow{PQ}+\overrightarrow{DC}$
Suy ra $\overrightarrow{MN}=\frac{1}{2}\left( \overrightarrow{PQ}+\overrightarrow{DC} \right)$$\Rightarrow $ba vectơ $\overrightarrow{MN}$, $\overrightarrow{DC}$, $\overrightarrow{PQ}$ đồng phẳng.
c) Theo tính chất trung điểm ta có: $\left\{ \begin{array} {} \overrightarrow{GA}+\overrightarrow{GD}=2\overrightarrow{GP} \\ {} \overrightarrow{GB}+\overrightarrow{GC}=2\overrightarrow{GQ} \\ \end{array} \right.\Rightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=2\left( \overrightarrow{GP}+\overrightarrow{GQ} \right)$
Mặt khác $\overrightarrow{GP}+\overrightarrow{GQ}=\overrightarrow{0}\Rightarrow \overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$$\Rightarrow $ G là trọng tâm tứ diện ABCD.
| Bài tập 3: Cho hình lăng trụ tam giác ABC.A’ B’C' có $\overrightarrow{AA'}=\overrightarrow{a}$, $\overrightarrow{AB}=\overrightarrow{b}$, $\overrightarrow{AC}=\overrightarrow{c}$
Gọi I và J lần lượt là trung điểm của BB' và A'C', điểm K thuộc B'C sao cho $\overrightarrow{KC'}=-2\overrightarrow{KB'}$ a) Hãy biểu thị vectơ $\overrightarrow{B'C}$; $\overrightarrow{CI}$ và $\overrightarrow{BJ}$ qua 3 vectơ $\overrightarrow{a}$, $\overrightarrow{b}$, $\overrightarrow{c}$ b) Biểu thị vectơ $\overrightarrow{AK}$ theo vectơ $\overrightarrow{AI}$ và $\overrightarrow{AJ}$ từ đó suy ra 3 vectơ $\overrightarrow{AK}$ ,$\overrightarrow{AI}$, $\overrightarrow{AJ}$ đồng phẳng. |
Lời giải chi tiết
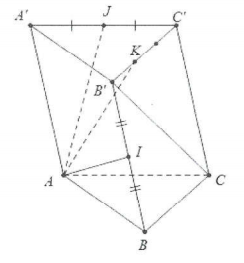
a) Ta có: $\overrightarrow{B'C}=\overrightarrow{B'C'}+\overrightarrow{B'B}$ (theo quy tắc hình bình hành)
Suy ra $\overrightarrow{B'C}=\overrightarrow{BC}+\overrightarrow{A'A}=\overrightarrow{AC}-\overrightarrow{AB}-\overrightarrow{AA'}=\overrightarrow{c}-\overrightarrow{b}-\overrightarrow{a}$
Lại có: $\overrightarrow{CI}=\overrightarrow{CB}+\overrightarrow{BI}=\left( \overrightarrow{AB}-\overrightarrow{AC} \right)+\frac{1}{2}\overrightarrow{BB'}=\overrightarrow{b}-\overrightarrow{c}+\frac{1}{2}\overrightarrow{a}$
Mặtkhác:
$\overrightarrow{BJ}=\overrightarrow{BA}+\overrightarrow{AA'}+\overrightarrow{A'J}=-\overrightarrow{AB}+\overrightarrow{A'C'}=-\overrightarrow{b}+\overrightarrow{a}+\frac{1}{2}\overrightarrow{AC}=-\overrightarrow{b}+\overrightarrow{a}+\frac{c}{2}$
b) Ta có: $\overrightarrow{AK}=\overrightarrow{AI}+\overrightarrow{IB'}+\overrightarrow{B'K}\left( 1 \right)$
$\overrightarrow{AK}=\overrightarrow{AJ}+\overrightarrow{JC'}+\overrightarrow{C'K}\left( 2 \right)$
Lấy $2.\left( 1 \right)+\left( 2 \right)$ ta được:
$3\overrightarrow{AK}=2\overrightarrow{AI}+\overrightarrow{AJ}+2\overrightarrow{IB'}+\overrightarrow{JC'}+\underbrace{2\overrightarrow{B'K}+\overrightarrow{C'K}}_{0}=2\overrightarrow{AI}+\overrightarrow{AJ}+\overrightarrow{BB'}+\overrightarrow{A'J}=2\overrightarrow{AI}+\overrightarrow{AJ}+\overrightarrow{AJ}$
Vậy $\overrightarrow{AK}=\frac{2}{3}\left( \overrightarrow{AI}+\overrightarrow{AJ} \right)$.
| Bài tập 4: Cho hình hộp ABCD.A'B'C'D'. Đặt $\overrightarrow{BA}=\overrightarrow{a}$, $\overrightarrow{BB'}=\overrightarrow{b}$, $\overrightarrow{BC}=\overrightarrow{c}$. Gọi M và N lần lượt là hai điểm nằm trên AC và DC’ sao cho MN//BD’. Tính tỷ số $\frac{MN}{BD'}$ |
Lời giải chi tiết
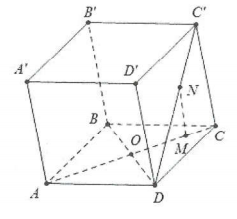
Giả sử: $\overrightarrow{MC}=n\overrightarrow{AC}$, $\overrightarrow{C'N}=m\overrightarrow{C'D}$
Ta có: $\overrightarrow{BD'}=\overrightarrow{BD}+\overrightarrow{DD'}=\overrightarrow{BA}+\overrightarrow{BC}+\overrightarrow{DD'}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}$
Lại có: $\overrightarrow{MN}=\overrightarrow{MC}+\overrightarrow{CC'}+\overrightarrow{C'N}=n\overrightarrow{AC}+\overrightarrow{b}+m\overrightarrow{C'D}$
$=n.\left( \overrightarrow{BC}-\overrightarrow{BA} \right)+\overrightarrow{b}+m\left( \overrightarrow{C'C}+\overline{CD} \right)$
$=n.\left( \overrightarrow{c}-\overrightarrow{a} \right)+\overrightarrow{b}+m\left( -\overrightarrow{b}+\overline{a} \right)=\left( m-n \right)\overrightarrow{a}+\left( 1-m \right)\overrightarrow{b}+n\overrightarrow{c}$
Khi đó $MN//BD'\Rightarrow \overrightarrow{MN}=k.\overrightarrow{BD'}$
$\frac{m-n}{1}=\frac{1-m}{1}=\frac{n}{1}=k\Leftrightarrow \left\{ \begin{array} {} m=\frac{2}{3} \\ {} n=\frac{1}{3} \\ \end{array} \right.\Rightarrow \frac{MN}{B'D'}=k=\frac{1}{3}$
| Bài tập 5: Cho hình hộp ABCD.A'B'C'D'. Gọi I là giao điểm của hai đường chéo của hình bình hành ABB'A' và K là giao điểm của hai đường chéo của hình bình hành BCC'A. Biểu thị vectơ $\overrightarrow{BD}$ theo 2 vectơ $\overrightarrow{IK}$ và $\overrightarrow{C'B'}$ từ đó suy ra ba vectơ $\overrightarrow{BD}$, $\overrightarrow{IK}$, $\overrightarrow{C'B'}$ đồng phẳng. |
Lời giải chi tiết
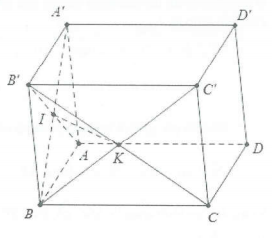
Ta có: $\overrightarrow{BD}=\overrightarrow{BC}+\overrightarrow{CD}=-\overrightarrow{C'B}+\left( \overrightarrow{AD}-\overrightarrow{AC} \right)$
$=-\overrightarrow{C'B'}+\overrightarrow{B'C'}-2\overrightarrow{IK}$ (vì $\overrightarrow{AC}=2\overrightarrow{IK}$)
Suy ra $\overrightarrow{BD}=-2\overrightarrow{C'B'}-2\overrightarrow{IK}$
Do đó ba vectơ $\overrightarrow{BD}$, $\overrightarrow{IK}$, $\overrightarrow{C'B'}$ đồng phẳng.
| Bài tập 6: Trong không gian cho tam giác ABC. Chứng minh rằng nếu có một điểm O trong không gian sao cho $\overrightarrow{OM}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$, đồng thời , $x+y+z=1$ thì điểm M thuộc mặt phẳng $\left( ABC \right)$. |
Lời giải chi tiết
Ta có: $\overrightarrow{OM}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}\Leftrightarrow \left( x+y+z \right)\overrightarrow{OM}=x\overrightarrow{OA}+y\overrightarrow{OB}+z\overrightarrow{OC}$
$\Leftrightarrow x\overrightarrow{MA}+y\overrightarrow{MB}+z\overrightarrow{MC}=\overrightarrow{0}$
Nếu $x=0\Rightarrow \Leftrightarrow y\overrightarrow{MB}+z\overrightarrow{MC}=\overrightarrow{0}$$\Rightarrow $ M, B, C thẳng hàng nên A, B, C, M đồng phẳng
Nếu $x\ne 0\Rightarrow \overrightarrow{MA}=\frac{-y}{x}\overrightarrow{MB}-\frac{z}{x}\overrightarrow{MC}$$\Rightarrow $ A, B, C, M đồng phẳng.
| Bài tập 7: Cho tứ diện ABCD. Gọi P và P lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AB và CD lần lượt lấy các điểm M, N sao cho $\frac{AM}{AC}=\frac{BN}{BD}=k\left( k>0 \right)$. Chứng minh rằng 3 vectơ $\overrightarrow{PQ}$, $\overrightarrow{PM}$, $\overrightarrow{PN}$ đồng phẳng |
Lời giải chi tiết
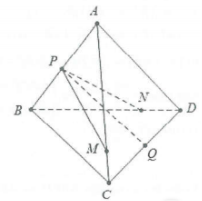
Ta có: $\overrightarrow{PQ}=\frac{1}{2}\left( \overrightarrow{PC}+\overrightarrow{PD} \right)=\frac{1}{2}\left[ \left( \overrightarrow{AC}-\overrightarrow{AP} \right)+\left( \overrightarrow{BD}-\overrightarrow{BP} \right) \right]$
$=\frac{1}{2}\left[ \overrightarrow{AC}+\overrightarrow{BD}-\left( \overrightarrow{AP}+\overrightarrow{BP} \right) \right]=\frac{1}{2}\frac{\overrightarrow{AM}+\overrightarrow{BN}}{k}$
Lại có: $\left\{ \begin{array} {} \overrightarrow{AM}=\overrightarrow{AP}+\overrightarrow{PM} \\ {} \overrightarrow{BN}=\overrightarrow{BP}+\overrightarrow{PN} \\ \end{array} \right.$ nên $\overrightarrow{PQ}=\frac{1}{2k}\left( \overrightarrow{PM}+\overrightarrow{PN} \right)$
(Do $\overrightarrow{AP}+\overrightarrow{BP}=\overrightarrow{0}$)
Do đó $\overrightarrow{PQ}=\frac{1}{2k}\left( \overrightarrow{PM}+\overrightarrow{PN} \right)$$\Rightarrow $ M, N, P, Q đồng phẳng
TOÁN LỚP 12
