Cách xác định nhanh Góc giữa đường thẳng và mặt phẳng – Công thức và bài tập có đáp án chi tiết

Cách xác định nhanh Góc giữa đường thẳng và mặt phẳng – Công thức và bài tập có đáp án

■ Định nghĩa:

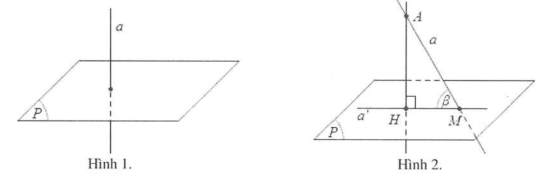
Nếu đường thẳng a vuông góc với mặt phẳng (P) thì ta nói rằng góc giữa đường thẳng a và mặt phẳng (P) bằng $90{}^\circ$ (hình 1).

Nếu đường thẳng a không vuông góc với mặt phẳng (P) thì góc giữa a và hình chiếu ${a}'$ của nó trên (P) được gọi là góc giữa đường thẳng a và mặt phẳng (P) (hình 2).

Chú ý: Góc giữa đường thẳng và mặt phẳng không vượt quá $90{}^\circ$.

■ Phương pháp giải:

Sử dụng định nghĩa góc giữa đường thẳng và mặt phẳng.

Cách tìm hình chiếu ${a}'$ của a trên mặt phẳng (P) ta có thể làm như sau:

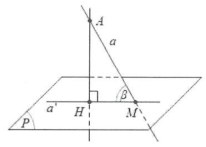
Tìm giao điểm $M=a\cap \left( P \right).$

Tìm một điểm A tùy ý trên đường thẳng a $\left( A\ne M \right)$ và xác định hình chiếu vuông góc H của A trên mặt phẳng (P). Khi đó, ${a}'$ là đường thẳng đi qua hai điểm A và M. Ta có: $\beta =\widehat{\left( a;\left( P \right) \right)}=\widehat{AMH}.$

Xét tam giác vuông AMH ta có: $\left\{ \begin{array}  {} \cos \beta =\frac{HM}{AM} \\  {} \tan \beta =\frac{AH}{MH} \\  {} \sin \beta =\frac{AH}{AM}=\frac{d\left( A;\left( P \right) \right)}{AM} \\ \end{array} \right.$ (trong đó $d\left( A;\left( P \right) \right)$ là khoảng cách từ điểm A đến mặt phẳng (P)).