Cách Viết phương trình đường thẳng cắt d1 và d2 đồng thời song song với d (hoặc vuông góc với (P), hoặc đi qua điểm M).

Cách Viết phương trình đường thẳng ∆ cắt d₁ và d₂ đồng thời song song với d (hoặc vuông góc với (P), hoặc đi qua điểm M). 

Phương pháp viết phương trình đường thẳng song song với đường thẳng d và cắt hai đường thẳng d1 và d2

Giả sử ∆ cắt d₁ và d₂ lần lượt tại A và B, ta tham số hóa 2 điểm $A\in {{d}_{1}};B\in {{d}_{2}}$theo ẩn t và u.

Do $\Delta //d\Rightarrow \overrightarrow{{{u}_{\Delta }}}=k.\overrightarrow{{{u}_{d}}}\Leftrightarrow \overrightarrow{AB}=k.\overrightarrow{{{u}_{d}}}\Rightarrow t;u\Rightarrow $tọa độ các điểm A,B.

Phương trình đường thẳng cần tìm là AB.

Chú ý:

R Trường hợp: $\Delta \bot (P)\Rightarrow \overrightarrow{AB}=k.\overrightarrow{{{n}_{(P)}}}\Rightarrow $t và u.

R Trường hợp: ∆ đi qua điểm M $\Rightarrow M,A,B$thẳng hàng ta giải $\overrightarrow{MA}=k.\overrightarrow{MB}\Rightarrow t;u$và k.

Bài tập viết phương trình đường thẳng oxyz có đáp án chi tiết

Lời giải chi tiết

Lấy $M\in {{d}_{1}}\Rightarrow M(1+2t;-1-t;t);N\in {{d}_{2}}\Rightarrow N(-1+u;-1;-u)$

Suy ra $\overrightarrow{MN}=\left( u-2t-2;t;-u-t \right)$

Do $d\bot (P)\Rightarrow \overrightarrow{MN}=k.\overrightarrow{{{n}_{(P)}}}\Rightarrow \frac{u-2t-2}{1}=\frac{t}{1}=\frac{-u-t}{1}\Leftrightarrow \left\{ \begin{array}  {} u=\frac{4}{5} \\  {} t=-\frac{2}{5} \\ \end{array} \right.\Rightarrow M\left( \frac{1}{5};\frac{-3}{5};\frac{-2}{5} \right)$

Phương trình đường thẳng d là: ${{d}_{1}}:\frac{x-\frac{1}{5}}{1}=\frac{y+\frac{3}{5}}{1}=\frac{z+\frac{2}{5}}{1}$

Lời giải chi tiết

Gọi $B(1+2u;-3-u;-1+2u)\in {{d}_{1}}$và $C(2-t;t;3t)\in {{d}_{2}}$

Ta có: $\overrightarrow{AB}=\left( 2u;u-2;2u-2 \right);\overrightarrow{AC}=(1-t;t+1;3t-1)$

Do A, B, C thẳng hàng nên $\overrightarrow{AB}=k.\overrightarrow{AC}\Rightarrow \left\{ \begin{array}  {} 2u=k(1-t) \\  {} u-2=k(t+1) \\  {} 2u-2=k(3t-1) \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} 2u-k+kt=0 \\  {} u-k-kt=2 \\  {} 2u+k-3kt=2 \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} u=0 \\  {} k=-1 \\  {} kt=-1 \\ \end{array} \right.$

Suy ra $u=0;t=1\Rightarrow \overrightarrow{{{u}_{d}}}=(0;1;1)\Rightarrow d:\left\{ \begin{array}  {} x=1 \\  {} y=-1+t \\  {} z=1+t \\ \end{array} \right.$

Lời giải chi tiết

Giả sử đường thẳng d cắt d₁, d₂ lần lượt tại

$M,N\Rightarrow M(1-{{t}_{1}};3-2{{t}_{1}};-2+{{t}_{1}}),N(5-3{{t}_{2}};-1+2{{t}_{2}};2+{{t}_{2}})$

Ta có $\overrightarrow{MN}=\left( {{t}_{1}}-3{{t}_{2}}+2;2{{t}_{1}}+2{{t}_{2}}-4;-{{t}_{1}}+{{t}_{2}}+4 \right)$và $\overrightarrow{{{n}_{P}}}=\left( 1;2;3 \right)$

Mà d vuông góc với (P) nên $\overrightarrow{MN}=k.\overrightarrow{{{n}_{P}}}\Rightarrow \left\{ \begin{array}  {} {{t}_{1}}-3{{t}_{2}}+2=k \\  {} 2{{t}_{1}}+2{{t}_{2}}-4=2k \\  {} -{{t}_{1}}+{{t}_{2}}+4=3k \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} {{t}_{1}}=2 \\  {} {{t}_{2}}=1 \\  {} k=1 \\ \end{array} \right.\Rightarrow \left\{ \begin{array}  {} M(1;-1;0) \\  {} N(2;1;3) \\ \end{array} \right.$

$\overrightarrow{MN}=(1;2;3)\Rightarrow d:\frac{x-1}{1}=\frac{y+1}{2}=\frac{z}{3}$. Chọn A.

Lời giải chi tiết

Gọi $A(-1+2t;-1+t;2-t)\in {{d}_{1}};B(1-u;2+u;3+3u)\in {{d}_{2}}$

Khi đó: $\overrightarrow{AB}=\left( 2-u-2t;3+u-t;1+3u+t \right)$

Do $AB//d\Rightarrow d:\frac{2-u-2t}{1}=\frac{3+u-t}{1}=\frac{1+3u+t}{-1}\Leftrightarrow \left\{ \begin{array}  {} t=1 \\  {} u=-1 \\ \end{array} \right.\Rightarrow A(1;0;1)\Rightarrow (\Delta ):\frac{x-1}{1}=\frac{y}{1}=\frac{z-1}{-1}$

Chọn B.

Lời giải chi tiết

Giả sử $d\cap {{d}_{1}}=A\Rightarrow A\in {{d}_{1}}$nên $A(2u;1-u;u-2)$

$d\cap {{d}_{2}}=B\Rightarrow B\in {{d}_{2}}$nên $B(2t-1;t+1;3)$

Vì thế $\overrightarrow{AB}=\left( 2t-2u-1;t+u;5-u \right)$là vecto chỉ phương của d.

Do $d\bot (P)$nên $\overrightarrow{AB}//\overrightarrow{n}=(7;1;-4)$ở đây $\overrightarrow{n}$là vecto pháp tuyến của mp (P)

Từ đó có hệ phương trình $\frac{2t-2u-1}{7}=\frac{t+u}{1}=\frac{5-u}{-4}\Leftrightarrow \left\{ \begin{array}  {} 2t-2u-1=7t+7u \\  {} 4(t+u)=u-5 \\ \end{array} \right.$

$\Leftrightarrow \left\{ \begin{array}  {} t=-2 \\  {} u=1 \\ \end{array} \right.\Rightarrow \overrightarrow{AB}=(-7;-1;4)$và đường thẳng d đi qua điểm $A(2;0;-1)$nên

$(d):\frac{x-2}{7}=\frac{y}{1}=\frac{z+1}{-4}$. Chọn B.

Lời giải chi tiết

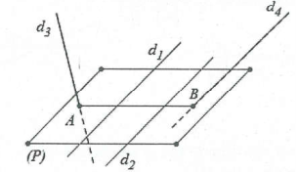
Ta có $\overrightarrow{{{u}_{({{d}_{1}})}}}=\left( 1;2;-2 \right)$và $\overrightarrow{{{u}_{({{d}_{2}})}}}=\left( 2;4;-4 \right)$suy ra $\overrightarrow{{{u}_{({{d}_{2}})}}}=2\overrightarrow{{{u}_{({{d}_{1}})}}}\Rightarrow ({{d}_{1}})//({{d}_{2}})$

Phương trình mặt phẳng (P) chứa (d₁), d(₂) là $y+z-2=0$

Gọi $A=({{d}_{3}})\cap (P)\Rightarrow A\left( 1;\frac{1}{2};\frac{3}{2} \right)$và $B=({{d}_{4}})\cap (P)\Rightarrow B\left( 4;2;0 \right)\to \overrightarrow{AB}=\left( 3;\frac{3}{2};-\frac{3}{2} \right)$

Khi đó $\overrightarrow{AB}$ và ${{u}_{({{d}_{1}})}}$không cùng phương $\Rightarrow AB$cắt đường thẳng (d₁), (d₂)

Vậy $\overrightarrow{{{u}_{(\Delta )}}}=\frac{2}{3}\overrightarrow{AB}=\left( 2;1;-1 \right)$là vecto chỉ phương của đường thẳng cắt (d₁), (d₂), (d₃), (d₄).

Chọn B.

Lời giải chi tiết

Gọi $A(1+t;2+3t;t)\in {{d}_{1}};B(-1-u;1+2u;2+4u)\in {{d}_{2}}$

Ta có: $\overrightarrow{MA}=k.\overrightarrow{MB}\Rightarrow \left\{ \begin{array}  {} t-2=k(-u-4) \\  {} 3t-1=k(2u-2) \\  {} t+2=k(4u+4) \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}  {} t+4k+ku=2 \\  {} 3t+2k-2ku=1 \\  {} t-4k-4ku=-2 \\ \end{array} \right.$

Giải hệ với ẩn t; k và ku $\Rightarrow \left\{ \begin{array}  {} t=0 \\  {} k=\frac{1}{2} \\  {} ku=0 \\ \end{array} \right.\Rightarrow t=0;u=0\Rightarrow A(1;2;0);B(-1;1;2)\Rightarrow AB=3$. Chọn A.