Cách tính nhanh Góc giữa hai mặt bên có đáp án chi tiết

Tính nhanh Góc giữa hai mặt bên có đáp án chi tiết
Phương pháp xác định góc giữa hai mặt bên:
Tính góc giữa hai mặt bên (SAC) và (SBC).
þ Cách 1: Tính góc giữa 2 đường thẳng a và b lần lượt vuông góc với mặt phẳng (SAC) và (SBC).
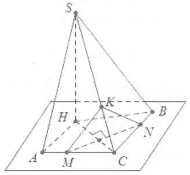
þ Cách 2: Dựng đường cao $SH\bot \left( ABC \right).$
Lấy điểm M bất kỳ thuộc AC, dựng $MN\bot HC.$
Lại có: $MN\bot SH\Rightarrow MN\bot \left( SHC \right)\Rightarrow MN\bot SC.$
Dựng $MK\bot SC\Rightarrow SC\bot \left( MKN \right)$
$\Rightarrow \widehat{\left( \left( SAC \right);\left( SBC \right) \right)}=\widehat{\left( MK,KN \right)}.$
Bài tập tính nhanh góc giữa hai mặt bên có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), đáy ABC tam giác vuông tại B có $AB=a,BC=a\sqrt{3}$. Biết $SA=\frac{a\sqrt{6}}{2}$, tính góc giữa hai mặt phẳng (SAC) và (SBC). |
Lời giải chi tiết
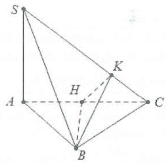
Dựng $BH\bot AC\Rightarrow BH\bot \left( SAC \right)\Rightarrow BH\bot SC.$
Dựng $BH\bot SC\Rightarrow \left( HKB \right)\bot SC$
$\Rightarrow \widehat{\left( \left( SBC \right);\left( SAC \right) \right)}=\widehat{HKB}.$
Ta có: $SA=\sqrt{S{{B}^{2}}-A{{B}^{2}}}=\frac{a\sqrt{2}}{2};AC=\sqrt{A{{B}^{2}}-B{{C}^{2}}}=2a.$
Khi đó $\sin \widehat{KCH}=\frac{HK}{HC}=\frac{SA}{SC}=\frac{SA}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{1}{3}\Rightarrow HK=\frac{a}{3}.$
Mặt khác: $BH=\frac{BA.BC}{AC}=\frac{a\sqrt{3}}{2}\Rightarrow \tan \widehat{HKB}=\frac{BH}{HK}=\sqrt{3}$
$\Rightarrow \widehat{HKB}=60{}^\circ .$ Vậy góc giữa hai mặt phẳng (SAC) và (SBC) bằng $60{}^\circ $.
| Bài tập 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a có $\widehat{ABC}=60{}^\circ $, $SA\bot \left( ABC \right)$ và $SA=a$. Tính cosin góc giữa:
a) (SBC) và (SCD). b) (SBC) và (SCD). |
Lời giải chi tiết
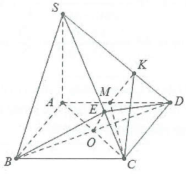
a) Nhận xét $\Delta ABC$ là tam giác đều cạnh a vì $AB=BC=a$ và $\widehat{ABC}=60{}^\circ $. Gọi O là tâm của hình thoi ABCD.
Ta có: $\left\{ \begin{array} {} BD\bot AC \\ {} BD\bot SA \\ \end{array} \right.\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot SC.$
Dựng $BE\bot SC\Rightarrow SC\bot \left( BED \right).$
Mặt khác: $SA=AC=a\Rightarrow \Delta SAC$ vuông cân tại A suy ra
$\widehat{ECO}=45{}^\circ $. Khi đó $OE=OC\sin 45{}^\circ =\frac{a\sqrt{2}}{4}.$
Lại có: $OB=\frac{a\sqrt{3}}{2}\Rightarrow \tan \widehat{BEO}=\frac{OB}{OE}=\sqrt{6}.$
Do $\widehat{BED}=2\widehat{BEO}$ sử dụng công thức lượng giác hoặc máy tính CASIO ta tính được $\cos \widehat{BED}=\frac{-5}{7}$.
Cách khác: Ta có: $BE=DE=\sqrt{O{{E}^{2}}+O{{B}^{2}}}=\frac{\sqrt{14}}{4}\Rightarrow \cos \widehat{BED}=\frac{E{{B}^{2}}+E{{D}^{2}}-B{{D}^{2}}}{2.EB.ED}=\frac{-5}{7}.$
Suy ra $\widehat{\left( \left( SBC \right);\left( SCD \right) \right)}=\frac{5}{7}.$
b) Dựng $CM\bot AD$ ta có: $\left\{ \begin{array} {} CM\bot AD \\ {} CM\bot SA \\ \end{array} \right.\Rightarrow CM\bot \left( SAD \right)\Rightarrow CM\bot SD.$
Dựng $CK\bot SD\Rightarrow SD\bot \left( MKC \right).$
Tam giác ACD đều cạnh a nên $CM=\frac{a\sqrt{3}}{2}$. Do $SA=AD=a\Rightarrow \Delta SAD$ vuông cân tại A suy ra $\widehat{SDM}=45{}^\circ $. Do đó $MK=MD\sin 45{}^\circ =\frac{a\sqrt{2}}{4}.$
Suy ra $\tan \widehat{MKC}=\frac{CM}{MK}=\sqrt{6}\Rightarrow \cos \widehat{MKC}=\frac{1}{\sqrt{7}}.$
Vậy $\cos \widehat{\left( \left( SCD \right);\left( SAD \right) \right)}=\frac{1}{\sqrt{7}}.$
| Bài tập 3: Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều cạnh a với $AD=2a$, biết rằng $SA\bot \left( ABCD \right)$ và mặt phẳng (SCD) tạo với đáy một góc $45{}^\circ $. Tính cosin góc giữa 2 mặt phẳng (SCD) và (SBC). |
Lời giải chi tiết
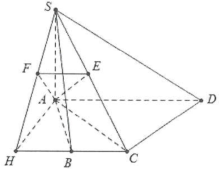
Do $AD=2a$ nên tứ giác ABCD nội tiếp trong đường tròn đường kính $AD=2a$
Ta có: $\left\{ \begin{array} {} AC\bot CD \\ {} CD\bot SA \\ \end{array} \right.\Rightarrow CD\bot \left( SAC \right)$
Suy ra $\widehat{\left( \left( SCD \right);\left( ABCD \right) \right)}=\widehat{SCA}=45{}^\circ $
$\Rightarrow SA=AC=\sqrt{4{{a}^{2}}-{{a}^{2}}}=a\sqrt{3}$
Dựng $AE\bot SC\Rightarrow AE\bot \left( SCD \right)$
Dựng $\left\{ \begin{array} {} AH\bot BC \\ {} AF\bot SH \\ \end{array} \right.\Rightarrow AF\bot \left( SBC \right)$, góc giữa 2 mặt phẳng (SCD) và (SBC) là góc giữa AE và AF.
Tacó: $AE=\frac{SA.AC}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{a\sqrt{6}}{2}$; $AH=AC\sin 30{}^\circ =\frac{a\sqrt{3}}{2}.$
Suy ra $AF=\frac{SA.AH}{\sqrt{S{{A}^{2}}+A{{H}^{2}}}}=\frac{a\sqrt{3}}{\sqrt{5}}$, do $AF\bot \left( SBC \right)\Rightarrow AF\bot FE$. Do đó $\cos \widehat{FAE}=\frac{AF}{AE}=\frac{\sqrt{10}}{5}.$
| Bài tập 4: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với $AB=a;AD=a\sqrt{3}$, cạnh bên $SA\bot \left( ABCD \right)$. Biết mặt phẳng (SBC) tạo với mặt đáy một góc $60{}^\circ $. Tính cosin góc giữa hai mặt phẳng (SBC) và (SCD). |
Lời giải chi tiết
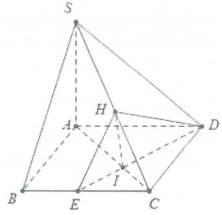
Do $SA\bot \left( ABCD \right)$ và $BC\bot AB\Rightarrow BC\bot \left( SBA \right)$
Do đó $\widehat{\left( \left( SBC \right);\left( ABC \right) \right)}=\widehat{SBA}=60{}^\circ ;AC=2a$
$\Rightarrow SA=AB\sin 60{}^\circ =a\sqrt{3}.$
Dựng $DE\bot AC$$\left( E\in BC \right)$ tại I, mặt khác $DE\bot SA\Rightarrow DE\bot \left( SAC \right)\Rightarrow DE\bot SC$. Dựng $IH\bot SC$
$\Rightarrow SC\bot \left( EHD \right)$. Ta có: $DI=DC\sin \widehat{ICD}$ trong đó $\tan \widehat{ICD}=\sqrt{3}\Rightarrow \widehat{ICD}=60{}^\circ .$
Suy ra $DI=a\sin 60{}^\circ =\frac{a\sqrt{3}}{2};DE=\frac{D{{C}^{2}}}{DI}=\frac{2a}{\sqrt{3}}.$
$\Rightarrow IE=DE-DI=\frac{a\sqrt{3}}{6}\Rightarrow CI=\sqrt{EI.DI}=\frac{a}{2};\sin \widehat{ICH}=\frac{SA}{SC}=\frac{\sqrt{3}}{\sqrt{7}}\Rightarrow IH=IC\sin \widehat{IHC}=\frac{a\sqrt{3}}{2\sqrt{7}}$
Suy ra $EH=\sqrt{E{{I}^{2}}+I{{H}^{2}}}=\frac{2a}{\sqrt{21}};ED=\frac{a\sqrt{42}}{7}.$
Do đó $\cos \widehat{EHD}=\frac{E{{H}^{2}}+H{{D}^{2}}-E{{D}^{2}}}{2.EH.HD}=\frac{-\sqrt{2}}{4}<0\Rightarrow \cos \widehat{\left( \left( SBC \right);\left( SCD \right) \right)}=\frac{\sqrt{2}}{4}.$
| Bài tập 5: Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh a. Biết $SA\bot \left( ABCD \right)$, tính độ dài đoạn thẳng SA để góc giữa mặt phẳng (SBC) và (SCD) bằng $60{}^\circ $. |
Lời giải chi tiết
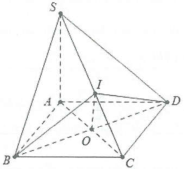
Ta có: $\left\{ \begin{array} {} BD\bot AC \\ {} BD\bot SA \\ \end{array} \right.\Rightarrow BD\bot \left( SAC \right)\Rightarrow BD\bot SC.$
Kẻ $BI\bot SC\Rightarrow SC\bot \left( BID \right).$
Vậy $\widehat{\left( \left( SBC \right);\left( SCD \right) \right)}=\widehat{\left( BI;ID \right)}=60{}^\circ .$
Dễ thấy $\left\{ \begin{array} {} OI\bot SC \\ {} \widehat{BIO}=\frac{1}{2}\widehat{BID} \\ \end{array} \right..$
■ Trường hợp 1: $\widehat{BID}=60{}^\circ \Rightarrow \widehat{BIO}=30{}^\circ .$
Ta có: $\tan \widehat{BIO}=\frac{BO}{IO}=\tan 30{}^\circ \Rightarrow OI=\frac{a\sqrt{6}}{2}>OC=\frac{a\sqrt{2}}{2}$ (vô lý).
(OI là cạnh góc vuông, OC là cạnh huyền của tam giác vuông OIC).
■ Trường hợp 2: $\widehat{BID}=120{}^\circ \Rightarrow \widehat{BIO}=60{}^\circ .$
Ta có: $\tan \widehat{BIO}=\frac{BO}{IO}=\tan 60{}^\circ \Rightarrow OI=\frac{a\sqrt{6}}{6}.$
Mặt khác: $\sin \widehat{ICO}=\frac{OI}{OC}=\frac{\sqrt{3}}{3}\Rightarrow \tan \widehat{ICO}=\frac{1}{\sqrt{2}}\Rightarrow SA=AC\tan \widehat{ICO}=a.$
| Bài tập 6: Cho hình chóp S.ABCD có đáy ABCD là nửa lục giác đều cạnh a với $AB=2a$, biết rằng $SA\bot \left( ABCD \right)$ và $SA=a\sqrt{3}$. Tính tan góc giữa 2 mặt phẳng (SAB) và (SCD). |
Lời giải chi tiết
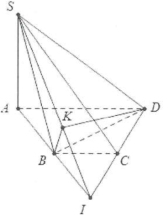
Do ABCD là nửa lục giác đều cạnh a với $AB=2a\Rightarrow $ABCD nội tiếp đường tròn đường kính AB. Do đó $\widehat{ABD}=90{}^\circ .$
Gọi $I=AB\cap CD\Rightarrow SI=\left( SAB \right)\cap \left( SCD \right).$
Do $\left\{ \begin{array} {} AI\bot BD \\ {} BD\bot SA \\ \end{array} \right.\Rightarrow BD\bot \left( SAI \right)\Rightarrow BD\bot SI.$
Dựng $BK\bot SI\Rightarrow SI\bot \left( BKD \right).$
Khi đó $\widehat{\left( \left( SAB \right);\left( SCD \right) \right)}=\widehat{\left( BK;KD \right)}=\widehat{BKD}.$
Do $BD\bot \left( SAI \right)\Rightarrow BD\bot BK\Rightarrow \Delta KBD$ vuông tại B có $BD=\sqrt{A{{D}^{2}}-A{{B}^{2}}}=a\sqrt{3}.$
Do $\left\{ \begin{array} {} BC//AD \\ {} BC=\frac{1}{2}AD \\ \end{array} \right.\Rightarrow $ BC là đường trung bình trong tam giác $AID\Rightarrow AB=BI$ và $AI=2a$
$\Rightarrow BK=\frac{1}{2}d\left( A;SI \right)=\frac{1}{2}.\frac{SA.AI}{\sqrt{S{{A}^{2}}+A{{I}^{2}}}}=\frac{a\sqrt{21}}{7}\Rightarrow \tan \widehat{BKD}=\frac{BD}{BK}=\sqrt{7}.$
TOÁN LỚP 12