Cách tính khoảng cách giữa hai đường thẳng chéo nhau

Cách tính khoảng cách giữa hai đường thẳng chéo nhau
Đường vuông góc chung và đoạn vuông góc chung hai đường chéo nhau.
- Đường thẳng $\Delta $ cắt hai đường thẳng chéo nhau a, b và cùng vuông góc với mỗi đường thẳng ấy được gọi là đường vuông góc chung của a và b.
- Đường thẳng vuông góc chung $\Delta $ cắt hai đường thẳng chéo nhau a và b lần lượt tại M và N thì độ dài đoạn thẳng MN gọi là khoảng cách giữa hai đường thẳng chéo nhau a và b.
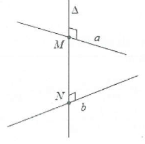
Cách xác định đoạn vuông góc chung của 2 đường chéo nhau.
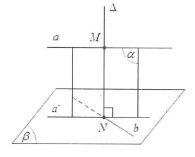
Cho 2 đường thẳng chéo nhau a và b. Gọi $\left( \beta \right)$ là mặt phẳng chứa b và song song với a, a’ là hình chiếu vuông góc của a trên $\Rightarrow CD\bot (SHC)\Rightarrow \overset\frown{SCH}={{60}^{\circ }}$.
Vì $a//\left( \beta \right)$ nên $a//a'$. Gọi $N=a'\cap b$ và $\left( \alpha \right)$ là mặt phẳng chứa a và a’. Dựng đường thẳng $\Delta $ qua N và vuông góc chung và MN là đoạn vuông góc chung của a và b.
Nhận xét:
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại
- Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song với nó và chứa đường thẳng còn lại.
Phương pháp Khoảng cách giữa hai đường thẳng chéo nhau và vuông góc với nhau.
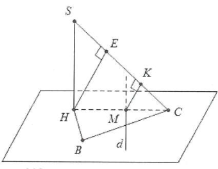
Phương pháp giải: Dựng đường vuông góc chung. Khảo sát khối chóp đỉnh S có đường cao SH, yêu cầu tính khoảng cách giữa 2 đường chéo nhau d (thuộc mặt đáy) và đường thẳng SC thuộc bên khối chóp trong trường hợp $d\bot SC$.
Dựng hình: Hình chiếu vuông góc của SC trên mặt phẳng đáy là HC
Mặt khác: $\left\{ \begin{array} {} SC\bot d \\ {} SH\bot d \\ \end{array} \right.\Rightarrow d\bot \left( SHC \right)$
Gọi $M=d\cap HC$, dựng $MK\bot SC$ khi đó MK là đoạn vuông góc chung của AC và SC
Cách tính: Dựng $HE\bot SC$ khi đó $\frac{MK}{HE}=\frac{MC}{HC}\Rightarrow MK=\frac{MC}{HC}.HE$
Xét tam giác vuông SHC ta có: $\frac{1}{H{{E}^{2}}}=\frac{1}{S{{H}^{2}}}+\frac{1}{H{{C}^{2}}}\Rightarrow HE=MK=d\left( d;SC \right)$
Bài tập tính khoảng cách giữa 2 đường thăng vuông góc với nhau và chéo nhau
| Bài tập 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a và $SA\bot (ABCD)$. Biết rằng SC tạo với mặt đáy một góc $60{}^\circ $
a) Tính khoảng cách giữa 2 đường thẳng AB và SD b) Tính khoảng cách giữa BD và SC. |
Lời giải chi tiết
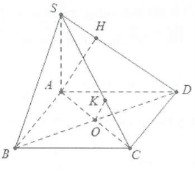
a) Ta có: $AC=a\sqrt{2}$. Do $SA\bot \left( ABCD \right)$ và SC tạo với đáy góc $60{}^\circ $ nên $\widehat{SCA}=60{}^\circ $
Khi đó $SA=AC\tan 60{}^\circ =a\sqrt{6}$
Do $\left\{ \begin{array} {} AB\bot AD \\ {} AB\bot SA \\ \end{array} \right.\Rightarrow AB\bot (SAD)$
Dựng $AH\bot SD$ suy ra AH là đoạn vuông góc chung của AB và SD
Ta có: $\frac{SA.AB}{\sqrt{S{{A}^{2}}+A{{B}^{2}}}}=\frac{a\sqrt{42}}{7}$
b) Ta có: $BD\bot SC$ tại O và $BD\bot SA$$\Rightarrow BD\bot \left( SAC \right)$
Dựng $OK\bot SC$$\Rightarrow OK\bot BD$ nên OK là đoạn vuông góc chung của BD và SC
Do đó $d\left( BD;SC \right)=OK=OC\sin \widehat{OCK}=\frac{a\sqrt{2}}{2}\sin 60{}^\circ =\frac{a\sqrt{6}}{4}$
| Bài tập 2: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, gọi I là trung điểm của AB. Hình chiếu vuông góc của S trên mặt đáy là trung điểm CI. Biết chiều cao của khối chóp là $h=a\sqrt{3}$. Tính khoảng cách d giữa đường thẳng AB và SC. |
Lời giải chi tiết
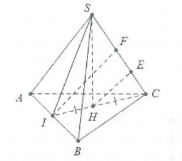
a) Ta có: $\left\{ \begin{array} {} CI\bot AB \\ {} SH\bot AB \\ \end{array} \right.\Rightarrow AB\bot (SIC)$
Dựng $IF\bot SC$ khi đó IF là đoạn vuông góc chung của AB và SC. Dựng $HE\bot SC$ ta có: $HE=\frac{1}{2}IF$
Lại có $CI=\frac{a\sqrt{3}}{2}\Rightarrow CH=\frac{a\sqrt{3}}{4}$
Khi đó $HE=\frac{SH.HC}{\sqrt{S{{H}^{2}}+H{{C}^{2}}}}=\frac{a\sqrt{51}}{17}\Rightarrow IF=\frac{2a\sqrt{51}}{17}$
| Bài tập 3: Cho hình chóp S.ABCD có đáy là hình thang vuông ABCD cạnh a và $SA\bot \left( ABCD \right)$. Biết mặt phẳng $\left( SBC \right)$ tạo với đáy một góc $60{}^\circ $
a) Tính khoảng cách giữa 2 đường thẳng SB và CD. b) Tính khoảng cách giữa 2 đường thẳng BD và SC. |
Lời giải chi tiết
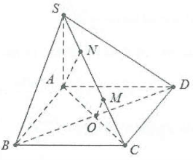
a) Do:$\left\{ \begin{array} {} BC\bot AB \\ {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAB)\Rightarrow BC\bot SB\Rightarrow BC$ là đoạn vuông góc chung của SB và CD.
Ta có: $d\left( SB;CD \right)=BC=a$
c) Mặt khác $BC\bot \left( SAB \right)$
Do đó $\widehat{\left( \left( SBC \right);\left( ABCD \right) \right)}=\widehat{SBA}=60{}^\circ $
Suy ra $SA=AB\tan 60{}^\circ =a\sqrt{3}$
Gọi O là tâm hình vuông ABCD ta có $\left\{ \begin{array} {} BD\bot AC \\ {} BD\bot SA \\ \end{array} \right.\Rightarrow BD\bot (SAC)$
Dựng $OM\bot SC$ khi đó OM là đường vuông góc chung của BD và SC
Ta có $\Delta CAS\sim \Delta CMO\left( g-g \right)\Rightarrow \frac{SC}{CO}=\frac{SA}{MO}\Rightarrow OM=\frac{SA.OC}{SC}=\frac{a\sqrt{3}.\frac{a\sqrt{2}}{2}}{\sqrt{S{{A}^{2}}+A{{C}^{2}}}}=\frac{a\sqrt{6}}{2\sqrt{5}}=\frac{a\sqrt{30}}{10}$
Cách 2: Dựng $AN\bot SC\Rightarrow OM=\frac{1}{2}AN$. Mặt khác $\frac{1}{A{{N}^{2}}}=\frac{1}{S{{A}^{2}}}+\frac{1}{A{{C}^{2}}}\Rightarrow AN=\frac{a\sqrt{30}}{5}$
Khi đó $d=OM=\frac{1}{2}AN=\frac{a\sqrt{30}}{10}$
| Bài tập 4: Cho chóp S.ABC có đáy ABC là tam giác vuông cân tại A, tam giác SBC là tam giác đều cạnh a và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách d giữa 2 đường thẳng SA và BC. |
Lời giải chi tiết
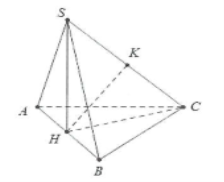
Gọi H là trung điểm của BC khi đó $SH\bot BC$
Mặt khác $(SBC)\bot (ABC)$ do đó $SH\bot (ABC)$
Ta có: $SH=\frac{a\sqrt{3}}{2}$ và $AB=AC=\frac{a}{\sqrt{2}};AH=\frac{BC}{2}=\frac{a}{2}$
Do $\left\{ \begin{array} {} BC\bot AH \\ {} BC\bot SH \\ \end{array} \right.\Rightarrow BC\bot (SHA)$. Dựng $HK\bot SA$ khi đó
HK là đoạn vuông góc chung của BC và SA.
Lại có: $HK=\frac{SH.AH}{\sqrt{S{{H}^{2}}+H{{A}^{2}}}}=\frac{a\sqrt{3}}{4}$
| Bài tập 5: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân AB = BC = 3a, hình chiếu vuông góc của B’ lên mặt phẳng đáy trùng với trọng tâm tam giác ABC, mặt phẳng (ABB’A’) tạo với mặt phẳng (ABC) một góc 60°. Tính khoảng cách giữa 2 đường thẳng AB và B’C. |
Lời giải chi tiết
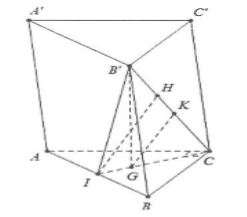
Dựng $CI\bot AB\Rightarrow I$ là trung điểm của AB.
Ta có: $(B'GI)\bot AB\Rightarrow \overset\frown{B'IG}={{60}^{\circ }}$
Lại có: $CI=\frac{1}{2}AB=\frac{3a\sqrt{2}}{2}\Rightarrow GI=\frac{a\sqrt{2}}{2}$
$\Rightarrow B'G=GI\tan {{60}^{\circ }}=\frac{a\sqrt{6}}{2}$
Dựng $IH\bot B'C\Rightarrow d(AB;B'C)=IH=\frac{B'G.CI}{B'C}$
Ta có: $B'C=\sqrt{B'{{G}^{2}}+G{{C}^{2}}}=\frac{a\sqrt{14}}{2}\Rightarrow IH=\frac{3a\sqrt{42}}{14}$
Do đó $d(AB;B'C)=IH=\frac{3a\sqrt{42}}{14}$
Hoặc dựng : $GK//IH\Rightarrow IH=\frac{3}{2}GK=\frac{3}{2}.\frac{B'G.GC}{\sqrt{B'{{G}^{2}}+G{{C}^{2}}}}$
TOÁN LỚP 12
