Cách tính Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song

Cách tính Khoảng cách giữa đường thẳng và mặt phẳng song song, giữa hai mặt phẳng song song
– Khoảng cách giữa đường thẳng và mặt phẳng song song
Khoảng cách giữa đường thẳng a và mặt phẳng $\left( \alpha \right)$ song song với nhau là khoảng cách từ một điểm M bất kì thuộc đường a đến mặt thẳng $\left( \alpha \right)$.
$d\left( a;\left( \alpha \right) \right)=d\left( M;\left( \alpha \right) \right)=MH\left( M\in \left( \alpha \right) \right)$.
– Khoảng cách giữa hai mặt phẳng song song
Khoảng cách giữa hai mặt phẳng song song là khoảng cách từ một điểm bất kì của mặt phẳng kia.
$d\left( \left( \alpha \right);\left( \beta \right) \right)=d\left( a;\left( \beta \right) \right)=d\left( A;\left( \beta \right) \right)=AH\left( a\subset \left( \alpha \right),A\in a \right)$
Bài tập tính khoảng cách giữa đường thẳng, mặt phẳng song song có đáp án
| Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt bên SBC vuông góc với đáy ABC, Gọi M, N, P lần lượt là trung điểm của AB, SA, AC. Tính khoảng cách giữa hai mặt phẳng $\left( MNP \right)$ và $\left( SBC \right)$. |
Lời giải chi tiết
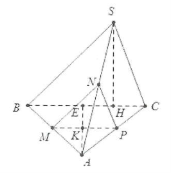
Do $\left\{ \begin{array} {} MP//BC \\ {} MN//SB \\ \end{array} \right.\Rightarrow \left( MNP \right)\bot \left( SBC \right)$
Dựng $SH\bot BC\left( H\in BC \right)$. Mặt khác $\left( SBC \right)\bot \left( ABC \right)$
Do đó $SH\bot \left( ABC \right)$
Gọi M là trung điểm của BC$\Rightarrow AM\bot BC$
Gọi $K=AE\cap MP\Rightarrow KE\bot BC$
Mặt khác $KE\bot SH\Rightarrow KE\bot (SBC)$
Suy ra $d\left( \left( MNP \right);\left( SBC \right) \right)=d\left( K;\left( SBC \right) \right)=KE=\frac{AE}{2}=\frac{a\sqrt{3}}{4}$
| Bài tập 2: Cho hình chóp tứ giác đều S.ABC có cạnh đáy băng 2a và cạnh bên đều bằng $a\sqrt{5}$. Tính khoảng cách giữa đường thẳng CD và mặt phẳng $\left( SAB \right)$. |
Lời giải chi tiết
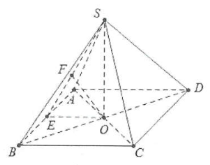
Gọi O là tâm của đáy ABCD$\Rightarrow SO\bot \left( ABCD \right)$
Ta có: $OA=\frac{AC}{2}=a\sqrt{2}$$\Rightarrow SO=\sqrt{S{{A}^{2}}-O{{A}^{2}}}=a\sqrt{3}$
Mặt khác $d\left( CD;\left( SAB \right) \right)=d\left( D;\left( SAB \right) \right)$
Ta có: $\frac{d\left( D;\left( SAB \right) \right)}{d\left( O;\left( SAB \right) \right)}=\frac{DB}{OB}=2$
Dựng $OE\bot AB,\text{OF}\bot \text{SE}$ ta có: $OE=\frac{AD}{2}=a$
Khi đó: $d\left( D;\left( SAB \right) \right)=2OF=2.\frac{SO.OE}{\sqrt{S{{O}^{2}}+O{{E}^{2}}}}=a\sqrt{3}$
| Bài tập 3: Cho hình lăng trụ ABC.A’B’C’ có tất cả các cạnh bên và cạnh đáy bằng a. Hình chiếu vuông góc của A’ trên $\left( ABC \right)$ trùng với trung điểm của BC.
a) Tính khoảng cách từ AA’ đến các mặt bên $\left( BCC'B' \right)$ b) Tính khoảng cách giữa hai mặt đáy của lăng trụ. |
Lời giải chi tiết
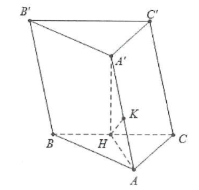
a) Gọi H là trung điểm của BC ta có: $A'H\bot BC$
Do $\Delta \text{ABC}$ đều nên $AH\bot BC\Rightarrow BC\bot \left( A'HA \right)$
Dựng $HK\bot \text{A}A'$ thì $\left\{ \begin{array} {} HK\bot BB' \\ {} KH\bot BC \\ \end{array} \right.\Rightarrow KH\bot \left( BCC'B' \right)$
Do đó $d\left( AA';\left( BCC'B' \right) \right)=d\left( K;\left( BCC'B' \right) \right)=KH$
Lại có: $AH=\frac{a\sqrt{3}}{2}\text{,AA}'=a\Rightarrow A'H=\sqrt{A'{{A}^{2}}-A{{H}^{2}}}=\frac{a}{2}$
Suy ra $HK=\frac{\text{AA }\!\!'\!\!\text{ }\text{.AH}}{\text{AA }\!\!'\!\!\text{ }}=\frac{a\sqrt{3}}{4}$
Do đó $d\left( AA';\left( BCC'B' \right) \right)=\frac{a\sqrt{3}}{4}$.
b) Ta có: $d\left( \left( ABC \right);\left( A'B'C' \right) \right)=d\left( A';\left( ABC \right) \right)=A'H=\frac{a}{2}$
| Bài tập 4: Cho hình lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a. Gọi M, N, P lần lượt là trung điểm của AD, DC và A’D’. Tính khoảng cách giữa hai mặt phẳng $\left( MNP \right)$ và $\left( ACC' \right)$. |
Lời giải chi tiết
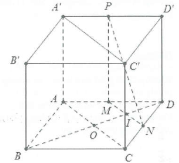
Ta có: $MN//AC,NP//AA'\Rightarrow \left( MNP \right)//\left( ACC'A' \right)$
Gọi O là tâm hình vuông ABCD và $I=DO\cap MN$
Ta có: $\left\{ \begin{array} {} IO\bot AC \\ {} IO\bot AA' \\ \end{array} \right.\Rightarrow IO\bot \left( ACC'A' \right)$
Do đó $d\left( \left( MNP \right);\left( ACC'A' \right) \right)=d\left( I;\left( ACC'A' \right) \right)=IO$
Lại có: $IO=\frac{OD}{2}=\frac{BD}{4}=\frac{a\sqrt{2}}{4}$
TOÁN LỚP 12
