Cách tính độ dài đoạn thẳng, góc giữa hai vectơ, chứng minh 2 đường thẳng vuông góc – Bài tập có đáp án chi tiết

Tính độ dài đoạn thẳng, góc giữa hai vectơ, chứng minh 2 đường thẳng vuông góc – Bài tập có đáp án
Phương pháp giải bài toán tính độ dài đoạn thẳng, góc giữa hai vecto, chứng minh hai đường thẳng vuông góc trong không gian
| Để tính độ dài đoạn thằng AB ta sử dụng công thức: $AB=\left| \overrightarrow{AB} \right|=\sqrt{{{\overrightarrow{AB}}^{2}}}$, để tính độ dài vectơ $\overrightarrow{u}$ ta sử dung công thức$\left| \overrightarrow{u} \right|=\sqrt{{{\overrightarrow{u}}^{2}}}$
Để tính góc giữa 2 vectơ ta sử dụng công thức: $\cos \left( \overrightarrow{a};\overrightarrow{b} \right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|}$ Để chứng minh 2 đường thẳng AB và CD vuông góc với nhau ta chứng minh: $\overrightarrow{AB}.\overrightarrow{CD}=0$ |
Bài tập về vecto trong không gian có đáp án chi tiết
| Bài tập 1: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và $BC=a\sqrt{2}$. Tính góc giữa hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{SC}$. |
Lời giải chi tiết
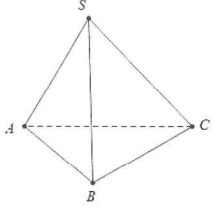
Do SB = SC = a; $BC=a\sqrt{2}$$\Rightarrow $ $\Delta SBC$vuông cân tại S.
Lấy điểm S làm điểm gốc ta phân tích: $\overrightarrow{AB}=\overrightarrow{SB}-\overrightarrow{SA}$
Ta có: $\overrightarrow{AB}.\overrightarrow{SC}=\left( \overrightarrow{SB}-\overrightarrow{SA} \right).\overrightarrow{SC}=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SC}$
$={{a}^{2}}.\cos {{90}^{0}}-{{a}^{2}}.\cos {{60}^{0}}=-\frac{{{a}^{2}}}{2}$
Do đó $\cos \left( \overrightarrow{AB};\overrightarrow{SC} \right)=\frac{\overrightarrow{AB}.\overrightarrow{SC}}{AB.SC}=\frac{-\frac{{{a}^{2}}}{2}}{a.a}=-\frac{1}{2}$
$\left( \overrightarrow{AB};\overrightarrow{SC} \right)={{120}^{0}}$
| Bài tập 2: Cho tứ diện ABCD.
a) Chứng minh rằng: $\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0$ b) Từ đẳng thức trên hãy suy ra nếu tứ diện ABCD có $AB\bot CD$ và $AC\bot DB$ thì $AD\bot BC$ |
Lời giải chi tiết
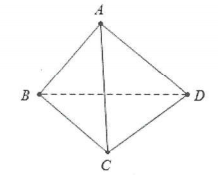
a) Lấy điểm A làm điểm gốc.
Ta có: $\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}$
$\overrightarrow{AB}.\left( \overrightarrow{AD}-\overrightarrow{AC} \right)+\overrightarrow{AC}\left( \overrightarrow{AB}-\overrightarrow{AD} \right)+\overrightarrow{AD}\left( \overrightarrow{AC}-\overrightarrow{AB} \right)=0$
b) Do $\overrightarrow{AB}.\overrightarrow{CD}+\overrightarrow{AC}.\overrightarrow{DB}+\overrightarrow{AD}.\overrightarrow{BC}=0$
Mặt khác: $\left\{ \begin{array} {} AB\bot CD \\ {} AC\bot DB \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array} {} \overrightarrow{AB}.\overrightarrow{CD}=0 \\ {} \overrightarrow{AC}.\overrightarrow{DB}=0 \\ \end{array} \right.\Rightarrow \overrightarrow{AD}.\overrightarrow{BC}=0$
Do đó $AD\bot BC$
| Bài tập 3: Cho tứ diện ABCD có AB = AC = AD và góc BAC = 600, góc BAD = 600, góc CAD = 900. Chứng minh rằng:
a) $AB\bot CD$ b) Nếu I và J lần lượt là trung điểm của AB và CD thì $IJ\bot AB$ |
Lời giải chi tiết
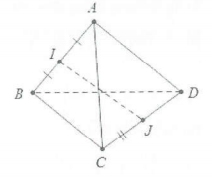
a) Lấy điểm A là điểm gốc ta có $\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}.\left( \overrightarrow{AD}-\overrightarrow{AC} \right)$
$=\overrightarrow{AB}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AC}={{a}^{2}}\cos {{60}^{0}}-{{a}^{2}}\cos {{60}^{0}}=0\Rightarrow AB\bot CD$
b) Ta có: $\overrightarrow{IJ}=\left( \overrightarrow{IA}+\overrightarrow{AJ} \right)=-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\left( \overrightarrow{AC}+\overrightarrow{AD} \right)$
Do đó $\overrightarrow{IJ}.\overrightarrow{AB}=\left( -\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD} \right).\overrightarrow{AB}$
$=-\frac{1}{2}\left( -{{\overrightarrow{AB}}^{2}}+\overrightarrow{AC}.\overrightarrow{AB}+\overrightarrow{AD}.\overrightarrow{AB} \right)$
$=-\frac{1}{2}\left( -{{\overrightarrow{a}}^{2}}+{{a}^{2}}\cos {{60}^{0}}+{{a}^{2}}\cos {{60}^{0}} \right)=0\Rightarrow IJ\bot AB$
| Bài tập 4: Cho hình chóp S.ABC có SA = SB = SC và ASB = BSC = CSA. Chứng minh rằng $SA\bot BC$, $SB\bot AC$ và $SC\bot AB$ |
Lời giải chi tiết
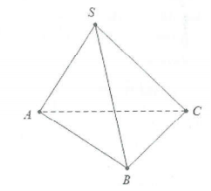
Giả sử $ASB=BSC=CSA=\alpha $và SA = SB = SC = a
Lấy điểm S làm điểm gốc ta có: $\overrightarrow{SA}.\overrightarrow{BC}=\overrightarrow{SA}.\left( \overrightarrow{SC}-\overrightarrow{SB} \right)$
$=\overrightarrow{SA}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SB}={{a}^{2}}\cos \alpha -{{a}^{2}}\cos \alpha =0$
Tương tự chứng mình trên ta cũng có $SB\bot AC$ và $SC\bot AB$
| Bài tập 5: Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của AB và CD. Biết rằng $AB\bot AC$, $AB\bot BD$. Chứng minh rằng AB và PQ vuông góc với nhau. |
Lời giải chi tiết
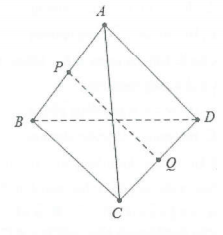
Ta có: $AB\bot AC,AB\bot BD\Rightarrow \left\{ \begin{array} {} \overrightarrow{AB}.\overrightarrow{AC}=0 \\ {} \overrightarrow{AB}.\overrightarrow{BD}=0 \\ \end{array} \right.$
Lại có: $\overrightarrow{PQ}=\overrightarrow{PA}+\overrightarrow{AQ}=-\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\left( \overrightarrow{AC}+\overrightarrow{AD} \right)$
Do đó $\overrightarrow{AB}.\overrightarrow{PQ}=\overrightarrow{AB}\left[ -\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\left( \overrightarrow{AC}+\overrightarrow{AD} \right) \right]$
$=\frac{{{\overrightarrow{AB}}^{2}}}{2}+\frac{\overrightarrow{AB}.\overrightarrow{AD}}{2}=\frac{\overrightarrow{AB}}{2}\left( \overrightarrow{AD}-\overrightarrow{AB} \right)=\frac{\overrightarrow{AB}}{2}.\overrightarrow{BD}=0$
Do đó $AB\bot PQ$
| Bài tập 6: Trong không gian cho 2 vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ tạo với nhau một góc ${{120}^{0}}$. Biết rằng $\left| \overrightarrow{a} \right|=3$ và $\left| \overrightarrow{b} \right|=5$. Tính $\left| \overrightarrow{a}+\overrightarrow{b} \right|$và $\left| \overrightarrow{a}-\overrightarrow{b} \right|$ |
Lời giải chi tiết
Ta có: ${{\left| \overrightarrow{a}+\overrightarrow{b} \right|}^{2}}={{\left( \overrightarrow{a}+\overrightarrow{b} \right)}^{2}}={{\overrightarrow{a}}^{2}}+2\overrightarrow{a}.\overrightarrow{b}+{{\overrightarrow{b}}^{2}}={{\left| \overrightarrow{a} \right|}^{2}}+2\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos \left( \overrightarrow{a};\overrightarrow{b} \right)+\left| \overrightarrow{b} \right|={{3}^{2}}+2.3.5.\cos {{120}^{0}}+{{5}^{2}}=19$
Do đó $\left| \overrightarrow{a}+\overrightarrow{b} \right|=\sqrt{19}$
Lại có: ${{\left| \overrightarrow{a}-\overrightarrow{b} \right|}^{2}}={{\left( \overrightarrow{a}-\overrightarrow{b} \right)}^{2}}={{\overrightarrow{a}}^{2}}-2\overrightarrow{a}.\overrightarrow{b}+{{\overrightarrow{b}}^{2}}={{\left| \overrightarrow{a} \right|}^{2}}-2\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|\cos \left( \overrightarrow{a};\overrightarrow{b} \right)+\left| \overrightarrow{b} \right|={{3}^{2}}-2.3.5.\cos {{120}^{0}}+{{5}^{2}}=49$
Do đó $\left| \overrightarrow{a}-\overrightarrow{b} \right|=7$
| Bài tập 7: Cho hình lập phương ABCD.A'B'C'D'. Tính góc giữa hai vectơ AC và DA'. |
Lời giải chi tiết
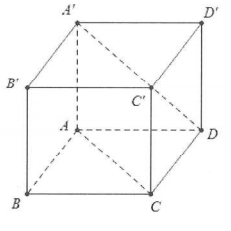
Ta có: $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ và $\overrightarrow{DA'}=\overrightarrow{DA}+\overrightarrow{DD'}=-\overrightarrow{AD}+\overrightarrow{AA'}$
Đặt $AB=a\Rightarrow AC=a\sqrt{2}=DA'$
Mặt khác $\overrightarrow{AC'}.\overrightarrow{DA'}=\left( \overrightarrow{AB}+\overrightarrow{AD} \right)\left( -\overrightarrow{AD'}+\overrightarrow{AA'} \right)=-A{{D}^{2}}=-{{a}^{2}}$
Suy ra $\cos \left( \overrightarrow{AC};\overrightarrow{DA'} \right)=\frac{-{{a}^{2}}}{2{{a}^{2}}}=-\frac{1}{2}\Rightarrow \left( \overrightarrow{AC};\overrightarrow{DA'} \right)=-{{120}^{0}}$
TOÁN LỚP 12
