Cách tìm thiết diện có yếu tố vuông góc – bài tập có đáp án chi tiết.

Cách tìm thiết diện có yếu tố vuông góc – bài tập có đáp án.

Dưới dây là một số bài tập tìm thiết diện vuông góc với đường thẳng cho trước có Lời giải chi tiết

Lời giải chi tiết

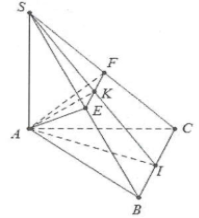
a) Gọi I là trung điểm của BC thì $AI\bot BC$

Mặt khác $SA\bot (ABC)\Rightarrow SA\bot BC\Rightarrow BC\bot (SAI)$

Thiết diện của khối chóp qua S và vuông góc với BC là tam giác SAI vuông tại A có $SA=a;AI=\frac{a\sqrt{3}}{2}$

Do đó ${{S}_{SAI}}=\frac{1}{2}SA.AI=\frac{{{a}^{2}}\sqrt{3}}{4}$

b) Dựng $AK\bot SI$, lại có $BC\bot (SAI)\Rightarrow BC\bot AK$

Suy ra $AK\bot (SBC)\Rightarrow AK\bot SI$

Qua K dựng đường thẳng vuông góc với SI cắt SB, SC lần lượt tại E và F $\Rightarrow$ thiết diện là tam giác AEF.

Ta có: $AK=\frac{SA.AI}{\sqrt{S{{A}^{2}}+A{{I}^{2}}}}=\frac{a\sqrt{21}}{7}$. Tam giác SAI vuông tại A có đường cao AH nên:

$S{{A}^{2}}=SK.SI\Rightarrow \frac{S{{A}^{2}}}{S{{I}^{2}}}=\frac{SK}{SI}=\frac{EF}{BC}=\frac{S{{A}^{2}}}{S{{A}^{2}}+A{{I}^{2}}}=\frac{4}{7}$

Do đó $EF=\frac{4}{7}a\Rightarrow {{S}_{AEF}}=\frac{1}{2}AK.EF=\frac{2{{a}^{2}}\sqrt{21}}{49}$

Lời giải chi tiết

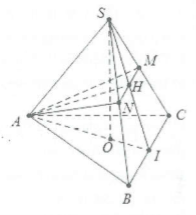
Gọi O là trọng tâm tam giác ABC thì $SO\bot (ABC)$ (Do S.ABC là khối chóp đều).

Gọi I là trung điểm của BC thì $AI\bot BC$mà $BC\bot SO$ suy ra $BC\bot (SAI)$

Dựng $AH\bot SI$, lại có $BC\bot (SAI)\Rightarrow BC\bot AH$

Suy ra $AH\bot (SBC)$. Qua K dựng đường thẳng song song với BC cắt SB, SC lần lượt tại N và M$\Rightarrow$ thiết diện là tam giác AMN.

Ta có: $SA=AI=\frac{a\sqrt{3}}{2}\Rightarrow$ H là trung điểm của SI

Suy ra $MN=\frac{1}{2}BC=\frac{a}{2}$. Lại có: $SI=\sqrt{S{{B}^{2}}-I{{B}^{2}}}=\frac{a\sqrt{2}}{2}\Rightarrow HI=\frac{a\sqrt{2}}{4}$

Khi đó $AH=\sqrt{A{{I}^{2}}-H{{I}^{2}}}=\frac{a\sqrt{10}}{4}\Rightarrow {{S}_{AMN}}=\frac{1}{2}AH.MN=\frac{{{a}^{2}}\sqrt{10}}{16}$

Lời giải chi tiết

a) Trong mặt phẳng (ABCD), qua M dựng đường thẳng vuông góc với AB cắt CD tại Q.

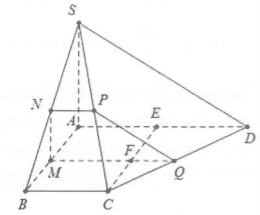
Trong mặt phẳng (SAB), qua M dựng đường thẳng vuông góc với AB cắt SB tại N.

Do $MQ\bot AB\Rightarrow MQ//BC$

Do đó (α) cắt (SBC) theo giao tuyến là NP (P $\in$SC) thì NP//BC. Do MN//SA $\Rightarrow MN\bot MQ$

Vậy thiết diện là hình thang MNPQ vuông tại M và N

Trong mp (ABCD), dựng $CE\bot AD$và cắt MQ tại F

b) Ta có:

$MF=AE=BC=a\Rightarrow DE=a;\frac{FQ}{ED}=\frac{CF}{CE}=\frac{BM}{BA}=\frac{a-x}{a}\Rightarrow FQ=a-x$

Suy ra $MQ=2a-x$, mặt khác $\frac{AM}{AB}=\frac{SN}{SB}=\frac{NP}{BC}\Rightarrow \frac{x}{a}=\frac{NP}{a}\Rightarrow NP=x$

Lại có: $\frac{MN}{SA}=\frac{BM}{BA}=\frac{a-x}{a}\Leftrightarrow MN=2a-2x$

Diện tích thiết diện là: ${{S}_{MNPQ}}=\frac{MQ+NP}{2}.MN=2a(a-x)$

Lời giải chi tiết

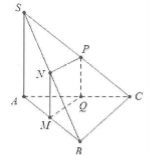
a) Trong mặt phẳng (ABCD), qua M dựng đường thẳng vuông góc với AB cắt AC tại Q.

Trong mặt phẳng (SAB), qua M dựng đường thẳng vuông góc với AB cắt SB tại N.

Do $MQ\bot AB\Rightarrow MQ//BC$

Do đó (α) cắt (SBC) theo giao tuyến là NP (P $\in$SC) thì NP//BC. Lại có: MN//SA $\Rightarrow$(α) cắt (SAC) theo giao tuyến là PQ $\Rightarrow$PQ//SA//MN$\Rightarrow$MNPQ là hình bình hành.

Do $MN//SA\Rightarrow MN\bot (ABC)\Rightarrow MN\bot AB$

Vậy thiết diện của chóp với (α) là hình chữ nhật MNPQ.

Ta có: $AB=BC=a\Rightarrow BC=a\sqrt{2}$

Mặt khác $\frac{AM}{AB}=\frac{MQ}{BC}=\frac{x}{a}\Rightarrow MQ=x,\frac{MN}{SA}=\frac{BM}{BA}=\frac{a-x}{a}\Rightarrow MN=\sqrt{3}(a-x)$

Diện tích thiết diện là ${{S}_{MNPQ}}=MN.MQ=\sqrt{3}x(a-x)$

Áp dụng bất đẳng thức: $a.b\le {{\left( \frac{a+b}{2} \right)}^{2}}$ta có: ${{S}_{MNPQ}}=MN.MQ=\sqrt{3}.x.(a-x)\le \sqrt{3}.{{\left( \frac{x+a-x}{2} \right)}^{2}}$

Suy ra ${{S}_{MNPQ}}\le \frac{\sqrt{3}}{4}{{a}^{2}}$ đạt được khi $x=a-x\Leftrightarrow x=\frac{a}{2}$

Lời giải chi tiết

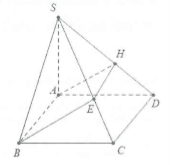
a) Trong mặt phẳng (SAD) dựng $AH\bot SD$ tại H. Ta có:

$\left\{ \begin{align}  & CD\bot AD \\  & SA\bot CD \\ \end{align} \right.\Rightarrow CD\bot (SAD)\Rightarrow CD\bot AH$

$\left\{ \begin{align}  & AH\bot CD \\  & AH\bot SD \\ \end{align} \right.\Rightarrow AH\bot (SCD)$

(α) là mặt phẳng chứa AB đồng thời chứa AH vuông góc với mặt phẳng (SCD). Vậy $(\alpha )\bot (SCD)$ và  $(\alpha )\equiv (AB,AH)$

Ta có: AB//CD nên CD//(α) và H là điểm chung của (α) và (SCD) nên giao tuyến của (α) và (SCD) là đường thẳng qua H và song song với CD cắt SC tại E. Ta có thiết diện của (α) và hình chóp S.ABCD là hình thang vuông AHEB vuông tại A và H vì $AB\bot (SAD)$

b) Do SA = AD = a $\Rightarrow$H là trung điểm của AD $\Rightarrow AH=\frac{AD}{2}=\frac{a\sqrt{2}}{2};EH=\frac{CD}{2}=\frac{a}{2}$

Diện tích hình thang vuông AHEB là: ${{S}_{AHEB}}=\frac{AB+EH}{2}.AH=\frac{a+\frac{a}{2}}{2}.\frac{a\sqrt{2}}{2}=\frac{3{{a}^{2}}\sqrt{2}}{8}$

Lời giải chi tiết

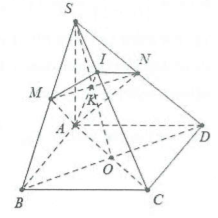
a) Gọi $I=(\alpha )\cap SC$. Ta có: $(\alpha )\bot SC,AI\subset (\alpha )\Rightarrow SC\bot AI$

Vậy AI là đường cao của tam giác vuông SAC. Trong mặt phẳng (SAC), đường cao AI cắt SO tại K và $AI\subset (\alpha )$ nên K là giao điểm của SO với (α).

b) Ta có: $\left\{ \begin{align}  & BD\bot AC \\  & BD\bot SA \\ \end{align} \right.\Rightarrow BD\bot (SAC)\Rightarrow BD\bot SC$

Mặt khác $BD\subset (SBD)$nên $(SBD)\bot (SAC)$

Do $BD\bot SC$ và $(\alpha )\bot SC$ nhưng BD không chứa trong (α) nên BD//(α).

c) Ta có:$K=SO\cap \left( \alpha  \right)$và SO thuộc mặt phẳng (SBD) nên K là một điểm chung của (α) và (SBD). Mặt phẳng (SBD) chứa BD//(α) nên cắt (α) theo giao tuyến d//BD. Giao tuyến này đi qua K là điểm chung của (α) và (SBD). Gọi M và N lần lượt là giao điểm của d với SB và SD. Thiết diện là tứ giác AMIN có $\left\{ \begin{align}  & AI\bot SC \\  & MN//BD \\ \end{align} \right.$

d) Ta có: $BD\bot (SAC)\Rightarrow BD\bot AI$mà $BD//MN\Rightarrow AI\bot MN$

Tứ giác AMIN có hai đường chéo vuông góc với nhau nên ${{S}_{AMIN}}=\frac{1}{2}AI.MN$

Ta có : $AC=a\sqrt{2}$ nên tam giác SAC cân tại A suy ra AI là đường cao đồng thời là đường trung tuyến. Khi đó $K=AI\cap SO$là trọng tâm tam giác SAC.

Lại có : $\frac{SK}{SO}=\frac{MN}{BD}=\frac{2}{3}\Rightarrow MN=\frac{2}{3}BD=\frac{2a\sqrt{2}}{3}$. Mặt khác $AI=\frac{SC}{2}=\frac{a\sqrt{2}}{2}$

Do đó ${{S}_{AMIN}}=\frac{1}{2}AI.MN=\frac{{{a}^{2}}}{3}$

Lời giải chi tiết

a) Ta có: $\left\{ \begin{align}  & CD\bot AD \\  & CD\bot SA \\ \end{align} \right.\Rightarrow CD\bot (SAD)$

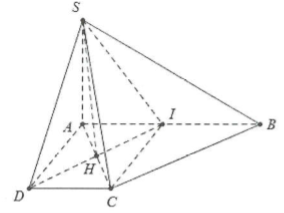
Suy ra $(SCD)\bot (SAD)$

Gọi I là trung điểm của đoạn AB. Ta có: AICD là hình vuông và IBCD là hình bình hành. Do DI//BC và $DI\bot AC\Rightarrow AC\bot CB$

Do đó $CB\bot (SAC)$

Vậy $(SBC)\bot (SAC)$

c) Ta có: $\left\{ \begin{align}  & DI\bot AC \\  & DI\bot SA \\ \end{align} \right.\Rightarrow DI\bot (SAC)$

Vậy mặt phẳng (α) chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI).

Do đó thiết diện của hình chóp S.ABCD với mặt phẳng (α) là tam giác đều SDI có $SD=DI=AI=a\sqrt{2}$

Diện tích tam giác SDI là: ${{S}_{SDI}}=\frac{S{{D}^{2}}\sqrt{3}}{4}=\frac{{{(a\sqrt{2})}^{2}}.\sqrt{3}}{4}=\frac{{{a}^{2}}\sqrt{3}}{2}$