Cách giải mọi dạng bài cực trị của hàm số bậc 3

CỰC TRỊ CỦA HÀM SỐ BẬC 3 – CÁCH GIẢI MỌI BÀI TẬP

Phương pháp giải bài tập tìm cực trị của hàm số bậc 3

Xét hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d\left( a\ne 0 \right).$

Ta có: $y'=3a{{x}^{2}}+2bx+c.$ Khi đó:

Hàm số có hai điểm cực trị (có cực đại cực tiểu) khi $y'=0$ có hai nghiệm phân biệt $\Leftrightarrow \Delta {{'}_{y'}}>0.$

Hàm số không có cực trị khi $y'=0$ vô nghiệm hoặc có nghiệm kép $\Leftrightarrow \Delta {{'}_{y'}}\le 0.$

Chú ý:

- Trong trường hợp hệ số $a$ chứa tham số ta cần xét $a=0.$

- Đối với hàm số bậc 3 ta luôn có ${{y}_{CD}}>{{y}_{CT}}$ và:

+) Nếu $a>0$ thì ${{x}_{CD}}<{{x}_{CT}}.$

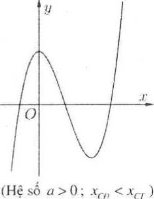
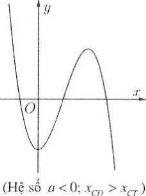
+) Nếu $a<0$ thì ${{x}_{CD}}>{{x}_{CT}}.$

Khi $y'=3a{{x}^{2}}+2bx+c=0$ có hai nghiệm phân biệt ta gọi $A\left( {{x}_{1}};{{y}_{1}} \right)$ và $B\left( {{x}_{2}};{{y}_{2}} \right)$ là tọa độ hai điểm cực trị thì theo định lý Viet ta có: $\left\{ \begin{matrix}   {{x}_{1}}+{{x}_{2}}=\frac{-2b}{3a}  \\   {{x}_{1}}{{x}_{2}}=\frac{c}{3a}\text{     }  \\\end{matrix} \right..$

Thực hiện phép chia đa thức $y$ cho $y'$ ta được $y=y'.g\left( x \right)+h\left( x \right).$

Khi đó ${{y}_{1}}=y'\left( {{x}_{1}} \right).g\left( {{x}_{1}} \right)+h\left( {{x}_{1}} \right)=h\left( {{x}_{1}} \right)$ và ${{y}_{2}}=y'\left( {{x}_{2}} \right).g\left( {{x}_{2}} \right)+h\left( {{x}_{2}} \right)=h\left( {{x}_{2}} \right)$

Do đó $\left\{ \begin{matrix}   {{y}_{1}}=h\left( {{x}_{1}} \right)  \\   {{y}_{2}}=h\left( {{x}_{2}} \right)  \\\end{matrix} \right..$

Vậy phương trình đường thẳng đi qua điểm cực đại và cực tiểu của đồ thị hàm số có dạng $y=h\left( x \right).$