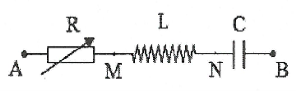
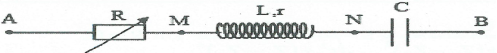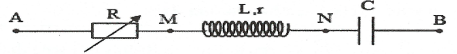Cách giải dạng bài mạch rlc có r thay đổi

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1. Mạch R-L-C có R thay đổi (các đại lượng khác không đổi)

HD giải:

a) Ta có: $I=\frac{U}{Z}=\frac{U}{\sqrt{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\le \frac{U}{\left| {{Z}_{L}}-{{Z}_{C}} \right|}$ khi $R=0$

Do đó ${{I}_{\max }}=\frac{U}{\left| {{Z}_{L}}-{{Z}_{C}} \right|}$ suy ra $\left\{ \begin{array}{} {{U}_{L\max }}={{Z}_{L}}.{{I}_{\max }}={{Z}_{L}}.\frac{U}{\left| {{Z}_{L}}-{{Z}_{C}} \right|} \\ {} {{U}_{C\max

}}={{Z}_{c}}.{{I}_{\max }}={{Z}_{c}}.\frac{U}{\left| {{Z}_{L}}-{{Z}_{C}} \right|} \\ \end{array} \right.$

b) ${{U}_{R}}=R.I=R.\frac{U}{\sqrt{{{R}^{2}}-{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{U}{\sqrt{1+{{\left( \frac{{{Z}_{L}}-{{Z}_{C}}}{R} \right)}^{2}}}}\to U$

c) Ta có: $P=R.{{I}^{2}}=R.\frac{{{U}^{2}}}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\frac{{{U}^{2}}}{R+\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R}}$

Theo bất đẳng thức $AM-GM$ ta có $R+\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R}\ge 2\sqrt{R.\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R}}=2\left| {{Z}_{L}}-{{Z}_{C}} \right|$

Khi đó $P\le \frac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}$ , dấu bằng xảy ra khi và chỉ khi $R=\left| {{Z}_{L}}-{{Z}_{C}} \right|$

Do đó ${{P}_{\max }}=\frac{{{U}^{2}}}{2R}=\frac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}$ khi $R=\left| {{Z}_{L}}-{{Z}_{C}} \right|$

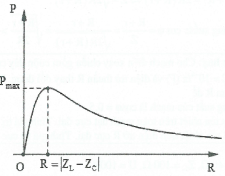
Dạng đồ thị

Ta có:

+) $R=0\Rightarrow P=0$

+) $R=\left| {{Z}_{L}}-{{Z}_{C}} \right|\Rightarrow P={{P}_{\max }}=\frac{{{U}^{2}}}{2R}$

+) $R\to +\infty \Rightarrow P\to 0$

2. Mạch R-Lr-C có R thay đổi (các đại lượng khác không đổi).

HD giải:

a) Ta có: $I=\frac{U}{Z}=\frac{U}{\sqrt{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}\le \frac{U}{\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$ khi $R=0$

Do đó ${{I}_{\max }}=\frac{U}{\sqrt{r+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$ suy ra $\left\{ \begin{array}{} {{U}_{L\max }}={{Z}_{L}}.{{I}_{\max }}={{Z}_{L}}.\frac{U}{\sqrt{r+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}} \\

{} {{U}_{C\max }}={{Z}_{C}}.{{I}_{\max }}={{Z}_{C}}.\frac{U}{\sqrt{r+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}} \\ \end{array} \right.$

b) Ta có :$P=\left( R+r \right){{I}^{2}}=\left( R+r \right).\frac{{{U}^{2}}}{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=\frac{{{U}^{2}}}{R+r+\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R+r}}$

$\Rightarrow P\le \frac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}$ (dấu bằng xảy ra khi và chỉ khi$R+r=\left| {{Z}_{L}}-{{Z}_{C}} \right|$) (với $r\le \left| {{Z}_{L}}-{{Z}_{C}} \right|$)

Chú ý: Trong trường hợp $r>\left| {{Z}_{L}}-{{Z}_{C}} \right|\Leftrightarrow {{P}_{\max }}$ khi $R=0$

c) Ta có: ${{P}_{R}}=R{{I}^{2}}=R.\frac{{{U}^{2}}}{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=R\frac{{{U}^{2}}}{{{R}^{2}}+2Rr+{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}$

$=\frac{{{U}^{2}}}{R+\frac{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{R}+2r}\le \frac{{{U}^{2}}}{2\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}+2r}}$

Vậy ${{P}_{\max }}=\frac{{{U}^{2}}}{2\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}+2r}}$ khi $R=\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}$

Khi đó

+) Tổng trở: ${{Z}^{2}}={{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{R}^{2}}+2Rr+\left[ {{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}} \right]$

$={{R}^{2}}+2Rr+{{R}^{2}}=2R\left( R+r \right)\Leftrightarrow Z=\sqrt{2R\left( R+r \right)}$

+) Hệ số công suất: $\cos \varphi =\frac{R+r}{Z}=\frac{R+r}{\sqrt{2R\left( R+r \right)}}=\sqrt{\frac{R+r}{2R}}>\frac{1}{\sqrt{2}}\Rightarrow \varphi <\frac{\pi }{4}$

Bài tập minh họa:

HD giải: Ta có ${{Z}_{L}}=40\Omega ,{{Z}_{C}}=100\Omega ,U=100V$

a) Hệ số công suất của mạch là $\cos \varphi =\frac{R+r}{Z}=\frac{1}{2}\Rightarrow \frac{R+r}{\sqrt{{{\left( R+r \right)}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}=\frac{1}{2}$

Thay số ta được: $\frac{R+50}{\sqrt{{{\left( R+50 \right)}^{2}}+{{\left( 60 \right)}^{2}}}}=\frac{1}{2}$

Giải phương trình trên ta được các nghiệm R cần tìm

b) Công suất tiêu thụ trên đoạn mạch đạt giá trị cực đại khi $R+r=\left| {{Z}_{L}}-{{Z}_{C}} \right|$

$\Leftrightarrow R+50=60\Rightarrow R=10\Omega$

Khi đó, công suất cực đại của mạch ${{P}_{\max }}=\frac{{{U}^{2}}}{2\left| {{Z}_{L}}-{{Z}_{C}} \right|}=\frac{250}{3}W$

c) Công suất tỏa nhiệt trên R cực đại khi $\left\{ \begin{array}{} R=\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}} \\ {} {{\left( {{P}_{R}} \right)}_{\max }}=\frac{{{U}^{2}}}{2r+\sqrt{{{r}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}} \\ \end{array} \right.$

Thay số ta được $R=10\sqrt{61}\Omega$ và ${{\left( {{P}_{R}} \right)}_{\max }}=\frac{{{100}^{2}}}{100+20\sqrt{61}}W$

3. Mạch R-L-C có R thay đổi (các đại lượng khác không đổi). Bài toán hai giá trị

HD giải: Ta có: $P=R{{I}^{2}}=R\frac{{{U}^{2}}}{{{R}^{2}}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}\Leftrightarrow {{R}^{2}}-\frac{{{U}^{2}}}{P}R+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}=0(*)$

Khi đó ${{R}_{1}}$ và ${{R}_{2}}$ là nghiệm của phương trình (*) (Do các đại lượng khác là hằng số).

Theo định lý Viet ta có: $\left\{ \begin{array}{} {{R}_{1}}+{{R}_{2}}=\frac{{{U}^{2}}}{P}\Rightarrow P=\frac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}} \\ {} {{R}_{1}}{{R}_{2}}={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}} \\ \end{array} \right.$

Với $R={{R}_{1}}$ ,ta có: $\tan {{\varphi }_{1}}=\frac{{{Z}_{L}}-{{Z}_{C}}}{{{R}_{1}}},\cos {{\varphi }_{1}}=\frac{{{R}_{1}}}{{{Z}_{1}}}=\frac{{{R}_{1}}}{\sqrt{{{R}_{1}}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}}$

$=\frac{{{R}_{1}}}{\sqrt{{{R}_{1}}^{2}+{{R}_{1}}{{R}_{2}}}}=\sqrt{\frac{{{R}_{1}}}{{{R}_{1}}+{{R}_{2}}}}$

Với $R={{R}_{2}}$ ,ta có: $\tan {{\varphi }_{2}}=\frac{{{Z}_{L}}-{{Z}_{C}}}{{{R}_{2}}},\cos {{\varphi }_{2}}=\sqrt{\frac{{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}}$

Suy ra $\tan {{\varphi }_{1}}.\tan {{\varphi }_{2}}=\frac{{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}{{{R}_{1}}{{R}_{2}}}=1\Rightarrow \left[ \begin{array}{} {{\varphi }_{1}}+{{\varphi }_{2}}=\frac{\pi }{2} \\ {} {{\varphi }_{1}}+{{\varphi }_{2}}=\frac{-\pi }{2} \\ \end{array} \right.$ hay $\left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|=\frac{\pi }{2}$

(Chú ý ${{\varphi }_{1}};{{\varphi }_{2}}$ cùng âm hoặc cùng dương)

Chú ý:

- Nếu mạch khuyết L hoặc C ta có: $\left[ \begin{array}{} {{R}_{1}}{{R}_{2}}=Z_{L}^{2} \\ {} {{R}_{1}}{{R}_{2}}=Z_{C}^{2} \\ \end{array} \right.$

- Cuộn dây không thuần cảm ta có: $\left[ \begin{array}{} \left( {{R}_{1}}+r \right)\left( {{R}_{2}}+r \right)={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}} \\ {} {{P}_{1}}={{P}_{2}}=\frac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}+2r} \\ \end{array} \right.$

- Gọi $\left\{ \begin{array}{} R={{R}_{1}} \\ {} R={{R}_{2}} \\ \end{array} \right.\Rightarrow {{P}_{1}}={{P}_{2}}$ và $R={{R}_{0}}$ khi đó $P={{P}_{\max }}$thì ${{R}_{1}}{{R}_{2}}=R_{0}^{2}={{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}$và khi đó

${{P}_{\max }}=\frac{{{U}^{2}}}{2{{R}_{0}}}=\frac{{{U}^{2}}}{2\sqrt{{{R}_{1}}{{R}_{2}}}}$

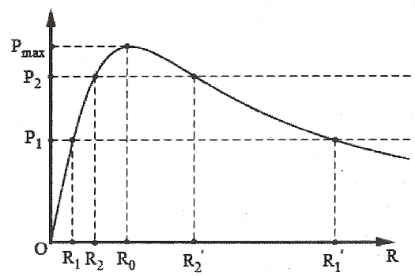
Đồ thị của cômg suất P theo R.

Ta có: $R_{0}^{2}={{R}_{1}}R_{1}^{'}={{R}_{2}}R_{2}^{'}=..={{R}_{n}}R_{n}^{'}$

(Trong đó ${{R}_{i}}$ và $R_{i}^{'}$ là 2 giá trị của R cho cùng một giá trị ${{P}_{i}}$).

Bài tập minh họa:

HD giải:

a) Theo chứng minh công thức ở trên, khi $\left\{ \begin{array}{} R={{R}_{1}},R={{R}_{2}} \\ {} \left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|=\frac{\pi }{2} \\ \end{array} \right.$

$\Rightarrow P={{P}_{1}}={{P}_{2}}-\frac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}=36W$

b) Ta có: $\left\{ \begin{array}{} R={{R}_{1}},R={{R}_{2}} \\ {} \left| {{\varphi }_{1}} \right|+\left| {{\varphi }_{2}} \right|=\frac{\pi }{2} \\ \end{array} \right.\Rightarrow {{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}={{R}_{1}}{{R}_{2}}=144\Rightarrow \left| {{Z}_{L}}-{{Z}_{C}} \right|=12$

Khi $R={{R}_{1}}=9\Omega$ thì ta có tổng trở của mạch là $Z=\sqrt{R_{1}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=15\Omega$

$\Rightarrow I=\frac{U}{Z}=2A$

Độ lệch pha của u và i thỏa mãn $\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{{{R}_{1}}}=\pm \frac{4}{3}\Rightarrow \varphi =\arctan \left( \pm \frac{4}{3} \right)={{\varphi }_{{}^{u}/{}_{i}}}$

$\Rightarrow {{\varphi }_{i}}=\arctan \left( \pm \frac{4}{3} \right)$

Từ đó, biểu thức cường độ dòng điện là $i=2\sqrt{2}\cos \left( 100\pi t\pm \arctan \left( \pm \frac{4}{3} \right) \right)A$

Khi $R={{R}_{2}}=16\Omega$ thì ta có tổng trở của mạch là $Z=\sqrt{R_{2}^{2}+{{\left( {{Z}_{L}}-{{Z}_{C}} \right)}^{2}}}=20\Omega$

$\Rightarrow I=\frac{U}{Z}=1,5A$

Độ lệch pha của u và i thỏa mãn $\tan \varphi =\frac{{{Z}_{L}}-{{Z}_{C}}}{{{R}_{1}}}=\pm \frac{3}{4}\Rightarrow \varphi =\arctan \left( \pm \frac{3}{4} \right)={{\varphi }_{{}^{u}/{}_{i}}}$

$\Rightarrow {{\varphi }_{i}}=\arctan \left( \pm \frac{3}{4} \right)$

Từ đó, biểu thức cường độ dòng điện là $i=1,5\sqrt{2}\cos \left( 100\pi t\pm \arctan \left( \pm \frac{3}{4} \right) \right)A$

c) Khi $C=\frac{{{10}^{-3}}}{2\pi }(F)\Rightarrow {{Z}_{C}}=20\Omega$.Mà $\left| {{Z}_{L}}-{{Z}_{C}} \right|=12\Omega \Leftrightarrow \left[ \begin{array}{} {{Z}_{L}}=32\Omega \\ {} {{Z}_{L}}=8\Omega \\ \end{array} \right.\Rightarrow \left[ \begin{array}{} L=\frac{8}{25\pi }H \\ {} L=\frac{2}{25\pi }H \\ \end{array} \right.$

d) Công suất cực đại của mạch khi R biến thiên được tính bởi ${{P}_{\max }}=\frac{{{U}^{2}}}{{{R}_{1}}+{{R}_{2}}}=37,5W$