Cách giải cực trị hình không gian hay – bài tập có đáp án chi tiết

Cách giải cực trị hình không gian hay – bài tập có đáp án

Phương pháp giải bài toán cực trị hình học không gian

• Áp dụng các phương pháp tính thể tích thông qua tam giác vuông; các loại góc và khoảng cách trong không gian cũng như các công thức tính thể tích khối chóp, khối lăng trụ.

• Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa biến.

Cách 1. Áp dụng bất đẳng thức AM – GM cho các số thực dương

- Dạng 2 số: $a+b\ge 2\sqrt{ab}\to ab\le \frac{{{a}^{2}}+{{b}^{2}}}{2}$ hoặc $ab\le \frac{{{\left( a+b \right)}^{2}}}{4}$

- Dạng 3 số: $a+b+c\ge 3\sqrt[3]{abc}\to abc\le \frac{{{a}^{3}}+{{b}^{3}}+{{c}^{3}}}{3}$ hoặc $abc\le \frac{{{(a+b+c)}^{3}}}{27}$

Cách 2. Khảo sát hàm số f(x) trên khoảng xác định (đạo hàm – lập bảng biến thiên)

Bài tập trắc nghiệm cực trị trong hình học không gian có đáp án

Lời giải chi tiết

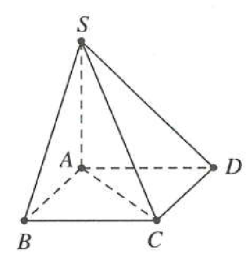
Đặt $AD=x\Rightarrow$ Diện tích hình chữ nhật ABCD là ${{S}_{ABCD}}=4x$

Tam giác ABC vuông tại B, có $AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{x}^{2}}+16}$

Tam giác SAC vuông tại A, có $SA=\sqrt{S{{C}^{2}}-A{{C}^{2}}}=\sqrt{20-{{x}^{2}}}$

Do đó, thể tích khối chóp S.ABCD là

${{V}_{S.ABCD}}=\frac{1}{3}.SA.{{S}_{ABCD}}=\frac{1}{3}.\sqrt{20-{{x}^{2}}}.4x=\frac{4}{3}x.\sqrt{20-{{x}^{2}}}$

Ta có $x.\sqrt{20-{{x}^{2}}}\le \frac{{{x}^{2}}+{{\left( \sqrt{20-{{x}^{2}}} \right)}^{2}}}{2}=\frac{20}{2}=10\Rightarrow V\le \frac{40}{3}$

Dấu bằng xảy ra khi $x=\sqrt{20-{{x}^{2}}}\Leftrightarrow x=\sqrt{10}$. Vậy ${{V}_{\text{max}}}=\frac{40}{3}$. Chọn A

Lời giải chi tiết

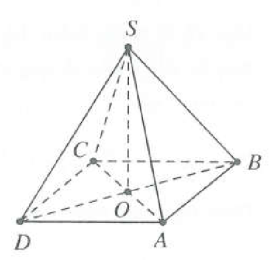
Vì $SA=SB=SC=SD\Rightarrow$ Hình chiếu của S trên mặt phẳng (ABCD) là tâm đường tròn ngoại tiếp đáy $\Rightarrow SO\bot \left( ABCD \right)$

Đặt $AB=x$. Ta có $BD=\sqrt{A{{B}^{2}}+A{{D}^{2}}}=\sqrt{{{x}^{2}}+16}$

Tam giác SBO vuông tại O, có

$SO=\sqrt{S{{B}^{2}}-O{{B}^{2}}}=\sqrt{36-\frac{{{x}^{2}}+16}{4}}=\frac{\sqrt{128-{{x}^{2}}}}{2}$

Do đó, thể tích khối chóp S.ABCD là

${{V}_{S.ABCD}}=\frac{1}{3}.SO.{{S}_{ABCD}}=\frac{1}{3}.\frac{\sqrt{128-{{x}^{2}}}}{2}.4x=\frac{2}{3}.x\sqrt{128-{{x}^{2}}}$

Mà $x\sqrt{128-{{x}^{2}}}\le \frac{{{x}^{2}}+128-{{x}^{2}}}{2}=64\to V\le \frac{2}{3}.64=\frac{128}{3}$. Vậy ${{V}_{\text{max}}}=\frac{128}{3}$. Chọn C

Lời giải chi tiết

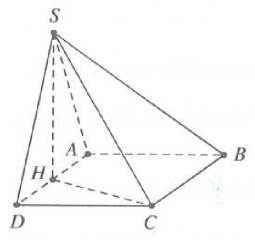
Gọi H là trung điểm AD. Tam giác SAD cân tại S $\Rightarrow SH\bot AD$

Ta có $\left( SAD \right)\bot \left( ABCD \right)\Rightarrow SH\bot \left( ABCD \right)\Rightarrow V=\frac{1}{3}.SH.{{S}_{ABCD}}$

Đặt $AD=2x\to {{S}_{ABCD}}=AB.AD=8x$

Tam giác HCD vuông tại D, có $HC=\sqrt{H{{D}^{2}}+C{{D}^{2}}}=\sqrt{{{x}^{2}}+16}$

Tam giác SHC vuông tại H, có $SH=\sqrt{S{{C}^{2}}-H{{C}^{2}}}=\sqrt{20-{{x}^{2}}}$

Do đó $V=\frac{1}{3}.\sqrt{20-{{x}^{2}}}.8x=\frac{8}{3}x.\sqrt{20-{{x}^{2}}}\le \frac{8}{3}.\frac{{{x}^{2}}+20-{{x}^{2}}}{2}=\frac{80}{3}$

Dấu bằng xảy ra khi $x=\sqrt{20-{{x}^{2}}}\Leftrightarrow x=\sqrt{10}$. Vậy ${{V}_{\text{max}}}=\frac{80}{3}$. Chọn D

Lời giải chi tiết

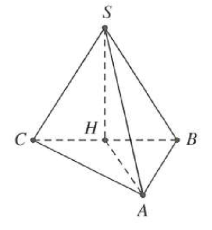
Gọi H là trung điểm BC, $\Delta ABC$ vuông tại A

Suy ra H là tâm đường tròn ngoại tiếp $\Delta ABC$

Vì $SA=SB=SC\Rightarrow H$ là hình chiếu của S trên (ABC)

Đặt $AC=x$. Tam giác ABC vuông $\Rightarrow BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{x}^{2}}+1}$

Diện tích tam giác ABC là ${{S}_{\Delta ABC}}=\frac{1}{2}.AB.AC=\frac{x}{2}$

Tam giác SBH vuông tại H, có $SH=\sqrt{S{{B}^{2}}-B{{H}^{2}}}=\frac{\sqrt{15-{{x}^{2}}}}{2}$

Do đó, thể tích cần tính là $V=\frac{1}{3}.SH.{{S}_{\Delta ABC}}=\frac{1}{12}x.\sqrt{15-{{x}^{2}}}$

Mà $x\sqrt{15-{{x}^{2}}}\le \frac{{{x}^{2}}+15-{{x}^{2}}}{2}=\frac{15}{2}\to V\le \frac{1}{12}.\frac{15}{2}=\frac{5}{8}.$Vậy ${{V}_{\text{max}}}=\frac{5}{8}$. Chọn B

Lời giải chi tiết

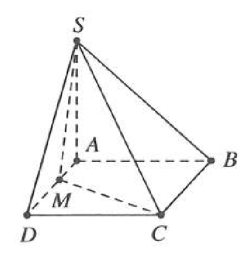
Từ giả thiết, ta có ${{x}^{2}}+{{y}^{2}}=1\Rightarrow y=\sqrt{1-{{x}^{2}}}$

Diện tích mặt đáy ${{S}_{ABCM}}=\left( \frac{AM+BC}{2} \right).AB=\frac{x+1}{2}$

Thể tích khối chóp ${{V}_{S.ABCM}}$ là ${{V}_{S.ABCM}}=\frac{1}{3}.SA.{{S}_{ABCM}}=\frac{\left( x+1 \right)\sqrt{1-{{x}^{2}}}}{6}$

Xét hàm số $f\left( x \right)=\left( x+1 \right)\sqrt{1-{{x}^{2}}}$ trên (0;1), có

${f}'\left( x \right)=\sqrt{1-{{x}^{2}}}-\frac{{{x}^{2}}+x}{\sqrt{1-{{x}^{2}}}}=\frac{1-x-2{{x}^{2}}}{\sqrt{1-{{x}^{2}}}};{f}'\left( x \right)=0\Leftrightarrow x=\frac{1}{2}$

Dựa vào bảng biến thiên, ta được $\underset{\left( 0;1 \right)}{\mathop{\text{max}}}\,f\left( x \right)=f\left( \frac{1}{2} \right)=\frac{3\sqrt{3}}{4}$. Vậy ${{V}_{\text{max}}}=\frac{\sqrt{3}}{8}$. Chọn B

Lời giải chi tiết

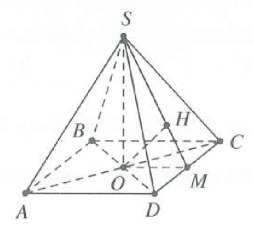
Gọi O là tâm hình vuông ABCD $\Rightarrow SO\bot \left( ABCD \right)$

Gọi M là trung điểm CD, H là hình chiếu của O trên SM

Ta có $\left\{ \begin{align}  & SO\bot CD \\  & OM\bot CD \\ \end{align} \right.\Rightarrow CD\bot \left( SMO \right)\Rightarrow CD\bot OH\Rightarrow OH\bot \left( SCD \right)$

Lại có $AB//CD\Rightarrow AB//\left( SCD \right)$

$\Rightarrow d\left( AB;SC \right)=d\left( A;\left( SCD \right) \right)=2d\left( O;\left( SCD \right) \right)$

Theo bài ra, ta có $d\left( AB;SC \right)=2OH=4\to OH=2$

Đặt $AB=2x\to OM=x$. Tam giác SMO vuông tại O, có $\frac{1}{O{{H}^{2}}}=\frac{1}{S{{O}^{2}}}+\frac{1}{O{{M}^{2}}}\Rightarrow SO=\frac{2x}{\sqrt{{{x}^{2}}-4}}$

Do đó, thể tích khối chóp S.ABCD là $V=\frac{1}{3}.SO.{{S}_{ABCD}}=\frac{1}{3}.\frac{2x}{\sqrt{{{x}^{2}}-4}}.4{{x}^{2}}=\frac{8}{3}.\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}-4}}$

Xét hàm số $f\left( x \right)=\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}-4}}$ trên $\left( 2;+\infty  \right)\to \max f\left( x \right)=6\sqrt{3}$

Vậy thể tích lớn nhất cần tính là ${{V}_{max}}=\frac{8}{3}.6\sqrt{3}=16\sqrt{3}$. Chọn D

Lời giải chi tiết

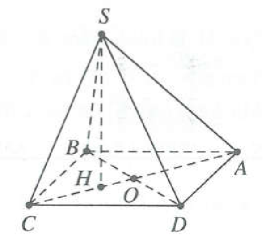
Gọi O là tâm hình thoi ABCD $\Rightarrow OA=OC$      (1)

Theo bài ra, ta có $\Delta SBD=\Delta CBD\Rightarrow SO=OC$  (2)

Từ (1) và (2), ta có $SO=OA=OC=\frac{1}{2}AC$

$\Rightarrow \Delta SAC$ vuông tại S $\Rightarrow AC=\sqrt{S{{A}^{2}}+S{{C}^{2}}}=\sqrt{{{x}^{2}}+1}$

Suy ra $OA=\frac{1}{2}AC=\frac{\sqrt{{{x}^{2}}+1}}{2}$ và $OB=\sqrt{A{{B}^{2}}-O{{A}^{2}}}=\frac{\sqrt{3-{{x}^{2}}}}{2}$

Diện tích hình thoi ${{S}_{ABCD}}=2.OA.OB=\frac{\sqrt{\left( {{x}^{2}}+1 \right)\left( 3-{{x}^{2}} \right)}}{2}$

Lại có $SB=SC=SD=1\Rightarrow$ Hình chiếu vuông góc H của đỉnh S trên mặt đáy là tâm đường tròn ngoại tiếp tam giác BCD $\to H\in AC$

Tam giác SAC vuông tại S, có $SH=\frac{SA.SC}{\sqrt{S{{A}^{2}}+S{{C}^{2}}}}=\frac{x}{\sqrt{{{x}^{2}}+1}}$

Do đó, thể tích cần tính là $V=\frac{1}{3}.SH.{{S}_{ABCD}}=\frac{1}{3}.\frac{\sqrt{\left( {{x}^{2}}+1 \right)\left( 3-{{x}^{2}} \right)}}{2}.\frac{x}{\sqrt{{{x}^{2}}+1}}=\frac{1}{6}x.\sqrt{3-{{x}^{2}}}$

Mà $x.\sqrt{3-{{x}^{2}}}\le \frac{{{x}^{2}}+3-{{x}^{2}}}{2}=\frac{3}{2}\to V\le \frac{1}{6}.\frac{3}{2}=\frac{1}{4}$. Vậy ${{V}_{\text{max}}}=\frac{1}{4}$. Chọn C

Lời giải chi tiết

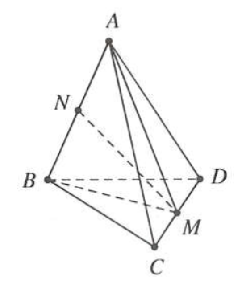
Gọi M, N lần lượt là trung điểm của CD, AB

Hai tam giác ACD, BCD đều $\Rightarrow AM=BM=2\sqrt{3}.\frac{\sqrt{3}}{2}=3$

$\Rightarrow \Delta ABM$ cân tại M $\Rightarrow MN\bot AB\Rightarrow MN=\sqrt{B{{M}^{2}}-B{{N}^{2}}}=\frac{\sqrt{36-{{x}^{2}}}}{2}$

Ta có $\left\{ \begin{align}  & BM\bot CD \\  & AM\bot CD \\ \end{align} \right.\Rightarrow CD\bot \left( ABM \right)\Rightarrow {{V}_{ABCD}}=2{{V}_{C.ABM}}=\frac{2}{3}.CM.{{S}_{\Delta ABM}}$

Do đó, thể tích cần tính là ${{V}_{ABCD}}=\frac{2}{3}.\frac{\sqrt{3}}{2}x.\frac{\sqrt{36-{{x}^{2}}}}{2}=\frac{\sqrt{3}}{6}x.\sqrt{36-{{x}^{2}}}$

Mà $x.\sqrt{36-{{x}^{2}}}\le \frac{{{x}^{2}}+36-{{x}^{2}}}{2}=18\to V\le \frac{\sqrt{3}}{6}.18=3\sqrt{3}$

Dấu bằng xảy ra khi $x=\sqrt{36-{{x}^{2}}}\Leftrightarrow 2{{x}^{2}}=36\Leftrightarrow x=3\sqrt{2}$. Chọn B

Lời giải chi tiết

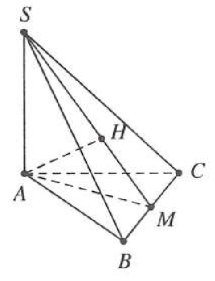
Gọi M là trung điểm BC, kẻ $AH\bot SM$    $(H\in SM)$

Tam giác ABC cân tại A suy ra $BC\bot AM$

Mà $SA\bot \left( ABC \right)\Rightarrow SA\bot BC$

Suy ra $BC\bot \left( SAM \right)\Rightarrow AH\bot BC\Rightarrow AH\bot \left( SBC \right)$

Do đó $d\left( A;\left( SBC \right) \right)=AH=3$. Tam giác AMH vuông $\Rightarrow AM=\frac{3}{\sin \alpha }$

Tam giác vuông cân ABC $\Rightarrow BC=2AM\Rightarrow {{S}_{\Delta ABC}}=\frac{9}{{{\sin }^{2}}\alpha }=\frac{9}{1-c\text{o}{{\text{s}}^{2}}\alpha }$

Khi đó, thể tích khối chóp là $V=\frac{1}{3}.SA.{{S}_{\Delta ABC}}=\frac{9}{\left( 1-co{{s}^{2}}\alpha  \right)cos\alpha }$

Xét hàm số $f\left( x \right)=\left( 1-co{{s}^{2}}x \right)\cos x$, ta được $f(x)\le \frac{2\sqrt{3}}{9}$. Suy ra $V\ge \frac{27\sqrt{3}}{2}$

Dấu bằng xảy ra khi và chỉ khi $cos\alpha =\frac{\sqrt{3}}{3}$. Chọn D

Lời giải chi tiết

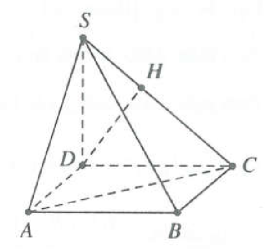
Gọi D là điểm sao cho ABCD là hình vuông

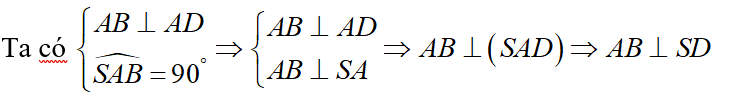
Tương tự, ta cũng có $BC\bot SD$ suy ra $SD\bot \left( ABCD \right)$

Kẻ $DH\bot SC$   $\left( H\in SC \right)\to DH\bot \left( SBC \right)$

Khi đó $d\left( A;\left( SBC \right) \right)=d\left( D;\left( SBC \right) \right)=DH$. Đặt $AB=x>0$

Tam giác SCD vuông tại D, có

$\frac{1}{D{{H}^{2}}}=\frac{1}{S{{D}^{2}}}+\frac{1}{D{{C}^{2}}}\Leftrightarrow \frac{1}{{{\left( \sqrt{2} \right)}^{2}}}=\frac{1}{S{{D}^{2}}}+\frac{1}{{{x}^{2}}}\Rightarrow SD=\frac{x\sqrt{2}}{\sqrt{{{x}^{2}}-2}}$

Do đó, thể tích khối chóp S.ABC là ${{V}_{S.ABC}}=\frac{1}{2}.{{V}_{S.ABCD}}=\frac{\sqrt{2}}{6}.\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}-2}}$

Xét hàm số $f\left( x \right)=\frac{{{x}^{3}}}{\sqrt{{{x}^{2}}-2}}$ trên $\left( \sqrt{2};+\infty  \right)$, ta được $\underset{\left( \sqrt{2};+\infty  \right)}{\mathop{\min }}\,f\left( x \right)=f\left( \sqrt{3} \right)=3\sqrt{3}$. Chọn A

Lời giải chi tiết

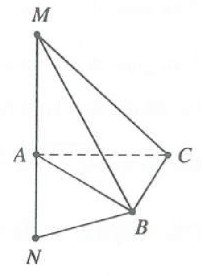
Đặt $AM=x,AN=y$ suy ra $AM.AN=x.y=1$

Tam giác ABC vuông cân tại B, có $AB=BC=\frac{AC}{\sqrt{2}}=\sqrt{2}$

Diện tích tam giác vuông ABC là ${{S}_{\Delta ABC}}=\frac{1}{2}AB.BC=1$

Ta có ${{V}_{MNBC}}={{V}_{M.ABC}}+{{V}_{N.ABC}}=\frac{1}{3}{{S}_{\Delta ABC}}.\left( AM+AN \right)=\frac{x+y}{3}$

Lại có $x+y\ge 2\sqrt{xy}$ (bất đẳng thức AM – GM) $\Rightarrow \frac{x+y}{3}\ge \frac{2}{3}$

Dấu bằng xảy ra khi $x=y=1$. Vậy ${{V}_{\text{min}}}=\frac{2}{3}$. Chọn C

Lời giải chi tiết

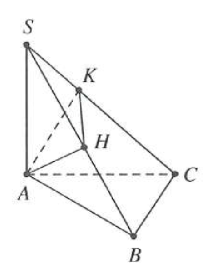
Đặt $AC=x$ $(0<x<2)$

Tam giác ABC vuông tại C $\Rightarrow BC=\sqrt{A{{B}^{2}}-A{{C}^{2}}}=\sqrt{4-{{x}^{2}}}$

Tam giác SAB vuông cân tại A, có đường cao AH $\Rightarrow SH=\frac{1}{2}SB$

Tam giác SAC vuông tại A, có $S{{A}^{2}}=SK.SC\Rightarrow \frac{SK}{SC}=\frac{S{{A}^{2}}}{S{{C}^{2}}}=\frac{4}{4+{{x}^{2}}}$

Ta có $\frac{{{V}_{S.AHK}}}{{{V}_{S.ABC}}}=\frac{SH}{SB}.\frac{SK}{SC}=\frac{1}{2}.\frac{4}{{{x}^{2}}+4}=\frac{2}{{{x}^{2}}+4}\Rightarrow {{V}_{S.AHK}}=\frac{2}{3}.\frac{x\sqrt{4-{{x}^{2}}}}{{{x}^{2}}+4}$

Xét hàm số $f\left( x \right)=\frac{2}{3}.\frac{x\sqrt{4-{{x}^{2}}}}{{{x}^{2}}+4}$ trên $\left( 0;2 \right)$, ta được $\underset{\left( 0;2 \right)}{\mathop{max}}\,f\left( x \right)=\frac{\sqrt{2}}{6}$. Chọn A

Lời giải chi tiết

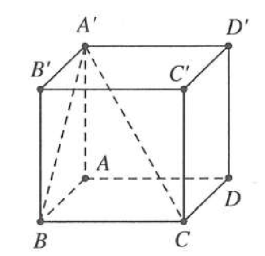
Ta có $B{B}'\bot BC$ và $AB\bot BC\Rightarrow BC\bot \left( AB{B}'{A}' \right)$

$\Rightarrow$ B là hình chiếu vuông góc của C trên $\left( AB{B}'{A}' \right)$

Suy ra $\widehat{{A}'C;\left( AB{B}'{A}' \right)}=\widehat{\left( {A}'C;{A}'B \right)}=\widehat{C{A}'B}=30{}^\circ$

Tam giác ${A}'BC$ vuông tại B, có $\tan \widehat{C{A}'B}=\frac{BC}{{A}'B}\Rightarrow {A}'B=3\sqrt{3}$

Tam giác ${A}'AB$ vuông tại A, có $A{A}'=\sqrt{{A}'{{B}^{2}}-A{{B}^{2}}}=\sqrt{27-{{x}^{2}}}$

Do đó thể tích khối hộp là ${{V}_{ABCD.{A}'{B}'{C}'{D}'}}=A{A}'.AB.AD=3x.\sqrt{27-{{x}^{2}}}$

Lại có $x.\sqrt{27-{{x}^{2}}}\le \frac{{{x}^{2}}+27-{{x}^{2}}}{2}=\frac{27}{2}\to {{V}_{ABCD.{A}'{B}'{C}'{D}'}}\le 3.\frac{27}{2}=\frac{81}{2}$

Dấu bằng xảy ra khi và chỉ khi $x=\sqrt{27-{{x}^{2}}}\Rightarrow x=\frac{3\sqrt{6}}{2}$. Chọn B

Lời giải chi tiết

Đặt $x=\frac{SK}{SC}$ $\left( 0\le x\le 1 \right)$ . Hình vẽ tham khảo

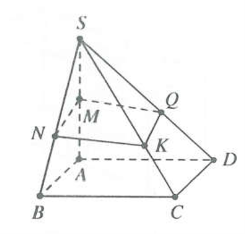
Vì mặt phẳng $\left( \alpha  \right)$ di động qua các điểm M, N và cắt các cạnh SC, SD lần lượt tại hai điểm phân biệt K, Q nên ta có $\frac{SA}{SM}+\frac{SC}{SK}=\frac{SB}{SN}+\frac{SD}{SQ}\Rightarrow 2+\frac{1}{x}=\frac{3}{2}+\frac{SD}{SQ}=\frac{2x}{2+x}$

Ta có $\frac{{{V}_{S.MNPQ}}}{{{V}_{S.ABCD}}}=\frac{1}{2}\left( \frac{SM}{SA}.\frac{SN}{SB}.\frac{SK}{SC}+\frac{SM}{SA}.\frac{SK}{SC}.\frac{SQ}{SD} \right)=\frac{1}{2}\left( \frac{4x}{3}-\frac{2}{x+2} \right)=\frac{2x}{3}-\frac{1}{x+2}$

Xét hàm số $f\left( x \right)=\frac{2x}{3}-\frac{1}{x+2}$ trên $\left[ 0;1 \right]$ ta được $\underset{\left[ 0;1 \right]}{\mathop{max}}\,f\left( x \right)=f\left( 1 \right)=\frac{1}{3}$

Vậy thể tích lớn nhất cần tính là ${{V}_{S.MNPQ}}=\frac{V}{3}$. Chọn C

Lời giải chi tiết

Sau khi cắt ở bốn góc hình vuông cạnh x, ta được khối hộp có

• Chiều cao bằng   cm

• Đáy là hình vuông cạnh   cm

Do đó, thể tích khối hộp chữ nhật là $V=x.{{\left( 18-2x \right)}^{2}}=\frac{1}{4}.4x.\left( 18-2x \right).\left( 18-2x \right)$

Ta có $4x.\left( 18-2x \right).\left( 18-2x \right)\le \frac{{{\left( 4x+18-2x+18-2x \right)}^{3}}}{27}=\frac{{{36}^{3}}}{27}=1728$