Cách giải các dạng toán về thời gian trong dao động cơ phần 3

Dạng 3: Xác định số lần vật qua một li độ x trong một khoảng thời gian cho trước
1. ĐẶT VẤN ĐỀ
Xét bài toán: Một vật dao động điều hòa với phương trình $x=A\cos \left( \omega t+\phi \right)$. Tính từ thời điểm t1, số lần vật đi qua vịt rí x trong khoảng thời gian$\Delta t$ là
2. PHƯƠNG PHÁP GIẢI
Trong một chu kì T vật đi qua vị trí có li độ $-A\text{ }<~x\text{ }<\text{ }A$ (ngoài hai vị trí biên) hai lần nếu không kể chiều của chuyển động. Nếu tính đến chiều của chuyển động thì sẽ đi qua một lần duy nhất.
Bước 1:
Tìm trạng thái tại thời điểm ban đầu t = t1 dựa vào pha ban đầu ta suy ra trạng thái của vật: $\left\{ \begin{array}{} {{x}_{1}}=? \\ {} \left[ \begin{array}{} {{v}_{1}}>0 \\ {} {{v}_{1}}<0 \\ \end{array} \right. \\ \end{array} \right.$
Bước 2:
Lấy $\frac{\Delta t}{T}$, tách $\Delta t=nT+\Delta {{t}^{'}}$
Bước 3:
Xác định trạng thái $\left( {{\mathbf{x}}_{\mathbf{2}}};{{\mathbf{v}}_{\mathbf{2}}} \right)$ (cũng chính là trạng thái của vật sau thời gian $\Delta {{t}^{'}}$), biểu diễn trên trục Ox (hoặc trên vòng tròn lượng giác) và tìm xem trong khoảng thời gian $\Delta {{t}^{'}}$ vật có đi qua vị trí có li độ x lần nào nữa hay không.
3. BÀI TẬP MINH HỌA DẠNG 3
| Bài tập 1: Một vật dao động điểu hòa dọc theo trục Ox với phương trình $x=5\cos \left( 4\pi t+\frac{\pi }{6} \right)(cm)$. Số lần vật đi qua vị trí có li độ $x\text{ }=-2,5\text{ }cm$ trong 6,13s đầu tiên là.
A. 21 B. 14 C. 25 D. 27 |
Lời giải chi tiết
Ta có $T=\frac{2\pi }{\omega }=-,5s\Rightarrow \frac{\Delta t}{T}=12,26\Rightarrow \Delta T=12T+0,13s$
Tại t = 0 vật có trạng thái: $\left\{ \begin{array}{} x=2,5\sqrt{3} \\ {} v<0 \\ \end{array} \right.$
Tại thời điểm t = 6,13 vật có trạng thái $\left\{ \begin{array}{} x=-2,767 \\ {} v<0 \\ \end{array} \right.$
Biểu diễn trên trục Ox

Do đó vật qua vị trí có li độ $x\text{ }=\text{ }-2,5\text{ }cm$ tổng cộng là $12.2+1\text{ }=25$lần. Chọn C.
| Bài tập 2: Một vật dao động điểu hòa dọc theo trục Ox với phương trình $x=5\cos \left( 4\pi t+\frac{\pi }{6} \right)(cm)$( t tính bằng s). Trong 7,75s đầu tiên vật qua vịt rí có li độ $x\text{ }=1\text{ }cm$ bao nhiêu lần.
A. 31 lần B. 30 lần C. 28 lần D. 14 lần |
Lời giải chi tiết
Tại thời điểm ban đầu vật có $\left\{ \begin{array}{} x=2cm \\ {} v>0 \\ \end{array} \right.$
Lại có : $\frac{\Delta t}{T}=15,5\Rightarrow \Delta t=15T+\frac{T}{2}$
Trong thời gian $\frac{T}{2}$ cuối vật đến vị trí $\left\{ \begin{array}{} x=-2cm \\ {} v<0 \\ \end{array} \right.$

Do đó vật qua vị trí có li độ $x\text{ }=\text{ }1\text{ }cm$ tổng cộng là $15.2+1\text{ }=\text{ }31$ lần. Chọn A
| Bài tập 3: Một chất điểm dao động điều hòa với gia tốc cực đại bằng $8{{\pi }^{2}}$cm/s2 và chu kì bằng 2s. Thời điểm ban đầu, t = 0 chất điểm có vận tốc $4\sqrt{3\pi }$ cm/s và đang tăng. Trong quãng thời gian 5,5s tính từ thời điểm ban đầu, chất điểm đi qua vị trí cách VTCB một khoảng bằng 8cm bao nhiêu lần?
A. 4 B. 5 C. 6 D. 7 |
Lời giải chi tiết
Viết phương trình vận tốc $\Rightarrow $ pt ly độ kết hợp vịt rí và thời điểm đi qua $\Rightarrow $ số lần N
$T=2s\Rightarrow \omega =\pi rad/s;{{a}_{\max }}=\omega .{{v}_{\max }}\Rightarrow {{v}_{\max }}=8\pi cm/s$
$v(t=0)=4\sqrt{3}$, đang tăng $(M)\Rightarrow \phi =-\pi /6$
$\Rightarrow v=8\pi .\cos (\pi t-\pi /6)\Rightarrow A=8\pi /\pi =8cm$
$\Rightarrow x=8\pi .\cos (\pi t-\pi /6-\pi /2)=8\cos (\pi t-2\pi /3)cm$
Vị trí cần xét có $\left| x \right|=8\Rightarrow x=\pm 8cm$: 2 vịt rí biên $\Rightarrow $ 1 T đi qua 2 lần
Tách $t=5,5s=2.2+1,5=2T+1,5s\Rightarrow \alpha =2.2\pi +\frac{3\pi }{2}$
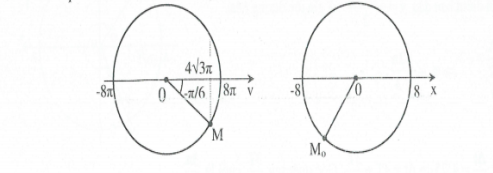
$\Rightarrow $ Số lần đi qua $N\text{ }=\text{ }2.2+1\text{ }=\text{ }5$ lần. Chọn B
| Bài tập 4: Một chất điểm dao động điều hòa với gia tốc cực đại bằng $4{{\pi }^{2}}$cm/s2 và chu kì bằng $T=2s$. Tại thời điểm ban đầu, chất điểm có vận tốc $v=2\pi \sqrt{3}$ cm/s và đang tăng. Trong quãng thời gian 41,5s chất điểm có tốc độ bằng một nữa tốc độ cực đại bao nhiêu lần
A. 43 lần B. 44 lần C. 82 lần D. 81 lần |
Lời giải chi tiết
Ta có: $\omega =\frac{2\pi }{T}=\pi (rad/s)\Rightarrow A=\frac{{{a}_{\max }}}{{{\omega }^{2}}}=4(cm)$

Do đó ${{v}_{\max }}=4\pi cm/s$. Khi $v=2\pi \sqrt{3}cm/s$ và đang tăng thì $\left\{ \begin{array}{} x=\frac{-A}{2}=-2cm \\ {} v>0 \\ \end{array} \right.$.
Khi đó ${{\phi }_{1}}=\frac{-2\pi }{3}$
Lại có $\left| v \right|=\frac{{{v}_{\max }}}{2}\Leftrightarrow \left| x \right|=\frac{A\sqrt{3}}{2}=2\sqrt{3}$
Mặt khác $\frac{\Delta t}{T}=20,75\Rightarrow \Delta t=20T+\frac{3}{4}T\Rightarrow $ góc quét sau $\frac{3}{4}T$ là $\frac{3}{2}\pi $
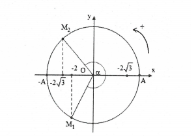
Suy ra ${{\phi }_{2}}={{\phi }_{1}}+1,5\pi =\frac{5\pi }{6}$ suy ra $\left\{ \begin{array}{} {{x}_{2}}=-2\sqrt{3} \\ {} {{v}_{2}}<0 \\ \end{array} \right.$
Do đó số lần mà $\left| x \right|=2\sqrt{3}$ là 20.4+2=82 lần. Chọn C
| Bài tập 5: Một vật dao động điểu hòa dọc theo trục Ox với biên độ A = 4cm và chu kì T =0,4s. Tại thời điểm ban đầu vật có vận tốc $v=20\pi \sqrt{3}$cm/s và gia tốc dương. Hỏi sau khoảng thời gian là 1,9s vật đi qua vị trí có li độ x = -3,5 cm bao nhiêu lần
A. 4 lần B. 8 lần C. 10 lần D. 6 lần |
Lời giải chi tiết
Ta có: $\omega =\frac{2\pi }{T}=5\pi (rad/s)$
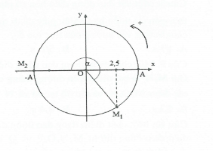
Tại thời điểm ban đầu $v=\frac{{{v}_{\max }}\sqrt{3}}{2}$ và gia tốc dương nên $\left\{ \begin{array}{} x=\frac{A}{2}=-2 \\ {} v>0 \\ \end{array} \right.\Rightarrow {{\phi }_{1}}=-\frac{2\pi }{3}$
Lại có : $\frac{\Delta t}{T}=4,75\Rightarrow \Delta t=4T+\frac{3T}{4}\Rightarrow $ Góc quét sau $\frac{3T}{4}$ cuối là $\frac{3\pi }{2}$
Do đó ${{\phi }_{2}}=\frac{5\pi }{6}\Rightarrow \left\{ \begin{array}{} {{x}_{2}}=-2\sqrt{3}=-3,464 \\ {} {{v}_{2}}<0 \\ \end{array} \right.$
Suy ra $\frac{3T}{4}$ cuối vật không qua vị trí có li độ x = -3,5 cm. Vậy n = 4.2 = 8 lần. Chọn B
| Bài tập 6: Một vật dao động điểu hòa dọc theo trục Ox với biên độ A = 45cm và chu kì T = 0,5s. Tại thời điểm ban đầu vật có gia tốc $a=-40{{\pi }^{2}}$cm/s2 và đang ra xa vị trí cân bằng. Hỏi sau khoảng thời gian là $\frac{7}{3}s$vật đi qua vị trí có li độ thõa mãn $\left| v \right|=\omega \left| x \right|$bao nhiêu lần?
A. 9lần B. 8 lần C. 17 lần D. 18 lần |
Lời giải chi tiết
Ta có: $\omega =4\omega (rad/s)$
Tại thời điểm ban đầu$\left\{ \begin{array}{} x=\frac{-a}{{{\omega }^{2}}}=2,5cm \\ {} v>0 \\ \end{array} \right.\Leftrightarrow {{\phi }_{1}}=\frac{-\pi }{3}$
Mặt khác ta có: $\Delta t=4T+\frac{2T}{3}$ suy ra góc quét sau cuối $\frac{4\pi }{3}\Rightarrow {{\phi }_{2}}=\pi $
Mặt khác $\left| v \right|=\omega \left| x \right|=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}\Leftrightarrow 2{{x}^{2}}={{A}^{2}}\Leftrightarrow \left| x \right|=\frac{A}{\sqrt{2}}$
Do đó trong $\frac{2T}{3}$ cuối vật qua vị trí $\left| x \right|=\frac{A}{\sqrt{2}}$ hai lần
Suy ra số lần vật có li độ $\left| x \right|=\frac{A}{\sqrt{2}}$ trong thời gian trên là n = 4.4+2 = 18 lần. Chọn D
VẬT LÝ LỚP 12
