Cách giải các dạng toán tính quãng đường trong dao động cơ phần 1

Dạng 1: Tính quãng đường vật đi được trong khoảng thời gian cho trước
1. ĐẶT VẤN ĐỀ
Xét bài toán: Cho phương trình dao động của vật $x=A\cos \left( \omega t+\varphi \right)$. Quãng đường vật đi được trong khoảng thời gian từ ${{t}_{1}}$ đến ${{t}_{2}}$ là
1. PHƯƠNG PHÁP GIẢI
Sau 1 chu kỳ T, bất luận vật xuất phát ở đâu, vật sẽ trở về đúng vị trí cũ và đi được quãng đường bằng 4A, vật sẽ đi qua 1 vị trí bất kỳ 2 lần tính cho cả 2 chiều chuyển động.
Bước 1:
Tính khoảng thời gian $\vartriangle t={{t}_{2}}-{{t}_{1}}$.
Bước 2:
Tính $\frac{\vartriangle t}{T}$suy ra $\vartriangle t=nT+\vartriangle {t}'$( trong đó $\vartriangle {t}'<T$)
Bước 3:
Tính theo các trường hợp ở dưới
+) Nếu phép chia hết tức là $\vartriangle {t}'=0$ thì quãng đường vật đi được là S = n.4A .
+) Nếu phép chia có dư:
TH1: $\vartriangle {t}''=\frac{T}{2}+\vartriangle {t}''\Rightarrow {S}'=2A+{S}''$( trong đó${S}''$ là quãng đường vật đi được trong khoảng thời gian $\vartriangle {t}''$) suy ra $S=n.4A+2A+{S}''$.
TH2: $\vartriangle {t}''<\frac{T}{2}$ thì $S=n.4A+{S}'$( trong đó ${S}'$ là quãng đường vật đi được trong khoảng thời gian $\vartriangle {t}'$).
+) Thay $t={{t}_{1}}$suy ra ${{\varphi }_{1}}$ để tìm trạng thái $\left( {{x}_{1}};{{v}_{1}} \right)$của vật trên đường tròn lượng giác hoặc trục thời gian.
+) Thay $t={{t}_{2}}$suy ra ${{\varphi }_{2}}$ để tìm trạng thái $\left( {{x}_{1}};{{v}_{1}} \right)$của vật trên đường tròn lượng giác hoặc trục thời gian.
Biểu diễn trên đường tròn lượng giác hoặc trục thời gian để tìm ${S}'={{S}_{{{t}_{1}}\to {{t}_{2}}}}$.
Đặc biệt:
+) Quãng đường vật đi được trong khoảng thời gian $n.\frac{T}{2}(n\in \mathbb{N}*)$ luôn là s = n.2A .
+) Khi vật đang ở vị trí cân bằng hoặc biên thì sau khoảng thời gian $n.\frac{T}{4}(n\in \mathbb{N}*)$vật đi được quãng đường là s = n.A .
2. BÀI TẬP MINH HỌA DẠNG 1
| Bài tập 1: [Trích đề thi đại học năm 2014]. Một vật dao động điều hòa với phương trình $x=5\cos \omega t$(cm). Quãng đường vật đi được trong một chu kì là
A. 10 cm. B. 5 cm. C. 15 cm. D. 20 cm. |
Lời giải chi tiết
Ta có: S = 4A = 20 cm . Chọn D.
| Bài tập 2: [Trích đề thi đại học năm 2013]. Một vật dao động điều hòa với biên độ 4 cm và chu kì 2 s. Quãng đường vật đi được trong 4 s là
A. 64 cm. B. 16 cm. C. 32 cm. D. 8 cm. |
Lời giải chi tiết
Trong 4 s = 2T vật đi được quãng đường là s = 2.4A = 32 cm . Chọn C.
| Bài tập 3: Một vật dao động điều hòa dọc theo trục Ox với phương trình $x=4\cos \left( 4\pi t+\frac{\pi }{3} \right)$(cm). Từ thời điểm ban đầu đến thời điểm $t=\frac{43}{12}s$, quãng đường vật đi được là
A. 114 cm. B. 116 cm. C. 117,5 cm. D. 115,5 cm. |
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=0,5s$. Mặt khác $\frac{\vartriangle t}{T}=7+\frac{1}{6}\Rightarrow \vartriangle t=7T+\frac{T}{6}.$
Do đó: $S=7.4A+{S}'.$
Tại thời điểm ban đầu $\varphi =\frac{\pi }{3}\Rightarrow \left\{ \begin{array}{} x=2cm \\ {} v<0 \\ \end{array} \right.$.

Trong thời gian $\frac{T}{6}$ vật đi từ vị trí có li độ $x=2\to x=-2\Rightarrow {S}'=4cm$.
Do đó: S = 28.4 + 4 = 116 cm . Chọn B.
| Bài tập 4: Một vật dao động điều hòa với phương trình $x=4\cos \left( 20\pi t-\frac{5\pi }{6} \right)$cm. Tính độ dài quãng đường mà vật đi được trong thời gian từ ${{t}_{1}}=5s$ đến ${{t}_{2}}=6,325s$.
A. 213,46 cm. B. 209,46 cm. C. 206,53 cm. D. 208,53 cm. |
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=0,1s;\frac{\vartriangle t}{T}=13+\frac{1}{4}\Rightarrow \vartriangle t=13T+\frac{T}{4}.$
Tại thời điểm ${{t}_{1}}=5s\Rightarrow {{\varphi }_{1}}=-\frac{5\pi }{6}\Rightarrow \left\{ \begin{array}{} x=-2\sqrt{3} \\ {} v>0 \\ \end{array} \right.$.
Tại thời điểm ${{t}_{2}}\Rightarrow \left\{ \begin{array}{} {{x}_{2}}=4\cos \left( 20\pi .6,325-\frac{5\pi }{6} \right)=2 \\ {} v>0 \\ \end{array} \right.$.

Suy ra $S=13.4A+\left| 2+2\sqrt{3} \right|=213,46cm.$ Chọn A.
| Bài tập 5: Một vật dao động điều hòa với phương trình $x=10\cos \left( \frac{4\pi t}{3} \right)$(cm). Quãng đường vật đi được trong khoảng thời gian $\vartriangle t=38,5s$kể từ khi vật bắt đầu chuyển động là
A. 10,4 m. B. 10,35 m. C. 10,3 m. D. 10,25 m. |
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=1,5s;\frac{\vartriangle t}{T}=25+\frac{2}{3}\Rightarrow \vartriangle t=25T+\frac{2T}{3}.$
Tại thời điểm ban đầu x = A = 10 cm.
Tại thời điểm ${{t}_{2}}\Rightarrow \left\{ \begin{array}{} {{x}_{2}}=4\cos \left( 20\pi .6,325-\frac{5\pi }{6} \right)=-5 \\ {} v>0 \\ \end{array} \right..$

Suy ra S = 25.4A + 2A + 5 = 1025 cm. Chọn D.
| Bài tập 6: Một vật dao động điều hòa với biên độ A = 6 cm và gia tốc cực đại là $96{{\pi }^{2}}cm/s$. Tại thời điểm ban đầu vật đang ở vị trí có li độ x = -3cm và chuyển động theo chiều dương. Quãng đường vật đi được trong khoảng thời gian 4,6 s đầu tiên là
A. 221 cm. B. 222 cm. C. 223 cm. D. 224 cm. |
Lời giải chi tiết
Ta có: $\omega =\sqrt{\frac{{{a}_{\max }}}{A}}\Rightarrow \omega =4\pi \Rightarrow T=0,5s\Rightarrow \frac{\vartriangle t}{T}=9+\frac{1}{5}\Rightarrow \vartriangle t=9T+\frac{T}{5}.$
Góc quét sau khoảng thời gian $\frac{T}{5}$ là $\frac{2\pi }{5}$
Tại thời điểm ban đầu ${{\varphi }_{1}}=\frac{-2\pi }{3}\Rightarrow {{\varphi }_{2}}=\frac{-2\pi }{3}+\frac{2\pi }{5}=\frac{-4\pi }{15}.$
![]()
Do đó $\left\{ \begin{array}{} {{x}_{2}}=4,015 \\ {} v>0 \\ \end{array} \right.\Rightarrow S=9.4A+\left| 4,015+3 \right|=223cm.$ Chọn C.
| Bài tập 7: Một vật dao động điều hòa xung quanh vị trí cân bằng O. Ban đầu vật đi qua O theo chiều dương. Sau thời gian ${{t}_{1}}=0,2s$vật chưa đổi chiều chuyển động và vận tốc còn lại một nửa. Sau thời gian ${{t}_{2}}=0,7s$vật đã đi được 20 cm. Vận tốc ban đầu ${{v}_{0}}$ của vật là
A. 72,55 cm/s. B. 36,27 cm/s. C. 20,94 cm/s. D. 41,89 cm/s. |
Lời giải chi tiết
Thời gian vận tốc của vật từ $v=\frac{{{v}_{\max }}}{2}\Rightarrow x=\frac{A\sqrt{3}}{2}\Leftrightarrow t={{t}_{0\to \frac{A\sqrt{3}}{2}}}=\frac{T}{6}.$
Suy ra $\frac{T}{6}=0,2\Rightarrow T=1,2s$
Khi đó ${{t}_{2}}=\frac{7T}{12}=\frac{T}{2}+\frac{T}{12}\Rightarrow S=2A+\frac{A}{2}=20\Rightarrow A=8cm.$

Suy ra $A=8;\omega =\frac{2\pi }{T}=\frac{5\pi }{3}\Rightarrow {{v}_{0}}={{v}_{\max }}=\frac{40\pi }{3}=41,89\left( cm/s \right).$ Chọn D.
| Bài tập 8: Một vật dao động điều hòa với phương trình $x=4\sqrt{2}\cos \left( 5\pi t-\frac{3\pi }{4} \right)$cm. Quãng đường vật đi được từ thời điểm ${{t}_{1}}=\frac{1}{10}s$ đến ${{t}_{2}}=6s$ là
A. 331,4 cm. B. 360 cm. C. 337,5 cm. D. 333,8 cm. |
Lời giải chi tiết
Ta có: $T=\frac{2\pi }{\omega }=0,4s$.
Lại có: $\frac{\vartriangle t}{T}=14,75$ suy ra $\vartriangle t=14T+\frac{3}{4}T=14T+\frac{T}{8}+\frac{T}{2}+\frac{T}{8}.$
Tại thời điểm ${{t}_{1}}$, vật có: ${{\varphi }_{1}}=\frac{-\pi }{4}\Rightarrow \left\{ \begin{array}{} x=4cm \\ {} v>0 \\ \end{array} \right..$
Tại thời điểm ${{t}_{2}}$, vật có: $\left\{ \begin{array}{} x=-4\sqrt{2} \\ {} v>0 \\ \end{array} \right..$

Dựa vào hình vẽ ta có: $S=14.4A+2A+2\left( A-\frac{A}{\sqrt{2}} \right)=331,4cm.$ Chọn A.
| Bài tập 9: [Chuyên Quốc Học Huế năm 2017]. Một chất điểm dao động điều hòa trên trục Ox xung quanh gốc O với biên độ 6 cm và chu kì 2 s. Mốc để tính thời gian là khi vật đi qua vị trí x = 3 cm theo chiều dương. Khoảng thời gian để chất điểm đi được quãng đường 249 cm kể từ thời điểm ban đầu là
A. $\frac{62}{3}s.$ B. $\frac{125}{6}s.$ C. $\frac{61}{3}s.$ D. $\frac{127}{6}s.$ |
Lời giải chi tiết
Ta có: $S=10.4A+A+\frac{A}{2}.$

Dựa vào trục thời gian suy ra: $\vartriangle t=10T+\frac{T}{6}+\frac{T}{4}=\frac{125}{6}s.$ Chọn B.
| Bài tập 10: Một vật dao động điều hòa theo phương trình $x=4\cos \left( \omega t-\frac{2\pi }{3} \right)cm.$ Trong giây đầu tiên vật đi được quãng đường 6 cm. Hỏi trong giây thứ 2013 vật đi được quãng đường bao nhiêu?
A. 5 cm. B. 4 cm. C. 6 cm. D. 12 cm. |
Lời giải chi tiết
| Sử dụng đường tròn lượng giác: Ban đầu vật ở tại ${{M}_{0}}$.
$\Rightarrow $1s đầu ứng với $\alpha ={2\pi }/{3}\;\Rightarrow \omega ={2\pi }/{3}\;{rad}/{s}\;\Rightarrow T=3s$ Quãng đường vật đi được trong giây thứ 2013: $\vartriangle {{S}_{2013}}={{S}_{2013}}-{{S}_{2012}}$ Ta có: $2012s=671T-{T}/{3}\;\Leftrightarrow 671$ vòng - ${2\pi }/{3}\;\Rightarrow $tại ${{M}_{2012}}$ $2013s=671T\Rightarrow {{M}_{2013}}\equiv {{M}_{0}}$ $\Rightarrow \vartriangle {{S}_{2013}}={{S}_{2013}}-{{S}_{2012}}=2+2=4cm$. Chọn B. |
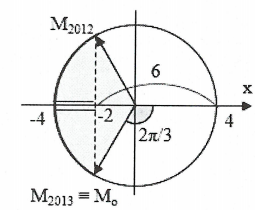 |
| Bài tập 11: Một vật dao động điều hòa theo phương trình $x=6\cos \left( \omega t-\frac{2\pi }{3} \right)cm.$ Trong giây đầu tiên vật đi được quãng đường 6 cm. Gọi x, y là quãng đường vật đi được trong giây thứ 2015 và trong giây thứ 2017. Chọn phương án đúng.
A. $2x-y=6cm.$ B. $x-y=3cm.$ C. $x+y=9cm.$ D. $x+y=6cm.$ |
Lời giải chi tiết
| Sử dụng đường tròn lượng giác. Ban đầu vật ở tại ${{M}_{0}}$.
$\Rightarrow $1s đầu ứng với $\alpha ={2\pi }/{3}\;\Rightarrow \omega ={2\pi }/{3}\;{rad}/{s}\;\Rightarrow T=3s$ Ta có: $2014s=671T+{T}/{3}\;\Leftrightarrow 671$ vòng + ${2\pi }/{3}\;\Rightarrow $tại ${{M}_{2014}}$ Cứ trong khoảng 1s vật quay được ${2\pi }/{3}\;$rad $\Rightarrow {{M}_{2015}},{{M}_{2016}},{{M}_{2017}}$ Qđ đi được trong giây thứ 2015: $x={{S}_{2015}}- {{S}_{2014}}=6cm$ Qđ đi được trong giây thứ 2017: $y={{S}_{2017}}-{{S}_{2016}}=6cm.$ $\Rightarrow 2x-y=6cm$thỏa mãn. Chọn A. |
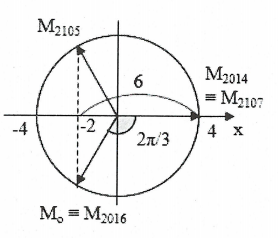 |
| Bài tập 12: Một vật dao động điều hòa theo phương trình $x=12\cos \left( \omega t-\frac{\pi }{3} \right)cm.$ Trong giây đầu tiên vật đi được quãng đường $\left( 18-6\sqrt{3} \right)cm$. Gọi x, y là quãng đường vật đi được trong giây thứ 2015 và giây thứ 2016. Chọn phương án đúng.
A. $2x-y=6cm.$ B. $x-y=3cm.$ C. $x+y=32,78cm.$ D. $x+y=24cm.$ |
Lời giải chi tiết
| Ban đầu vật ở ${{M}_{0}}$, 1s đầu có $s=18-6\sqrt{3}cm$ ứng với $\alpha =\frac{\pi }{2}$
$\Rightarrow {T}/{4=1\Rightarrow T=4s.}\;$ Tách $2014s=503T+{T}/{2\Rightarrow {{M}_{2014}}}\;$ Do cứ trong khoảng 1s vật quay được góc $\frac{\pi }{2}\Rightarrow {{M}_{2015}},{{M}_{2016}}.$ Qđ đi trong giây thứ 2015: $x={{S}_{2015}}-{{S}_{2014}}=18-6\sqrt{3}cm$ Qđ đi trong giây thứ 2016: $x={{S}_{2016}}-{{S}_{2015}}=6+6\sqrt{3}cm.$ $\Rightarrow x+y=24cm$ thỏa mãn. Chọn D.
|
 |
| Bài tập 13: Một dao động điều hòa có tần số f = 2 Hz. Gọi ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ là ba thời điểm ở đó vật có gia tốc ${{a}_{1}},{{a}_{2}},{{a}_{3}}$. Biết ${{a}_{1}}=-{{a}_{2}}=-{{a}_{3}}=20\frac{\sqrt{3}}{2}m/{{s}^{2}}$ và $\left( {{t}_{2}}-{{t}_{1}} \right)=2\left( {{t}_{3}}-{{t}_{2}} \right).$Quãng đường ngắn nhất vật đi từ ${{t}_{1}}$ đến ${{t}_{3}}$ bằng
A. 25 cm. B. 10 cm. C. $20\sqrt{2}$cm. D. $10\sqrt{2}$cm. |
Lời giải chi tiết
| Ta có:
${{x}_{1}}=-\frac{{{a}_{1}}}{{{\omega }^{2}}}=-\frac{20\sqrt{3}}{2.{{\left( 2\pi .2 \right)}^{2}}}=-0,0625\sqrt{3}m=-6,25\sqrt{3}cm$$\Rightarrow {{x}_{1}}=-{{x}_{2}}=-{{x}_{3}}=-6,25\sqrt{3}cm.$ +) 3 thời điểm ${{t}_{1}},{{t}_{2}},{{t}_{3}}$ không cho liên tiếp nên xảy ra 2 trường hợp: ${{x}_{1}}$ theo chiều dương${{M}_{1}}$ hoặc ${{x}_{1}}$ theo chiều âm ${{M}_{1}}^{\prime }$. Để quãng đường ${{t}_{1}}$ đến ${{t}_{3}}$ là ngắn nhất $\Rightarrow $${{x}_{1}}$ ứng với trạng thái ${{M}_{1}}$. +) Do $\left( {{t}_{2}}-{{t}_{1}} \right)=2\left( {{t}_{3}}-{{t}_{2}} \right)\Rightarrow $Cung ${{M}_{1}}{{M}_{2}}=2{{M}_{2}}{{M}_{3}}$ Mặt khác cung ${{M}_{1}}{{M}_{3}}={{M}_{1}}{{M}_{2}}+{{M}_{2}}{{M}_{3}}=\pi \Rightarrow $cung ${{M}_{2}}{{M}_{3}}={\pi }/{3}\;$ $\Rightarrow {{x}_{3}}=\frac{A\sqrt{3}}{2}=6,25\sqrt{3}\Rightarrow A=12,5cm$ $\Rightarrow $ Quãng đường ngắn nhất vật đi từ ${{t}_{1}}$ đến ${{t}_{3}}$ là: $S=2A=25cm.$ Chọn A. |
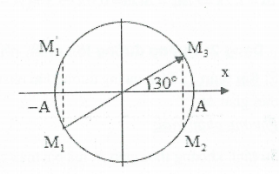 |
| Bài tập 14: Một vật dao động điều hòa có tần số f, biên độ A. Tại thời điểm ban đầu vật qua vị trí ${{x}_{1}}\ge 0$theo chiều dương sau đó $\vartriangle t\left( s \right)$vật đi được 5 cm mà chưa đổi chiều chuyển động, sau đó đi thêm một khoảng thời gian ${T}/{4}\;$thì vật đến vị trí có li độ 5 cm và đi tiếp $5\vartriangle t\left( s \right)$ thì hết một chu kỳ. Quãng đường vật đi trong khoảng thời gian $2,4\vartriangle t\left( s \right)$ tính từ thời điểm ban đầu có thể là?
A. 7,417 cm. B. 26,21 cm. C. 7,147 cm. D. A hoặc B. |
Lời giải chi tiết
| Từ ${{x}_{1}}$ đến ${{x}_{2}}$, ta có: ${{x}_{2}}-{{x}_{1}}=5cm$và $\alpha =\vartriangle t.\omega $
Từ ${{x}_{2}}$ đến ${{x}_{3}}$, ta có: ${{\alpha }_{2}}=T.{\omega }/{4}\;={\pi }/{2}\;\Rightarrow {{x}_{2}}^{2}+{{5}^{2}}={{A}^{2}}$ Từ ${{x}_{3}}$ đến ${{x}_{1}}$ đi hết một chu kỳ $\Rightarrow \vartriangle t+{T}/{4}\;+5\vartriangle t=T$ $\Rightarrow \vartriangle t={T}/{8}\;\Rightarrow \alpha ={{45}^{\circ }}$ Ta có: $\begin{array}{} \cos \alpha =\cos \left( \beta -\varphi \right)=\cos \beta .cos\varphi +sin\beta .sin\varphi \\ {} \Leftrightarrow \frac{1}{\sqrt{2}}=\frac{{{x}_{1}}}{A}.\frac{{{x}_{2}}}{A}+\sqrt{\left( 1-\frac{{{x}_{1}}^{2}}{{{A}^{2}}} \right)\left( 1-\frac{{{x}_{2}}^{2}}{{{A}^{2}}} \right)} \\ {} \Leftrightarrow {{\left( \frac{{{x}_{1.}}{{x}_{2}}}{{{A}^{2}}} \right)}^{2}}+\frac{1}{2}-\sqrt{2}.\frac{{{x}_{1.}}{{x}_{2}}}{{{A}^{2}}}={{\left( \frac{{{x}_{1.}}{{x}_{2}}}{{{A}^{2}}} \right)}^{2}}+1-\left( \frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{{A}^{2}}} \right) \\ {} \Rightarrow \left( \frac{{{x}_{1}}^{2}+{{x}_{2}}^{2}}{{{A}^{2}}} \right)-\sqrt{2}.\frac{{{x}_{1.}}{{x}_{2}}}{{{A}^{2}}}=0,5 \\ {} \Rightarrow {{x}_{1}}^{2}+{{x}_{2}}^{2}-\sqrt{2}.{{x}_{1.}}{{x}_{2}}=0,5\left( {{x}_{2}}^{2}+25 \right) \\ {} \Rightarrow {{\left( {{x}_{2}}-5 \right)}^{2}}+{{x}_{2}}^{2}-\sqrt{2}\left( {{x}_{2}}-5 \right){{x}_{2}}=0,5\left( {{x}_{2}}^{2}+25 \right) \\ {} \Rightarrow \left( \frac{3-2\sqrt{2}}{2} \right){{x}_{2}}^{2}+\left( 5\sqrt{2}-10 \right)x+12,5=0 \\ \end{array}$ $\Rightarrow {{x}_{2}}=5cm$và ${{x}_{2}}=29,14cm$ |
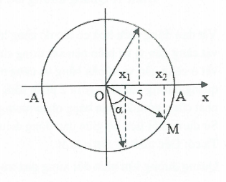 |
TH1:
$\begin{array}{} {{x}_{2}}=5cm\Rightarrow {{x}_{1}}=0\Rightarrow A=5\sqrt{2}cm \\ {} \vartriangle {t}'=2,4\vartriangle t\Rightarrow \vartriangle \alpha =\vartriangle {t}'.\omega =0,6\pi \Rightarrow S=A+\left( A-A\cos \left( 0,1\pi \right) \right)=7,417cm \\ \end{array}$
TH2:
${{x}_{2}}=29,41cm\Rightarrow {{x}_{1}}=24,14cm\Rightarrow A=29,57cm$
$\vartriangle t=1,2s\Rightarrow \vartriangle \alpha =\vartriangle t.\omega =0,6\pi \Rightarrow S=\left( A-{{x}_{1}} \right)+\left( A-A\cos 1,27 \right)=26,21cm.$
Chọn B.
VẬT LÝ LỚP 12
