Cách giải các dạng bài tìm vị trí các điểm dao động cực đại cực tiểu (CĐ CT)

CÁCH GIẢI CÁC DẠNG BÀI VỊ TRÍ CÁC ĐIỂM CỰC ĐẠI, CỰC TIỂU

Dạng 1: Vị trí các điểm dao động cực đại, cực tiểu trên AB.

Bài toán:

Tìm vị trí điểm M thuộc khoảng AB sao cho M gần ( hoặc xa ): A, B, hoặc I… nhất.

Phương pháp giải:

Đặt MB = x. Ta có: ${{d}_{2}}-{{d}_{1}}=MB-MA=x-\left( AB-x \right)=2x-AB=f\left( k \right)$

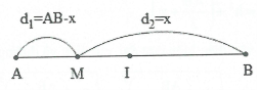
Suy ra $x=\frac{AB+f\left( k \right)}{2}$

Biện luận MB = x.

• TH1: Giải M gần B nhất: Cho $x=0\left( k\in \mathbb{Z} \right)$ tìm ${{x}_{\min }}>0.$

• TH2: Giải M gần A nhất (xa B nhất): Cho $x=AB\left( k\in \mathbb{Z} \right)$ tìm ${{x}_{\max }}<AB$.
• TH3: Giải M xa I nhất tương đương với M gần A hoặc gần B nhất.
• TH4: M gần I nhất: Cho $x=\frac{AB}{2}$ tìm $k\in \mathbb{Z}$.

Trong trường hợp này nếu M gần I nhất thuộc đoạn IB thì ta lấy giá trị $x<\frac{AB}{2}$.

Nếu M gần I nhất thuộc đoạn IA thì ta lấy giá trị $x>\frac{AB}{2}.$

Dạng 2: Vị trí các điểm cực đại cực tiểu trên đường thẳng vuông góc với AB

Phương pháp giải:

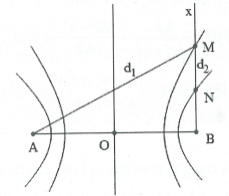
+) Đường (H) gần O nhất cắt Bx tại điểm xa B nhất.

+) Đường (H) gần B nhất cắt Bx tại điểm gần B nhất.

Tìm vị trí các điểm trên BO gần B hay xa B.

Tìm ${{d}_{2}}-{{d}_{1}}=f\left( k \right)$.

Tính ${{d}_{2}}-{{d}_{1}}$ tại B suy ra ${{k}_{B}}$.

Tính ${{d}_{2}}-{{d}_{1}}$ tại O suy ra ${{k}_{O}}$ từ đó suy ra ${{k}_{M}}$ và ${{k}_{N}}$.

Khi đó ta tính được ${{d}_{2}}-{{d}_{1}}=a$.

Giải hệ: $\left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=a \\ {} d_{1}^{2}=d_{2}^{2}+A{{B}^{2}} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=a \\ {} \left( {{d}_{1}}-{{d}_{2}} \right)({{d}_{1}}+{{d}_{2}})=A{{B}^{2}} \\ \end{array} \right.\Leftrightarrow \left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=d \\ {} {{d}_{2}}+{{d}_{1}}=\frac{A{{B}^{2}}}{a} \\ \end{array} \right.\Rightarrow {{d}_{1}};{{d}_{2}}.$

Hoặc giải PT: ${{d}_{2}}-\sqrt{d_{2}^{2}+A{{B}^{2}}}=a\Rightarrow {{d}_{2}}$.

Dạng 3: Vị trí cực đại cực tiểu trên đường $\Delta$ song song với AB.

Xác định đường Hypebol qua M, cắt $\Delta$. Đặt

OH = CM = x. Ta có:

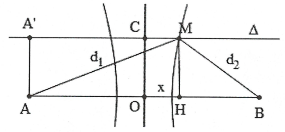
$\left\{ \begin{array}{} d_{2}^{2}={{h}^{2}}+{{\left( \frac{AB}{2}-x \right)}^{2}} \\ {} d_{1}^{2}={{h}^{2}}+{{\left( \frac{AB}{2}+x \right)}^{2}} \\ \end{array} \right.\left( h=OC \right)$

Dựa vào điều kiện cực đại, cực tiểu và đường Hypebol ta có: ${{d}_{1}}-{{d}_{2}}=f\left( k \right)=a$ (xác định).

Khi đó $\sqrt{{{h}^{2}}+{{\left( \frac{AB}{2}-x \right)}^{2}}}-\sqrt{{{h}^{2}}+{{\left( \frac{AB}{2}+x \right)}^{2}}}=a\xrightarrow{SHIFT-CALC}x=?.$

Chú ý:

+) M gần trung trực của AB nhất suy ra M thuộc Hypebol gần trung trực AB nhất.

+) M xa A nhất suy ra M thuộc Hypebol gần B nhất.

+) M gần A nhất suy ra M gần ${A}'$ nhất (hình vẽ) suy ra ${{k}_{{{A}'}}}\Rightarrow {{k}_{M}}.$

Dạng 4: Vị trí cực đại, cực tiểu trên đường tròn (C) đường kính AB.

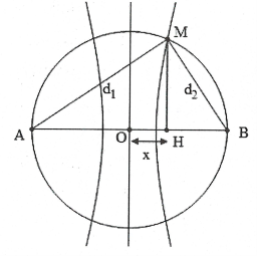
Từ giả thiết ta xác định đường Hypebol qua điểm M.

Khi đó ${{d}_{1}}-{{d}_{2}}=f\left( k \right)=a$ (đã xác định).

Suy ra ${{d}_{1}}{{d}_{2}}=\frac{d_{1}^{2}+d_{2}^{2}-{{a}^{2}}}{2}$

Lại có: $d_{1}^{2}+d_{2}^{2}=A{{B}^{2}}$ nên:

$MH=\frac{{{d}_{1}}{{d}_{2}}}{\sqrt{d_{1}^{2}+d_{2}^{2}}}=\frac{A{{B}^{2}}-{{a}^{2}}}{2AB}\Rightarrow {{d}_{1}};{{d}_{2}};x...$.

Hoặc giải hệ: $\left\{ \begin{array}{} d_{1}^{2}+d_{2}^{2}=A{{B}^{2}} \\ {} {{d}_{1}}-{{d}_{2}}=a \\ \end{array} \right.\Rightarrow {{d}_{1}};{{d}_{2}}...$

Dạng 5: Vị trí cực đại, cực tiểu trên đường tròn (C) tâm A, bán kính AB.

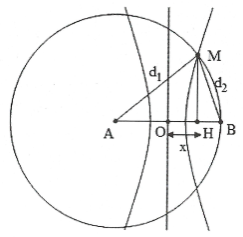
Xét điểm $M\in \left( C \right)$ tâm A bán kính R = AB.

Từ giả thiết suy ra ${{d}_{2}}-{{d}_{1}}=f\left( k \right)=a$.

Đặt OH = x ta có: $\left\{ \begin{array}{} {{d}_{2}}-{{d}_{1}}=a \\ {} {{d}_{1}}=AB \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{} {{d}_{1}} \\ {} {{d}_{2}} \\ \end{array} \right..$

$M{{H}^{2}}=d_{1}^{2}-{{\left( \frac{AB}{2}+x \right)}^{2}}=d_{2}^{2}-{{\left( \frac{AB}{2}-x \right)}^{2}}$

Giải phương trình trên tìm x.