Cách giải bài toán về lực và thời gian dãn nén con lắc lò xò (CLLX)

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1. Tổng quát:

Lực hồi phục là hợp lực có tác dụng làm vật dao động điều hòa, ${{F}_{hp}}=k\left| \left. x \right| \right.$

Lực đàn hồi là lực do lò xo bị biến dạng tác dụng lên vật, ${{F}_{dh}}=k\left| \left. \Delta l \right| \right.$

Chú ý: Trong trường hợp con lắc lò xo nằm ngang thì lực phục hồi và lực đàn hồi bằng nhau, còn ở các con lắc khác nằm ngang và thẳng đứng nó là hai đại lượng khác nhau.

1. Lực hồi phục:

Đặc điểm: luôn hướng về vị trí cân bằng.

Biểu thức tính: $F=-kx$, trong đó x là li độ

Độ lớn của lực phục hồi = Độ cứng $\times $ Độ lớn của li độ của vật: $F=k\left| \left. x \right| \right.$ nên cực tiểu bằng 0 khi qua VTCB, đạt cực đại bằng $kA$ khi qua vị trí biên.

2. Lực đàn hồi. Lực đàn hồi kéo $-$ đẩy cực đại, cực tiểu:

Lực đàn hồi là lực đưa về vị trí sao cho lò xo có chiều dài tự nhiên ${{l}_{0}}$, luôn hướng về vị trí lò xo không biến dạng( KBD).

Biểu thức vectơ: $\vec{F}=-\,k\left( \overrightarrow{\Delta {{l}_{0}}}+\vec{x} \right)$, trong đó $\overrightarrow{\Delta {{l}_{0}}}$ là độ biến dạng của lò xo khi vật ở vị trí cân bằng.

Độ lớn của lực đàn hồi = Độ cứng $\times $ Độ biến dạng của lò xo

a. Nếu con lắc lò xo bố trí nằm ngang:

$\Delta {{l}_{0}}=0$

Tại vị trí cân bằng x = 0, lực đàn hồi cực tiểu F_{đh min} = 0

Tại vị trí biên x_max = A, lực đàn hồi cực đại F_{đh max} = kA

b. Nếu con lắc lò xo bố trí thẳng đứng:

$\Delta {{l}_{0}}=\frac{mg}{k}=\frac{g}{{{\omega }^{2}}}$

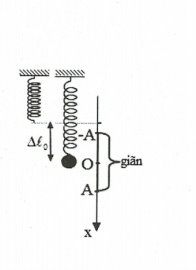
TH1: Khi $A<\Delta {{\ell }_{0}}$ khi đó lò xo chỉ dãn và không bị nén:

Độ lớn lực đàn hồi cực đại khi vật xuống thấp nhất, lò xo khi đó bị biến dạng nhiều nhất nên ${{F}_{k\acute{e}o\text{ }max}}=k\left| \left. \Delta {{l}_{0}}+A \right| \right.$.

Độ lớn lực đàn hồi cực tiểu trong trường hợp này là:

${{F}_{k\acute{e}o\text{ }\min }}=k\left| \left. \Delta {{l}_{0}}-A \right| \right.$.

TH2: Khi $A>\Delta {{\ell }_{0}}$

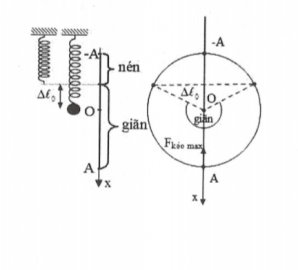
Độ lớn lực đàn hồi cực đại khi vật xuống vị trí lò xo thấp nhất, lò xo biến dạng nhiều nhất:

${{F}_{k\acute{e}o\text{ }max}}=k.\left| \left. \Delta {{l}_{0}}+A \right| \right.$ $$.

Độ lớn lực đàn hồi cực tiểu trong trường hợp này là: F_{đh min} = 0 tại vị trí lò xo không nén dãn.

Khi vật lên cao nhất, lò xo nén cực đại $$$$${{F}_{ay\text{ }max}}\,=k\left| A-\Delta {{\ell }_{0}} \right|$.

Và vì khi ${{F}_{~ay}}_{max}=k\left| \left. A-\Delta {{l}_{0}} \right| \right.<{{F}_{k\acute{e}o\text{ }max}}\,\,k.\left| \left. \Delta {{\ell }_{0}}+A \right| \right.$ nên khi lực đàn hồi cực đại chính là lực kéo cực đại tác dụng lên vật .