Cách giải bài toán về độ lệch pha

LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI.
+ Mạch chỉ có R ta có: $\varphi =0.$
+ Mạch chỉ có cuộn thuần cảm L: $\varphi =\frac{\pi }{2}.$
+ Mạch chỉ có tụ điện C: $\varphi =\frac{-\pi }{2}$
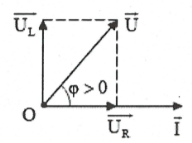
+ Mạch RL:
Ta có: $0<\varphi <\frac{\pi }{2},\left\{ \begin{array}{} \cos \varphi =\frac{R}{Z}=\frac{R}{\sqrt{{{R}^{2}}+Z_{L}^{2}}} \\ {} \tan \varphi =\frac{{{U}_{L}}}{{{U}_{R}}}=\frac{{{Z}_{L}}}{R} \\ \end{array} \right.$
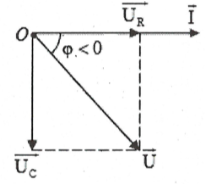
+ Mạch RC.
Ta có: $-\frac{\pi }{2}<\varphi <0,\left\{ \begin{array}{} \cos \varphi =\frac{R}{Z}=\frac{R}{\sqrt{{{R}^{2}}+Z_{C}^{2}}} \\ {} \tan \varphi =\frac{-{{U}_{C}}}{{{U}_{R}}}=\frac{-{{Z}_{C}}}{R} \\ \end{array} \right.$
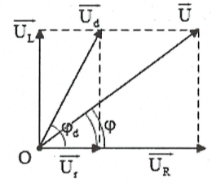
+ Mạch RLr: Ta có: $0<\varphi <{{\varphi }_{d}}<\frac{\pi }{2}.$
$\cos \varphi =\frac{R+r}{Z};\cos {{\varphi }_{d}}=\frac{r}{{{Z}_{d}}}=\frac{r}{\sqrt{{{r}^{2}}+Z_{L}^{2}}},\tan \varphi =\frac{{{Z}_{L}}}{R+r}$.
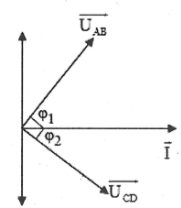
Chú ý:
+ Nếu $\overrightarrow{{{U}_{AB}}}\bot \overrightarrow{{{U}_{CD}}}\Rightarrow \tan {{\varphi }_{1}}.\tan {{\varphi }_{2}}=-1$
+ Chú ý công thức: $\tan \left( a+b \right)=\frac{\tan a+\operatorname{tanb}}{1-\tan a.\operatorname{tanb}},\tan \left( a-b \right)=\frac{\tan a-\operatorname{tanb}}{1+\tan a.\operatorname{tanb}}.$
VẬT LÝ LỚP 12
