Cách dùng vòng tròn lượng giác giải bài toán thời gian

PHƯƠNG PHÁP 1. SỬ DỤNG ĐƯỜNG TRÒN LƯỢNG GIÁC

I. LÝ THUYẾT TRỌNG TÂM VÀ PHƯƠNG PHÁP GIẢI

1. Mối liên hệ giữa dao động điều hòa và chuyển động tròn đều

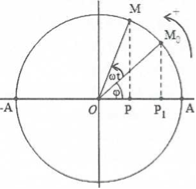
Giả sử có một điểm M chuyển động tròn đều trên một đường tròn theo chiều dương (ngược chiều kim đồng hồ) với tốc độ góc w. Gọi P là hình chiếu vuông góc của điểm M trên trục Ox trùng với một đường kính của đường tròn và có gốc trùng với tâm O của đường tròn. Ta thấy điểm P dao động trên trục Ox quanh gốc toạ độ O.

Tại thời điểm t = 0, điểm M ở vị trí M₀ được xác định bởi góc $\widehat{{{P}_{1}}OM}=\varphi (rad)$

Sau t giây, tức là tại thời điểm t nó chuyển động đến điểm vị trí điểm M xác định bởi góc $\widehat{{{P}_{1}}OM}=\omega t+\varphi (rad)$. Khi ấy tọa độ $x=\overline{OP}$ của điểm P có phương trình là $x=OM\cos \left( \omega t+\varphi  \right)=A\cos \left( \omega t+\varphi  \right)$trong đó ta có: $\omega =\frac{v}{R}$ .

Như vậy:

Một dao động điều hòa có thể được coi như hình chiếu của một chuyển động tròn đều xuống đường thẳng nằm trong mặt phẳng quỹ đạo.

Khi chất điểm chuyển động được một vòng thì vật dao động điều hòa thực hiện được một dao động. Tần số góc của hình chiếu dao động điều hòa bằng vận tốc góc của chất điểm chuyển động tròn đều đó.

Vecto vận tốc và gia tốc trên đường tròn lượng giác:

Xét góc $\varphi \in \left[ 0;2\pi  \right]$ ta có:

Khi$0<\varphi <\frac{\pi }{2}\Rightarrow \left\{ \begin{array}{} v<0 \\ {} a<0 \\ \end{array} \right.$

Khi$\frac{\pi }{2}<\varphi <\pi \Rightarrow \left\{ \begin{array}{} v<0 \\ {} a>0 \\ \end{array} \right.$

Khi$\pi <\varphi <\frac{3\pi }{2}\Rightarrow \left\{ \begin{array}{} v>0 \\ {} a>0 \\ \end{array} \right.$

Khi$\frac{3\pi }{2}<\varphi <2\pi \Rightarrow \left\{ \begin{array}{} v>0 \\ {} a<0 \\ \end{array} \right.$

Trên hình vẽ ta thấy, nếu vật chuyển động tròn đều trên nửa vòng tròn phía trên thì hình chiếu của nó âm tức là dao động điều hòa đang chuyển động theo chiều âm trục Ox, còn nếu vật chuyển động tròn đều trên nửa vòng tròn phía dưới thì hình chiếu tức dao động điều hòa sẽ đang chuyển động theo chiều dương trục Ox.

Vecoto gia tốc luôn hướng về vị trí cân bằng.

2. Phương pháp đường tròn lượng giác

BÀI TOÁN: Một vật dao động điều hòa dọc theo trục Ox với phương trình $x=A\cos \left( \omega t+\varphi \right)$. Tính khoảng thời gian ngắn nhất để vật đi từ điểm có li độ x₁ đến điểm có li độ x₂?

Phương pháp giải

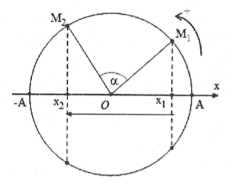
Phương trình dao động của vật có dạng $x=A\cos \left( \omega t+\varphi  \right)$

Bước 1: Vẽ trục Ox gắn vào đường tròn bán kính R = A

Bước 2: Xác định vị trí x₁ trên vòng tròn lượng giác và chiều của chuyển động.

Bước 3: Xác định vị trí x₂ trên vòng tròn lượng giác và chiều của chuyển động.

(Chiều âm nằm phía trên đường tròn, chiều dương phía dưới của đường tròn lượng giác).

Bước 4: Khi vật dao động điều hoà từ điểm x₁ đến điểm x₂ thì tương ứng trên đường tròn chất

điểm chuyển động từ M₁ đến M₂ và quét được một góc $\alpha =\widehat{{{M}_{1}}O{{M}_{2}}}$

Bước 5: Tính góc a khi đó $\alpha =\omega .\Delta t\Rightarrow \Delta t=\frac{\alpha }{\omega }$ .

Bài tập mẫu: Một vật dao động trên trục Ox với phương trình $x=4\cos \left( 2\pi t+\frac{\pi }{3} \right)cm$. Tìm khoảng thời gian ngắn nhất để vật đi từ li độ ${{x}_{1}}=2\sqrt{3}cm$ đến li độ ${{x}_{2}}=-2cm?$

Lời giải chi tiết:

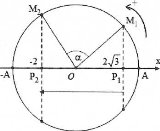
Vẽ đường tròn bán kính R = A = 4 cm.

Thời gian ngắn nhất để vật đi từ li độ ${{x}_{1}}=2\sqrt{3}cm$ đến li độ ${{x}_{2}}=-2\,cm$ là thời gian để vật đi theo 1 chiều trực tiếp (chiều âm trên hình vẽ không lặp lại hay quay vòng) từ $x=2\sqrt{3}\to x=-2$ như hình vẽ bên. Khi đó vật quét được góc $\alpha =\widehat{{{M}_{1}}O{{M}_{2}}}$ trên đường tròn lượng giác.

Ta có: $\cos \widehat{{{M}_{1}}O{{P}_{1}}}=\frac{O{{P}_{1}}}{R}=\frac{\sqrt{3}}{2}\Rightarrow \widehat{{{M}_{1}}O{{P}_{1}}}=\frac{\pi }{6}$ .

Lại có: $\cos \widehat{{{M}_{2}}O{{P}_{2}}}=\frac{O{{P}_{2}}}{R}=\frac{1}{2}\Rightarrow \widehat{{{M}_{2}}O{{P}_{2}}}=\frac{\pi }{3}$.

Do đó $\alpha =\pi -\widehat{{{M}_{1}}O{{P}_{1}}}-\widehat{{{M}_{2}}O{{P}_{2}}}=\frac{\pi }{2}$. Khi đó: $\Delta t=\frac{\alpha }{\omega }=\frac{\frac{\pi }{2}}{2\pi }=\frac{1}{4}s=0,25s$.

II. BÀI TẬP ÁP DỤNG ĐƯỜNG TRÒN LƯỢNG GIÁC CÓ LỜI GIẢI CHI TIẾT:

Lời giải chi tiết:

Ta có: v = 300 cm / s suy ra tần số góc: $\omega =\frac{v}{r}=60(rad/s)$. Chọn D

Lời giải chi tiết:

Vận tốc của vật là $v=r.\omega =4.5=20cm/s$. Chọn B.

Lời giải chi tiết:

Biên độ dao động bằng bán kính đường tròn và $A=r=\frac{v}{\omega }=\frac{50}{10}=5cm$. Chọn D.

Lời giải chi tiết:

Tần số góc: $\omega =\frac{v}{r}(rad/s)\,;\,A=r=4\,cm$

Khi P cách O một đoạn $2\sqrt{3}cm$ thì tốc độ của nó là

$\left| {{v}_{P}} \right|=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}=\frac{v}{4}\sqrt{{{4}^{2}}-{{\left( 2\sqrt{3} \right)}^{2}}}=20\left( cm/s \right)\Rightarrow v=40cm/s$ . Chọn B.

Lời giải chi tiết:

Ta có: $A=r\Rightarrow \omega r=\omega A=30={{v}_{\max P}}$ .

Lại có: ${{\left( \frac{{{x}_{P}}}{A} \right)}^{2}}+{{\left( \frac{{{v}_{P}}}{{{v}_{\max P}}} \right)}^{2}}=1\Rightarrow \frac{{{9}^{2}}}{{{A}^{2}}}+{{\left( \frac{24}{30} \right)}^{2}}=1\Rightarrow A=15cm$. Chọn B.

Lời giải chi tiết:

Ta có: $A=r=10cm,\omega =5rad/s\Rightarrow {{v}_{\max }}=\omega A=50cm/s$. Chọn B.

Lời giải chi tiết:

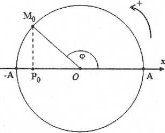
Tại thời điểm ban đầu t = 0 ta có: $\varphi =\frac{2\pi }{3}$ .

Do đó $x=4\cos \frac{2\pi }{3}=-2$ và vật đang chuyển động theo chiều âm của trục Ox

Chọn D.

Lời giải chi tiết:

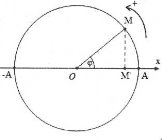
Tại thời điểm ban đầu t = 0,5s ta có: $\varphi =\frac{\pi }{6}$ .

Do đó: $x=8\cos \frac{\pi }{6}=4\sqrt{3}$ và vật đang chuyển động theo chiều âm của trục Ox. Chọn C.

Lời giải chi tiết:

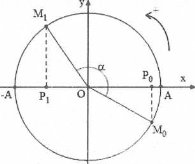
Tại thời điểm $t=0\Rightarrow {{\varphi }_{0}}=-\frac{\pi }{6}$ ứng với điểm M₀ trên vòng tròn lượng giác.

Tại thời điểm vật có li độ $x=-\frac{A}{\sqrt{2}}$ lần thứ nhất ứng với điểm M­₀ trên vòng tròn lượng giác.

Ta có: $\widehat{{{M}_{0}}O{{P}_{0}}}=\frac{\pi }{6};\widehat{{{M}_{1}}Oy}=\widehat{O{{M}_{1}}{{P}_{1}}}=\arcsin \frac{\left| {{x}_{1}} \right|}{A}=\frac{\pi }{4}$

Do đó $\alpha =\widehat{{{M}_{0}}O{{M}_{1}}}=\frac{11\pi }{12}\Rightarrow \Delta t=\frac{\alpha }{\omega }=\alpha \,.\frac{T}{2\pi }=\frac{11T}{24}$ . Chọn C.

Lời giải chi tiết:

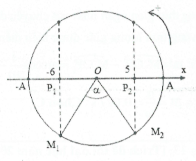
Thời gian ngắn nhất vật đi từ điểm có li độ x = - 6 cm đến điểm có li độ x = 5 cm là thời gian vật quét được góc $\alpha =\widehat{{{M}_{1}}O{{M}_{2}}}$ trên đường tròn lượng giác như hình vẽ bên.

$\begin{array}{} Ta\text{ }c\acute{o}\,:\,\,\,\cos {{\alpha }_{1}}=\cos \widehat{{{M}_{1}}O{{P}_{1}}}=\frac{6}{10}\Rightarrow {{\alpha }_{1}}=0,927rad. \\ {} \cos {{\alpha }_{2}}=\cos \widehat{{{M}_{2}}O{{P}_{2}}}=\frac{\pi }{3}. \\ \end{array}$

Do đó $\alpha =\pi -{{\alpha }_{1}}-{{\alpha }_{2}}=1,167$. Khi đó $\Delta t=\frac{\alpha }{\omega }=\frac{1,167}{4}=\frac{1}{4}s=0,292s$ . Chọn A.

Lời giải chi tiết:

Vị trí ${{x}_{1}}=-4\sqrt{3}$ theo chiều dương là điểm M₁ trên vòng tròn lượng giác.

Vị trí ${{x}_{2}}=4$ theo chiều âm là điểm M₂ trên vòng tròn lượng giác.

Thời gian ngắn nhất vật di chuyển từ x₁ đến x₂ là thời gian ngắn nhất vật chuyển động từ M₁ đến M­₂ (không lặp vòng)

Ta có: $\cos {{\alpha }_{1}}=\cos \widehat{{{M}_{1}}O{{P}_{1}}}=\frac{\sqrt{3}}{2}\Rightarrow {{\alpha }_{1}}=\frac{\pi }{6}$; tương tự ${{\alpha }_{2}}=\widehat{{{M}_{2}}O{{P}_{2}}}=\frac{\pi }{3}$ .

Do đó: $\alpha =\pi -{{\alpha }_{1}}+{{\alpha }_{2}}=\frac{7\pi }{6}\Rightarrow \Delta t=\frac{6}{\pi }=1,167$. Chọn D.

Lời giải chi tiết:

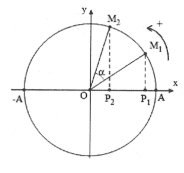
Khoảng thời gian ngắn nhất vật đi từ điểm có li độ ${{x}_{1}}=3\,cm$(ứng với điểm M₁ trên đường tròn) đến điểm có li độ ${{x}_{2}}=6\,cm$ (ứng với điểm M₂ trên đường tròn) là khoảng thời gian ngắn nhất vật chuyển động từ M₁ đến M₂ trên vòng tròn lượng giác được biểu diễn như hình vẽ bên.

Ta có $\alpha =\widehat{{{M}_{2}}O{{P}_{2}}}-\widehat{{{M}_{1}}O{{P}_{1}}}=\arccos \frac{3}{10}-\arccos \frac{6}{10}$

Suy ra $\Delta t=\frac{\alpha }{\omega }=0,027s$. Chọn C.

Lời giải chi tiết:

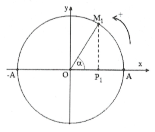
Ta có: $\left| a \right|=\frac{{{a}_{\max }}}{2}\Rightarrow \left| x \right|=\frac{A}{2}$

Tại thời điểm ban đầu $\varphi =0$ .

Như vậy thời gian ngắn nhất để gia tốc của vật bằng một nửa gia tốc cực đại bằng thời gian vật đi từ x = A đến $x=\frac{A}{2}$.

Ta có $\cos \alpha =\frac{1}{2}\Rightarrow \alpha =\frac{\pi }{3}\Rightarrow {{t}_{\min }}=\frac{\alpha }{\omega }=\frac{1}{12}\left( s \right)$ . Chọn A.

Lời giải chi tiết:

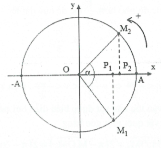
Tại thời điểm t = 0 ta có: $\varphi =-\frac{\pi }{4}\Rightarrow {{x}_{1}}=\frac{A}{\sqrt{2}}$ .

Khi $v=\frac{{{v}_{\max }}}{2}\Rightarrow {{\left( \frac{x}{A} \right)}^{2}}=1-{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=\frac{3}{4}$

Do đó $x=\pm \frac{A\sqrt{3}}{2}$ . Như vậy thời gian ngắn nhất tính từ thời điểm ban đầu đến khi vận tốc bằng một nửa tốc độ cực đại là thời gian vật đi đến vị trí $x=\frac{A\sqrt{3}}{2}$ lần thứ nhất và đang chuyển động theo chiều âm.

Khi đó vật chuyển động từ vị trí M₁ đến vị trí M₂ trên đường tròn lượng giác (hình vẽ trên)

Ta có: $\alpha =\widehat{{{M}_{1}}O{{P}_{1}}}+\widehat{{{M}_{2}}O{{P}_{2}}}=\frac{\pi }{4}+\arccos \frac{\sqrt{3}}{2}=\frac{7\pi }{24}\Rightarrow \Delta t=\frac{\alpha }{\omega }=0,104s$ . Chọn A.

Lời giải chi tiết:

Ta có: ${{\left( \frac{x}{A} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=1$ .

Theo giả thiết $\frac{v}{{{v}_{\max }}}=\frac{\sqrt{3}}{2}\Rightarrow \left| x \right|=\frac{A}{2}$ .

Thời gian ngắn nhất giữa hai thời điểm vận tốc của vật bằng $\frac{\sqrt{3}}{2}$ lần vận tốc cực đại là khoảng thời gian vật đi từ vị trí ${{x}_{1}}=\frac{A}{2}$ đến vị trí ${{x}_{2}}=-\frac{A}{2}$ hay từ điểm M₁ đến vị trí M₂ trên đường tròn lượng giác như hình vẽ (hoặc từ M₃ đến M₄) (chú ý các bạn có thể chứng minh khoảng thời gian đi từ M₄ $\to $ M­₁ hoặc M₂ $\to $ M₃ lớn hơn vì $\widehat{{{M}_{1}}O{{M}_{4}}}>\widehat{{{M}_{2}}O{{M}_{1}}}$).

Ta có: $\sin \widehat{O{{M}_{1}}{{P}_{1}}}=\frac{1}{2}\Rightarrow \widehat{O{{M}_{1}}{{P}_{1}}}=\frac{\pi }{6}$ do đó $\alpha =2\widehat{O{{M}_{1}}{{P}_{1}}}=\frac{\pi }{3}\Rightarrow t=\frac{\alpha }{\omega }=0,25\left( s \right)$

Do đó $\omega =\frac{4\pi }{3}\Rightarrow {{a}_{\max }}={{\omega }^{2}}A=175,46cm/{{s}^{2}}=1,7546m/{{s}^{2}}$. Chọn B.

Lời giải chi tiết:

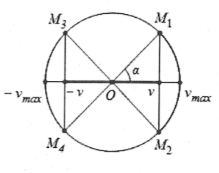
Ta có $\left| v \right|<\frac{{{v}_{\max }}}{2}\Leftrightarrow -\frac{{{v}_{\max }}}{2}<v<\frac{{{v}_{\max }}}{2}.$ Dựa vào hình vẽ ta thấy vận tốc của vật được biểu diễn bởi nét đậm. Khi đó, vật quét một góc bằng

$\begin{array}{} \Delta \varphi =2.\widehat{{{M}_{1}}O{{M}_{3}}}=2\left( \pi -\widehat{{{M}_{1}}O{{M}_{2}}} \right)=2\left( \pi -2\alpha  \right)=\frac{2\pi }{3} \\ {} \Rightarrow \Delta \varphi =\frac{2\pi }{3}\Rightarrow t=\frac{\Delta \varphi }{2\pi }.T=\frac{T}{3} \\ \end{array}$

Chọn A .