Cách chứng minh hai mặt phẳng vuông góc nhanh – bài tập có đáp án chi tiết

Cách chứng minh hai mặt phẳng vuông góc nhanh – bài tập có đáp án

Phương pháp chứng minh hai mặt phẳng vuông góc với nhau

Để chứng minh hai mặt phẳng (P) và (Q) vuông góc với nhau ta sẽ chứng minh

+ Một đường thẳng d nằm trong mặt phẳng (P) vuông góc với mặt phẳng (Q) hoặc ngược lại, một đường thằng nào đó nằm trong mặt phẳng (Q) và vuông góc với mặt phẳng (P).

+ Góc giữa hai mặt phẳng (P) và (Q) bằng 90°.

Bài tập chứng minh hai mặt phảng vuông có đáp án chi tiết

Lời giải chi tiết

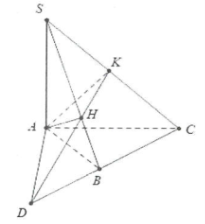
a) Do $SA\bot (ABC)\Rightarrow SA\bot BC$

Tam giác ABC vuông tại B nên $AB\bot BC$

Do đó $BC\bot (SAB)\Rightarrow (SBC)\bot (SAB)$

b) Ta có: $BC\bot (SAB)\Rightarrow BC\bot AH$

Mặt khác $AH\bot SC\Rightarrow AH\bot (SBC)\Rightarrow (AHK)\bot (SBC)$

c) Ta có: $AH\bot (SBC)\Rightarrow AH\bot SC$

Mặt khác $AK\bot SC\Rightarrow SC\bot (AHK)$ hay $SC\bot (AKD)$

Suy ra $AD\bot SC$ mà $SA\bot AD\Rightarrow AD\bot (SAC)$

Do vậy $(SAD)\bot (SAC)$

Lời giải chi tiết

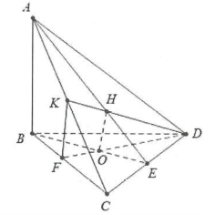
a) Ta có: $\left\{ \begin{array}  {} BE\bot CD \\  {} AB\bot CD \\ \end{array} \right.\Rightarrow CD\bot (ABE)$

mà $CD\subset \left( ADC \right)\Rightarrow \left( ADC \right)\bot \left( ABE \right)$

Lại có: $\left\{ \begin{array}  {} DF\bot BC \\  {} DF\bot AB \\ \end{array} \right.\Rightarrow DF\bot (ABC)\Rightarrow DF\bot AC$

Mặt khác $DK\bot AC\Rightarrow AC\bot (DKF)\Rightarrow (ACD)\bot (DFK)$

b) Do $CD\bot (ABE)\Rightarrow CD\bot AE$

Ta có : $\left\{ \begin{array}  {} (ACD)\bot (ABE) \\  {} (ACD)\bot (DFK) \\  {} OH=(ABE)\cap (DFK) \\ \end{array} \right.\Rightarrow OH\bot (ACD)$

Lời giải chi tiết

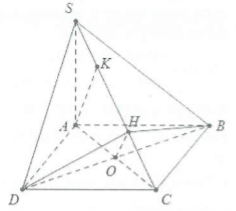
a) Do $SA\bot (ABCD)\Rightarrow SA\bot BD$

Mặt khác ABCD là hình thoi nên $AC\bot BD$

Do đó $BD\bot (SAC)\Rightarrow (SBD)\bot (SAC)$

b) Dựng $OH\bot SC$

Do $BD\bot (SAC)\Rightarrow BD\bot SC$

Suy ra $SC\bot (DHB)$

Như vậy $\widehat{DHB}$là góc giữa hai mặt phẳng (SCD) và (SBC)

Tam giác ABD đều cạnh a nên $AO=\frac{a\sqrt{3}}{2}\Rightarrow AC=a\sqrt{3}$

Dựng $AK\bot SC\Rightarrow AK=\frac{SA.OC}{\sqrt{S{{A}^{2}}+O{{C}^{2}}}}=a\Rightarrow OH=\frac{AK}{2}=\frac{a}{2}$

Tam giác DHB có đường trung tuyến$HO=\frac{1}{2}BD=\frac{a}{2}\Rightarrow \Delta DHB$ vuông tại H hay $\widehat{DHB}={{90}^{\circ }}$

Do đó $(SCD)\bot (SBC)$

Lời giải chi tiết

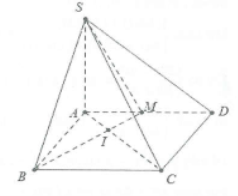
Ta có: $\tan \widehat{CAD}=\frac{CD}{AD}=\frac{a}{a\sqrt{2}}=\frac{1}{\sqrt{2}}$

Mặt khác $\tan \widehat{AMB}=\frac{AB}{AM}=\frac{a}{\frac{a\sqrt{2}}{2}}=\sqrt{2}$

Do $\tan \widehat{CAD}=\cot \widehat{AMB}\Rightarrow \widehat{CAD}+\widehat{AMB}={{90}^{\circ }}$

Suy ra $\widehat{AIM}={{90}^{\circ }}\Rightarrow AC\bot BM$tại I

Mặt khác $SA\bot (ABCD)\Rightarrow SA\bot BM$

Do đó $BM\bot (SAC)\Rightarrow (SMB)\bot (SAC)$

Lời giải chi tiết

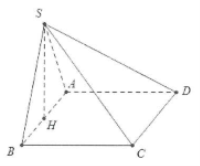
a) Do ∆SAB cân tại S nên đường trung tuyến đồng thời là đường cao suy ra $SH\bot AB$

Mặt khác $\left\{ \begin{array}  {} (SAB)\bot (ABCD) \\  {} AB=(SAB)\bot (ABCD) \\ \end{array} \right.\Rightarrow SH\bot (ABCD)$

b) Do $SH\bot (ABCD)\Rightarrow SH\bot BC$

Mặt khác $BC\bot AB\Rightarrow BC\bot (SAB)\Rightarrow \Delta SBC$vuông tại B.

c) Tương tự câu b ta chứng minh được $AD\bot (SAB)$ suy ra $(SAD)\bot (SAB)$

Mặt khác $S{{A}^{2}}+S{{B}^{2}}=A{{B}^{2}}=4{{a}^{2}}\Rightarrow \Delta SAB$vuông tại S $\Rightarrow SA\bot SB$

Lại có: $AD\bot (SAB)\Rightarrow AD\bot SB\Rightarrow SB\bot (SAD)\Rightarrow (SBC)\bot (SAD)$

Lời giải chi tiết

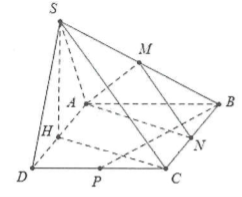
a) Gọi H là trung điểm của AD

Do ∆SAD cân tại S nên đường trung tuyến đồng thời là đường cao suy ra $SH\bot AD$

Mặt khác $\left\{ \begin{array}  {} (SAD)\bot (ABCD) \\  {} AD=(SAD)\bot (ABCD) \\ \end{array} \right.\Rightarrow SH\bot (ABCD)$

Khi đó $\left\{ \begin{array}  {} SH\bot AB \\  {} AB\bot AD \\ \end{array} \right.\Rightarrow AB\bot (SAD)\Rightarrow (SAB)\bot (SAD)$

b) Ta có: $\left\{ \begin{array}  {} MN//SC \\  {} AN//HC \\ \end{array} \right.\Rightarrow (AMN)//(SHC)$

Dễ thấy $tan\widehat{BPC}=2;\tan \widehat{HCD}=\frac{1}{2}\Rightarrow \widehat{BPC}+\widehat{HCD}={{90}^{\circ }}\Rightarrow HC\bot BP$

Mặt khác $SH\bot BP\Rightarrow BP\bot (SHC)$

Mà $(AMN)//(SHC)\Rightarrow BP\bot (AMN)\Rightarrow \left\{ \begin{array}  {} (SBP)\bot (AMN) \\  {} BP\bot AM \\ \end{array} \right.$

Lời giải chi tiết

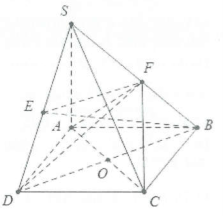
a) Ta có: ABCD là hình vuông nên $AC\bot BD$

Mặt khác $SA\bot (ABCD)\Rightarrow SA\bot BD$

Do đó $BD\bot (SAC)\Rightarrow (SBD)\bot (SAC)$

b) Ta có : $\left\{ \begin{array}  {} AD\bot AB \\  {} AD\bot SA \\ \end{array} \right.\Rightarrow AD\bot (SAB)$

Do đó $(SAD)\bot (SAB)$

c) Ta có : $AD\bot (SAB)\Rightarrow AD\bot SB$

Mặt khác $DF\bot SB\Rightarrow (ADF)\bot SB\Rightarrow AF\bot SB$

Lại có : $\left\{ \begin{array}  {} BC\bot AB \\  {} BC\bot SA \\ \end{array} \right.\Rightarrow BC\bot (SAB)\Rightarrow BC\bot AF$

Do đó $AF\bot (SBC)\Rightarrow (ACF)\bot (SBC)$

Dễ thấy tam giác SBD cân tại S có 2 đường cao BE và DF nên EF//BD

Mặt khác $BD\bot (SAC)$(Chứng minh ở câu a) suy ra $EF\bot (SAC)\Rightarrow (\text{AEF)}\bot (SAC)$

Cách khác: Ta có $AF\bot (SBC)\Rightarrow AF\bot SC$

Chứng minh tương tự ta cũng có: $AE\bot SC$ suy ra $SC\bot (AEF)\Rightarrow (SAC)\bot (AEF)$

Lời giải chi tiết

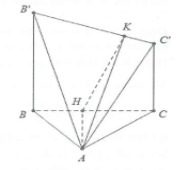
a) Ta có: $CC'\bot (ABC)\Rightarrow CC'\bot AB$

Mặt khác $AB\bot AC\Rightarrow AB\bot (ACC')\Rightarrow (ABB')\bot (ACC')$

b) Do $AH\bot BC,BB'\bot (ABC)\Rightarrow BB'\bot AH$

Suy ra $AH\bot (BCC'B')\Rightarrow (AHK)\bot (BCC'B')$

Mặt khác $AH\bot (BCC'B')\Rightarrow AH\bot B'C'$

Lại có: $AK\bot B'C'\Rightarrow B'C'\bot (AHK)\Rightarrow (AHK)\bot (AB'C')$

Lời giải chi tiết

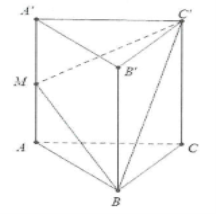
a) Ta có: ABC.A’B’C’ là lăng trụ đứng nên $BB'\bot AB$

Mặt khác ∆ABC là tam giác vuông tại B nên $AB\bot BC$

Do đó $AB\bot (BCC'B')\Rightarrow (ABB'A')\bot (BCC'B')$

$\begin{array}  {} BM=\sqrt{A{{B}^{2}}+A{{M}^{2}}}=a\sqrt{2};BC'=\sqrt{B{{C}^{2}}+CC{{'}^{2}}}=a\sqrt{7}; \\  {} C'M=\sqrt{A'C{{'}^{2}}+A'{{M}^{2}}}=a\sqrt{5} \\ \end{array}$

Do $C'{{M}^{2}}+M{{B}^{2}}=BC{{'}^{2}}\Rightarrow \Delta BMC'$ vuông tại M hay $BM\bot C'M$

b) Diện tích tam giác ABC là ${{S}_{ABC}}=\frac{{{a}^{2}}\sqrt{3}}{2}$

Diện tích tam giác MBC’: ${{S}_{MBC'}}=\frac{1}{2}MB.MC'=\frac{a\sqrt{10}}{2}$

Gọi φ là góc giữa mặt phẳng (BMC’) và mặt đáy (ABC)

Do ∆ABC là hình chiếu vuông góc của tam giác MB’C’ trên mặt phẳng (ABC) nên:

${{S}_{ABC}}={{S}_{MBC'}}cos\varphi \Rightarrow cos\varphi =\frac{{{S}_{ABC}}}{{{S}_{MBC'}}}=\sqrt{\frac{3}{10}}$