Cách Chứng minh hai đường thẳng vuông góc bằng cách chứng minh đường thẳng này vuông góc với mặt phẳng chứa đường thẳng kia.

Cách Chứng minh hai đường thẳng vuông góc bằng cách chứng minh đường thẳng này vuông góc với mặt phẳng chứa đường thẳng kia.
Phương pháp giải:
– Muốn chứng minh đường thẳng a vuông góc với đường thẳng b, ta đi tìm mặt phẳng (β) chứa đường thẳng b sao cho việc chứng minh a $\bot $ (β) dễ thực hiện.
– Sử dụng định lý ba đường vuông góc.
Bài tập về chứng minh quan hệ vuông góc trong không gian có đáp án chi tiết
| Bài tập 1: Cho tứ diện đều ABCD. Chứng minh các cặp cạnh đối diện của tứ diện này vuông góc với nhau từng đôi một. |
Lời giải chi tiết
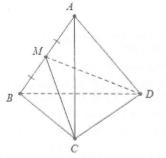
Gọi M là trung điểm của AB
Tứ diện ABCD đều nên ∆ABD và ∆ABC là các tam giác đều suy ra $\left\{ \begin{array} {} DM\bot AB \\ {} CM\bot AB \\ \end{array} \right.\Rightarrow AB\bot (MCD)$
Do đó $AB\bot CD$
Chứng minh tương tự ta cũng có $BC\bot AD,AC\bot BD$
| Bài tập 2: Hình chóp S.ABCD có cạnh SA vuông góc với mặt phẳng (ABCD) và đáy ABCD là hình thang vuông tại A và D với $AD=CD=\frac{AB}{2}$
a) Gọi I là trung điểm của đoạn AB, chứng minh $CI\bot AB$ và $DI\bot SC$ b) Chứng minh các mặt bên của hình chóp S.ABCD là các tam giác vuông. |
Lời giải chi tiết
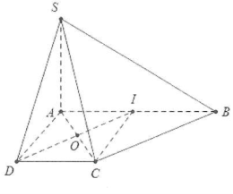
a) Đặt AB = 2a $\Rightarrow $ AD = CD = a
Do AB = 2CD $\Rightarrow $ AI = AD = CD = CI = a
Khi đó AICD là hình vuông cạnh a.
Do đó $CI\bot AB$
Mặt khác $\left\{ \begin{array} {} AC\bot DI \\ {} DI\bot SA \\ \end{array} \right.\Rightarrow DI\bot (SAC)\Rightarrow DI\bot SC$
b) Do $SA\bot (ABCD)\Rightarrow \Delta SAD,\Delta SAB$ vuông tại S.
Mặt khác $\left\{ \begin{array} {} CD\bot AD \\ {} CD\bot SA \\ \end{array} \right.\Rightarrow CD\bot (SAD)\Rightarrow CD\bot SD$
nên ∆SDC vuông tại D.
Xét ∆ACD có trung tuyến $CI=\frac{AB}{2}\Rightarrow \Delta ACD$vuông tại C$\Rightarrow BC\bot AC$
Mặt khác $BC\bot SA\Rightarrow BC\bot (SAC)\Rightarrow BC\bot SC\Rightarrow \Delta SCB$vuông tại C.
| Bài tập 3: Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh a. Cạnh bên CC’ vuông góc với đáy và CC’ = a.
a) Gọi I là trung điểm của BC. Chứng minh $AI\bot BC'$ b) Gọi M là trung điểm của BB’. Chứng minh $BC'\bot AM$ c) Gọi K là điểm trên đoạn A’B’ sao cho $B'K=\frac{a}{4}$ và J là trung điểm của B’C’. Chứng minh rằng: $AM\bot MK$ và $AM\bot KJ$ |
Lời giải chi tiết
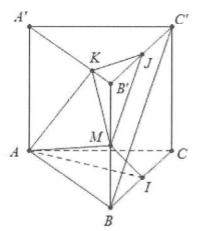
a) Do ∆ABC là tam giác đều và I là trung điểm của BC nên $AI\bot BC$
Mặt khác $AI\bot CC'\Rightarrow AI\bot (BCC'B')\Rightarrow AI\bot BC'$
b) Dễ thấy BCC’B’ là hình vuông nên $B'C\bot BC'$
Mặt khác MI là đường trung bình trong tam giác B’BC nên MI//B’C suy ra $MI\bot BC'$
Lại có: $AI\bot BC'\Rightarrow BC'\bot (AIM)\Rightarrow BC'\bot AM$
c) Ta có: $\tan \widehat{KMB'}=\frac{KB'}{MB'}=\frac{1}{2};\tan \widehat{AMB}=\frac{AB}{BM}=2$
Suy ra $\tan \widehat{KMB'}=\cot \widehat{AMB}\Rightarrow \widehat{KMB'}+\widehat{AMB}={{90}^{\circ }}$
Do đó $\widehat{AMK}={{90}^{\circ }}\Rightarrow AM\bot MK$
Mặt khác $\left\{ \begin{array} {} AM\bot BC' \\ {} MJ//BC' \\ \end{array} \right.\Rightarrow AM\bot MJ$
Suy ra $AM\bot (MKJ)\Rightarrow AM\bot KJ$
| Bài tập 4: Cho hình chóp đều S.ABCD đáy ABCD là hình vuông, gọi E là điểm đối xứng của D qua trung điểm của SA. Gọi M, N lần lượt là trung điểm của AE và BC. Chứng minh rằng $MN\bot BD$ |
Lời giải chi tiết
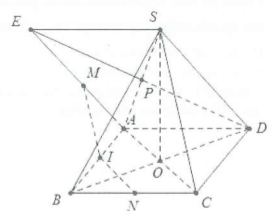
Gọi I, P lần lượt là trung điểm của AB và SA, O là giao điểm của AC và BD.
Ta có: $\left\{ \begin{array} {} IN//AC \\ {} AC\bot BD \\ \end{array} \right.\Rightarrow BD\bot IN$ (1)
Mặt khác $\left\{ \begin{array} {} IM//BE \\ {} BE\bot PO \\ \end{array} \right.\Rightarrow IM\bot PO$ (*)
Mà $PO\bot BD$ (**) (Do ∆BPD là tam giác cân tại P có đường trung tuyến PO).
Từ (*) và (**) ta có: $BD\bot IM$ (2)
Từ (1) và (2) ta có: $BD\bot (IMN)\Rightarrow BD\bot MN$
TOÁN LỚP 12
